[Paper Review]Diffusion Models Beat GANs on Image Synthesis(ADM-G)

GoodYoung included in Paper Review DL Diffusion

2025-02-28 1790 words 9 minutes

Contents

개요

GAN 대비 Diffusion Model(DM)의 이미지 생성 성능을 비교하며, DM이 GAN을 능가하는 이유를 분석한 Diffusion Models Beat GANs 논문을 리뷰할 것이다.

Introduction

요즘의 생성 모델은 많이 발전해오고 있다. 하지만 그 중에도 발전 가능성이 아직 많다.

생성 모델이 더욱 발전 한다면, 사용할 수 있는 분야가 셀 수 없이 많다.

GAN은 여러 평가 지표 (FID, Inception Score, Precision, … 등)에 의하여 image generation에서 SOTA를 달성하고 있다.

하지만 이 평가 지표는 다양성을 완전히 포착하지 않고, likelihood-based model보다 더 다양성을 포착하지 않는다.

또한, GAN은 최적의 하이퍼 파라미터와 정규화를 하지 않으면 모델이 붕괴하기 때문에 훈련이 어렵다.

이러한 GAN의 단점 때문에 다른 domain에 적용하기에도 어렵고, 확장시키기도 어려워졌다. 그 결과 likelihood-based model이 GAN의 sampling image quality와 비슷하게 발전해왔다.

likelihood-based model도 결국 단점이 있었는데, sampling 시 GAN보다 매우 느리고 sample quality 또한 기대에 미치진 못한다.

Likelihood-based model의 한 종류인 Diffusion model이 등장하여 확장성도 있고, 높은 품질을 만들어내는 성능을 보였주었다.

CIFAR-10에서 SOTA를 달성했지만 다른 어려운 dataset(LSUN, ImageNet)에 대해서는 GAN에 밀려있었다.

논문 저자들이 Improved Denoising Diffusion Probabilistic Models에서 diffusion model의 신뢰성을 증가시키는 연구를 했지만 FID가 GAN에 비하여 경쟁력 있지는 않았었다.

본 논문에선 GAN과 Diffusion model이 차이가 나는 두 가지 요인에서 비롯된다고 가정한다.

최근 GAN 연구에서 사용된 모델 아키텍처는 광범위하게 탐색되고 최적화되었다.
GAN은 다양성(diversity)과 정확성(fidelity) 사이에서 trade-off의 균형을 조절한다. 따라서 GAN은 높은 품질의 샘플을 생성하는 대신 전체 데이터 분포를 완전히 포괄하지는 못한다.
- GAN은 Generator, Discriminator로 나뉘어져 있으므로 둘 간 균형을 조정한다.

본 논문에선 이 두 가지의 요인을 Diffusion model에도 적용하고자 한다.

먼저 모델의 아키텍쳐를 개선하고, 이후 다양성과 정확성 간의 trade-off의 균형을 조절 할 수 있는 기법을 개발한다.

이 결과 본 논문에서 제안한 diffusion model이 새로운 SOTA를 달성하며, GAN을 이기게 되었다.

Background

이번 단락에서는 Diffusion model 중 DDPM에 대한 간단한 배경을 설명하고 있다. Diffusion model에 대한 자세한 설명은 해당 링크에서 보면 될 것 같다.

DDPM에서의 목표는 조금 더 덜 노이즈가 포함된 $x_\text{t-1}$ 를 $x_t$에서 생성하는 과정을 학습하게 된다.

DDPM에서 학습하기 위한 loss로 실제 변분 하한(Variational Lower Bound) $L_\text{vlb}$를 단순화한 $L_\text{simple}$이 성능이 좋음을 관찰하였다.

이런 훈련 절차와 샘플링 절차는 denoising score matching model과 동일하다고 한다.

다음으로, 조금 더 나은 diffusion model을 설명하게 되는데 기존 DDPM에서는 reverse process에서의 분산 $\Sigma_\theta(x_t, t)$ 을 고정된 값으로 설정하였는데, 이런 고정된 분산이 샘플링 단계 수가 적을 때 성능이 낮아질 수 있다.

따라서 $\Sigma_\theta(x_t, t)$ 를 파라미터화 하여 해결하려고 했고, 훈련 loss 또한 $L_\text{vlb}$ 과 $L_\text{simple}$ 를 함께 사용하는 hybrid objective로 해결한다.

본 논문에서도 해당 objecive와 parameterization을 사용한다.

또한 DDIM의 Non-Markovian 과정으로 인한 샘플링 스텝을 줄이는 방법 또한 본 논문에서 사용한다.

마지막으로 샘플 품질을 평가하는 metrics에 관한 설명으로 이어진다. Metrics 중 Inception Score(IS)는 ImageNet 클래스 분포를 얼마나 잘 학습했는지를 측정하는 메트릭이다.

개별 샘플이 특정 클래스의 예제를 얼마나 그럴듯하게 평가하면서도, 모델이 전체 dataset 클래스 분포를 잘 반영했는지 측정한다. 이런 IS도 한계점이 있는데, 아래는 IS의 한계점을 설명한 것이다.

모든 클래스에 대한 전체 분포를 얼마나 잘 커버하는지 평가하지 못한다.
데이터셋의 일부를 단순히 암기한 모델도 높은 IS 점수를 가질 수 있다.

Fréchet Inception Distance (FID)는 IS보다 더 다양성을 잘 평가할 수 있는 방법이다. Inception-V3 모델의 latent space에서 두 이미지 분포 간 거리를 측정하여 두 이미지 분포 간의 symmetric measure of distance를 측정하게 된다.

sFID라는 변형 버전은 기존 FID보다 공간적 특성을 고려하여 더 정교한 평가가 가능하다.

마지막 평가 방법인 개선된 precision & recall 기반 metrics가 있다.

본 논문은 FID를 기본 평가 지표로 사용하고 일관된 평가를 위해 동일한 공개 샘플, 코드베이스를 사용하여 평가를 진행한다.

Architecture Improvements

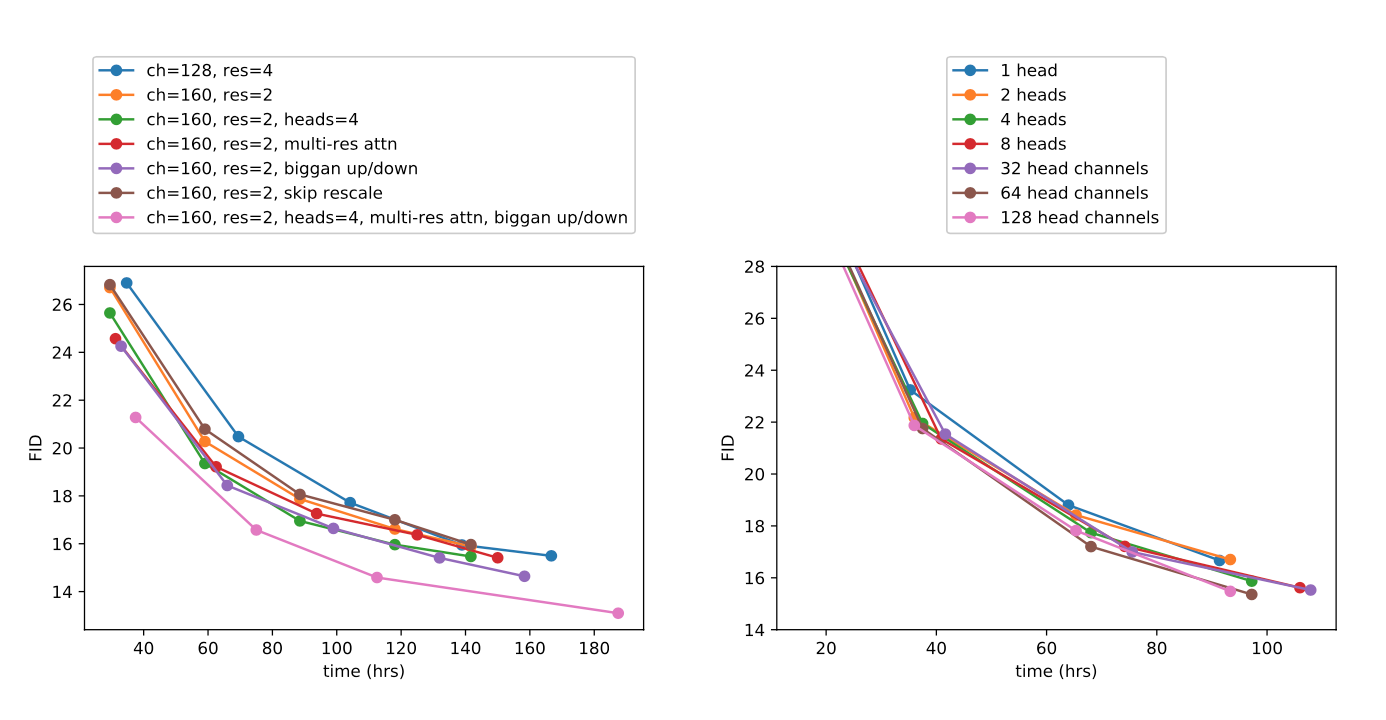
Introduction 11번 글에서 설명했듯이 모델의 아키텍쳐를 개선한 방법론을 먼저 설명을 할 것이다. 그 후 다양성과 정확성을 조절한 Classifier Guidance를 설명할 것이다.

모델의 아키텍쳐를 개선하기 위하여 모델 구조에 대하여 ablation study를 진행하였다. DDPM에서는 UNet을 사용하였고 해당 구조는 다음과 같은 구성을 가진다. 모든 실험은 동일한 데이터 셋에서 진행했다.

Residual layers와 다운샘플링 & 업샘플링 convolutions을 거쳐 피처를 압축 및 복원
Skip connections을 사용하여 같은 공간 크기(spatial size)를 갖는 레이어 간 정보를 직접 전달
16×16에서 단일 헤드를 사용하는 글로벌 어텐션(Global Attention) 레이어 추가
각 Residual block에 timestep embedding 투영(projection)

본 논문에서는 다음의 구성을 추가하여 모델 구조를 변형하여 실험한다.

깊이 vs. 너비 조정 → 모델 크기를 유지하면서 깊이를 늘릴지, 너비를 늘릴지 실험
- 깊이를 증가시키면 성능이 향상되지만, 학습 시간이 길어지는 단점이 발생
- 이후 실험에서 깊이를 증가시키는 실험을 사용하지 않기로 결정함
attention head 수 증가 → 더 많은 attention head가 성능 향상에 기여하는지 실험
- 고정된 attention head 수 vs 고정된 채널 수를 비교 실험을 하였다.
  - attention를 늘리거나 head당 채널 수를 줄이는 것이 FID 향상
attention 범위 확장 → 기존 16×16에서만 적용하던 attention을 32×32, 16×16, 8×8에도 적용
BigGAN residual block 활용 → 업샘플링 및 다운샘플링 과정에서 BigGAN의 residual block 사용
Residual connection rescaling → 안정성을 위해 residual connection을 $\frac{1}{\sqrt{2}}$ 로 rescale

결론적으로 residual connection을 rescale 하는 것을 제외하고 이러한 실험 사항들이 서로 결합될 때 더 큰 성능 향상을 보였다.

Adaptive Group Normalization(AdaGN)

AdaGN은 Group Normalization 후에 timestep 및 class embedding을 residual block에 적용하는 방식이다.

$$\text{AdaGN}(h,y) =y_s\text{GroupNorm}(h) + y_b$$

$h$: 첫 번째 convolution 이후의 residual block의 중간 활성값(intermediate activations)
$y = [y_s, y_b]$: timestep 및 class embedding을 선형 변환하여 생성된 벡터

이로 인하여 각 residual block에 timestep과 클래스 정보를 반영할 수 있음

초기에 AdaGN을 적용한 diffusion model에서 성능 향상을 하여, 기본 값으로 사용을 한다.

그래서 모든 비교 실험을 거쳐 최종 모델 아키텍쳐는 다음과 같다.

각 해상도당 residual block 2개
64채널 per head의 다중 어텐션 구조
해상도 32×32, 16×16, 8×8에서 어텐션 적용
BigGAN residual blocks을 업/다운샘플링에 사용
AdaGN 적용

Classifier Guidance

conditional gan은 잘 설계된 아키텍쳐와 함께 class labels을 활용한다. 이처럼 Class 정보가 생성 모델의 중요한 역할을 한다.

GAN에서는 discriminator를 통하여 class 정보를 반영한다.

따라서 conditional diffusion도 연구해볼만한 가치가 있다.

이미 AdaGN에서 class 정보를 포함하는 방법을 사용했는데, 이 방법 말고 본 논문은 classifier ($p(y|x)$)를 활용하여 diffusion의 성능을 향상시키는 것을 보여준다.

이전 연구에서는 pretrained diffusion model이 classifier의 gradient를 활용하여 조건부 생성이 가능함을 보였다.

따라서 본 논문은 noisy한 $x_t$를 기반으로 분류기 $p_\phi(y|x_t,t)$를 학습시키고, 그 gradient를 활용 ($\nabla_{x_t}logp_\phi(y|x_t,t)$)하여 diffusion sampling process를 특정 클래스 $y$로 유도되도록 할 것이다.

앞으로 분류기 조건부 샘플링 방법에 대해 두 가지를 검토 한 후 샘플 품질 개선에 대해서 사용하는 방법을 설명 할 것이다.

Conditional Reverse Noising Process

$$p_{\theta, \phi}(x_t \mid x_{t+1}, y) = Z p_{\theta}(x_t \mid x_{t+1}) p_{\phi}(y \mid x_t)$$

$Z$는 정규화 상수

위 식 유도

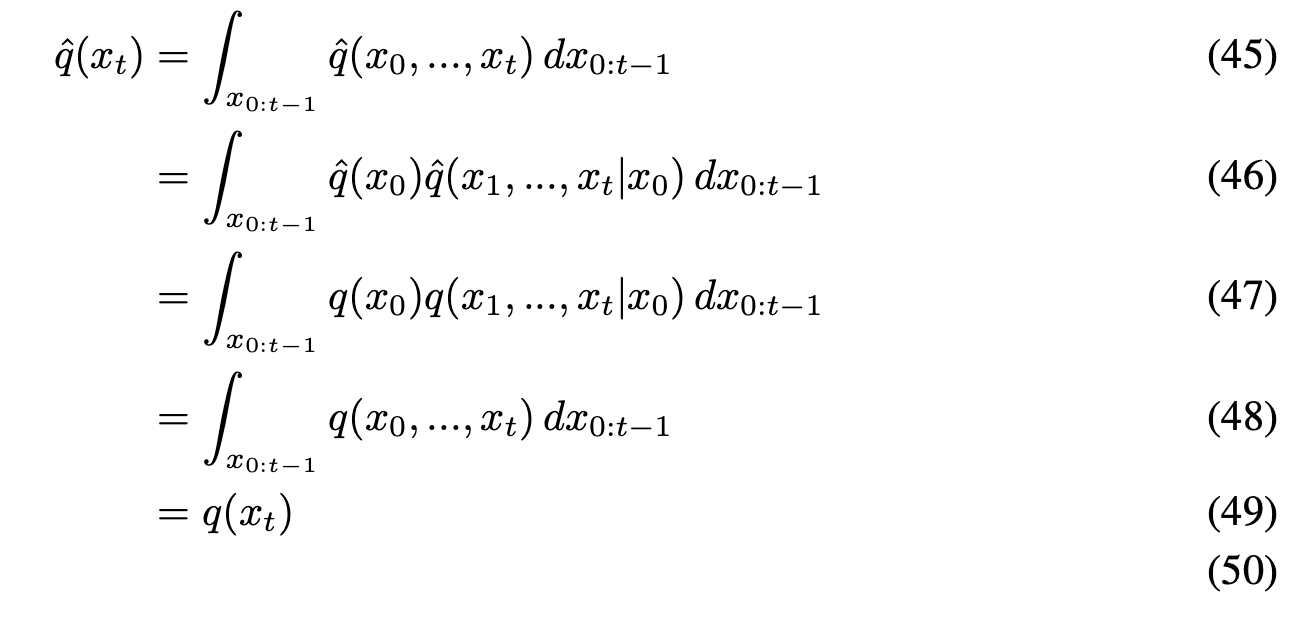
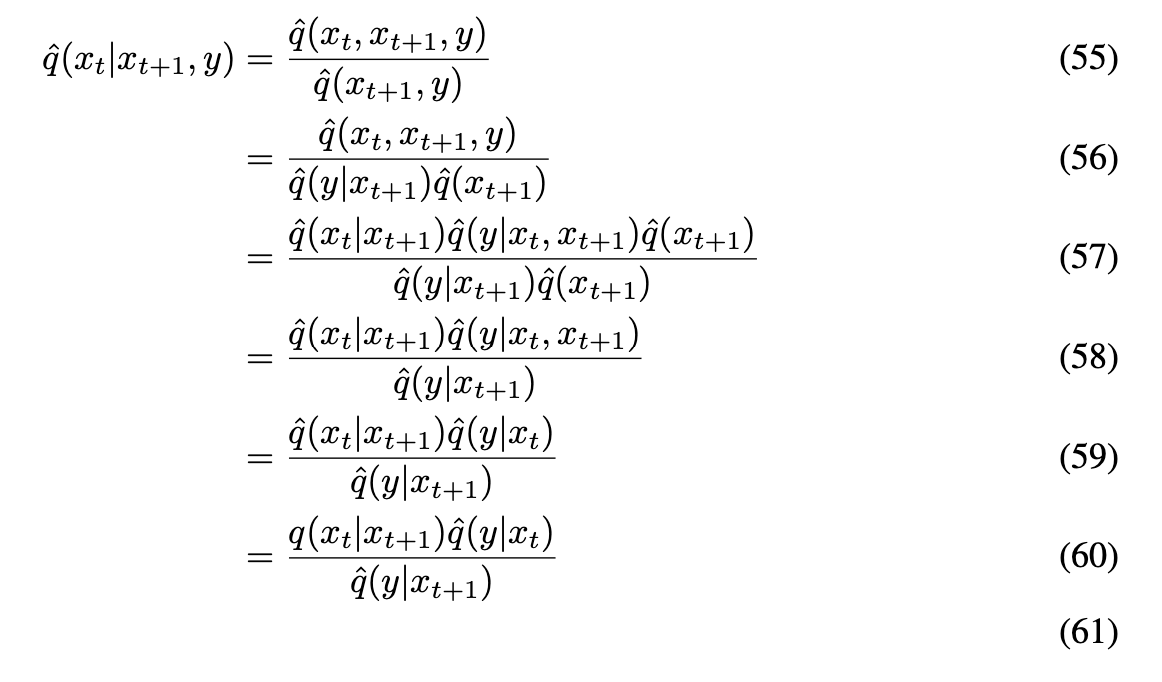
(59)에서 $\hat{q}$가 $q$가 된 이유는 (53)때문이다.
(60)에서 $\hat{q}(y \mid x_{t+1})$가 $x_t$에 영향을 받지 않으므로, 상수 ($Z$)취급이 가능하다.
해당 전개는 본 논문 Appendix H에 있는 내용을 가져온 것이다.

기존 Unconditional ddpm의 reverse process의 식은 $p_\theta(x_t|x_\text{t+1})$을 사용한다. 이를 class label $y$에 대해 condition 하게 변경한다면 위 식으로 변경이 가능하다.

$$ \begin{aligned} \log p_{\phi}(y \mid x_t) &\approx \log p_{\phi}(y \mid x_t) \Big|_ {x_t = \mu} + (x_t - \mu) \nabla_{x_t} \log p_{\phi}(y \mid x_t) \Big|_{x_t = \mu} \\ &= (x_t - \mu) g + C_1 \\ g &= \nabla _ {x_t} \log p _ {\phi}(y \mid x_t) \end{aligned} $$

따라서 $p_{\phi}$를 계산하면 sampling 식을 다시 유도 할 수 있을 것이다. 위는 $p_{\phi}$을 테일러 정리를 활용하여 전개한 것이다.

$$ \begin{aligned} \log \big( p_{\theta}(x_t \mid x_{t+1}) p_{\phi}(y \mid x_t) \big) &\approx -\frac{1}{2} (x_t - \mu)^T \Sigma^{-1} (x_t - \mu) + (x_t - \mu) g + C_2\\ &= -\frac{1}{2} (x_t - \mu - \Sigma g)^T \Sigma^{-1} (x_t - \mu - \Sigma g) + \frac{1}{2} g^T \Sigma g + C_2 \\ &= -\frac{1}{2} (x_t - \mu - \Sigma g)^T \Sigma^{-1} (x_t - \mu - \Sigma g) + C_3 \\ &= \log p(z) + C_4, \quad z \sim \mathcal{N}(\mu + \Sigma g, \Sigma) \end{aligned} $$

$p_{\phi}$과 기존 ddpm에서 나온 $p_{\theta}(x_t \mid x_{t+1})$의 식을 활용하여 위 식을 전개할 수 있다.

맨 마지막 식을 확인을 하면 $log p(z)$의 $z$는 $\mathcal{N}(\mu + \Sigma g, \Sigma)$에서 sampling이 된 것을 확인 할 수 있다.

이는 unconditional 에서 평균($\mu$)을 $\Sigma g$만큼 shift한 것이다. 따라서 $g$는 classifier의 gradient의 값이므로 이 gradient를 활용하여 conditional을 만족하게 된다.

정규분포에서 $x_t$추출
T부터 1까지 sampling 시작
t시점에서 $x_t$의 평균과 분산 계산
기존 ddpm gaussian distribution의 평균에 scaling factor * classifier gradient의 값을 shift한 분포에서 sampling
t가 1이 될 때까지 반복

위 알고리즘은 Classifier guided를 stochastic diffusion에 sampling을 과정이다. 여기의 scaling factor($s$)는 gradient scale이라는 하이퍼 파라미터이다.

Conditional Sampling for DDIM

위의 conditional sampling은 stochastic한 상황만 가능하다. 따라서 DDIM을 이용한 deterministic sampling method는 적용될 수 없게 된다.

따라서 score-based conditioning trick에 의하여 식 전개를 하게 된다. 따라서 score function이 아래가 된다.

$$\nabla_{x_t} \log q(x_t) = - \frac{\epsilon_{\theta}(x_t)}{\sqrt{1 - \bar{\alpha}_t}}$$

이 식을 활용하여 $log q(x_t,y)$를 정의할 수 있게 된다.

$$ \begin{aligned} \nabla_{x_t} \log q(x_t, y) &= \nabla_{x_t} \log q(x_t) + \nabla_{x_t} \log q(y \mid x_t) \\ &\approx -\frac{1}{\sqrt{1 - \bar{\alpha_t}}} \epsilon_{\theta}(x_t, t) + \nabla_{x_t} \log p_{\phi}(y \mid x_t) \\ -\frac{1}{\sqrt{1 - \bar{\alpha_t}}} \hat{\epsilon}(x_t) &= -\frac{1}{\sqrt{1 - \bar{\alpha_t}}} \left( \epsilon_{\theta}(x_t, t) - \sqrt{1 - \bar{\alpha_t}} \nabla_{x_t} \log p_{\phi}(y \mid x_t) \right) \\ \\ \hat{\epsilon} _ {\theta}(x_t, t) &= \epsilon_{\theta}(x_t, t) - \sqrt{1 - \bar{\alpha_t}} \nabla_{x_t} \log p_{\phi}(y \mid x_t) \end{aligned} $$

따라서 새로운 classifier-guided predictor $\hat{\epsilon_\theta}$가 도출되게 된다.

정규분포에서 $x_t$ 추출
T부터 1까지 sampling 시작
t시점에서 $\epsilon_\theta$에 classifier gradient를 반영하여 $\hat{\epsilon}$을 구함
그 값을 활용하여 기존 DDIM에서 $x_\text{t-1}$을 구하는 식으로 계산
t가 1이 될 때까지 반복

위 그림은 ddim 샘플링일 때의 샘플링 알고리즘을 나타낸다. Conditional Reverse Noising Process와 다른점은 classifier gradient를 통해 $\epsilon$ 모델 자체를 업데이트에 활용 한다는 점이다.

Scaling Classifier Gradients

Large scale generative task에 classifier를 적용시키기 위해 ImageNet을 가지고 모델 구조를 UNet의 downsampling 부분을 통해 학습 시켰다.

8*8 layer에 attention pool을 적용시켜 최종 결과를 나오게 했다.
Diffusion model에서 사용한 noise와 동일한 분포로 학습시켰다.

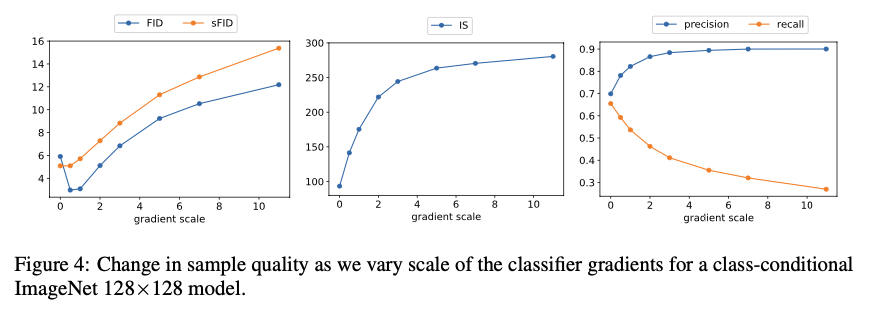
44번 줄의 샘플링 알고리즘을 보면 gradient scale의 하이퍼 파라미터가 나온다. 이것이 있는 이유는 scale = 1로 설정을 한 경우 샘플링의 결과가 class에 할당된 확률이 50% 근처이고, 1보다 큰 scale factor를 사용한 경우엔 특정 class에 속할 확률이 100% 부근의 값으로 수렴하게 된다.

위 사진을 보면 왼쪽의 scale factor = 1이고 오른쪽은 10을 사용하고, "Pembroke Welsh corgi"라는 class를 부여했을 때의 샘플링 결과이다. 결과를 보면 확실히 오른쪽의 샘플링 결과가 더욱 좋은 것을 확인할 수 있다.

수치적으로도 FID가 많이 개선이 되었다.

scale factor가 1보다 커지면 좋은 수식적인 이유

$$s \cdot \nabla_x \log p(y \mid x) = \nabla_x \log \left( \frac{1}{C} p(y \mid x)^s \right)$$

임의의 상수 $C$에 의하여 위 수식이 성립하게 된다.
따라서 s>1의 경우에 분포 $p(y|x)$는 더 sharp해지고, 이에 대한 class gradient scale을 증가한다.
s가 커질수록 특정 class에 대해 높아지고, 나머지 class에 대해서는 낮아진다.
- 이는 곧, sample의 diversity는 낮아지고, fidelity(품질)이 높아지게 된다.

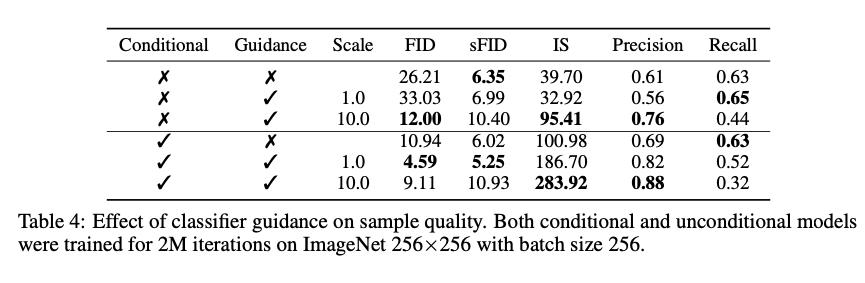
지금까지 diffusion model이 unconditional이라는 가정을 가지고 왔다. 본 논문에선 conditional diffusion model과 unconditional + classifier guidance의 FID 차이가 많이 나지 않다고 한다.

conditional model은 직접 이미지에 대한 class를 넣어주는 방식을 의미한다.

위 사진을 보면 물론, conditional model을 guided하면 FID가 더욱 향상이 되는 것을 확인 할 수 있다.

또한 위 그래프는 scale factor에 따른 평가 지표들을 비교한 그래프이다.

scale 값이 커질수록 quality (IS,precision)은 증가하지만, diversity(recall)은 감소하는 것을 확인할 수 있다.

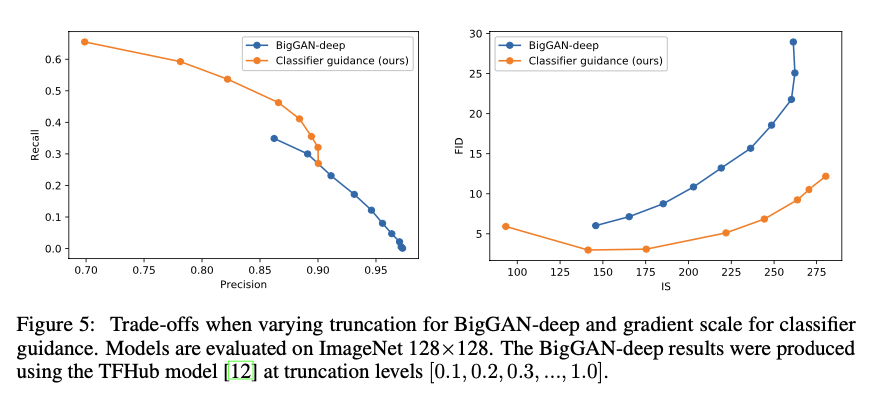
그 아래 그래프는 classifier guidance로 인해 BigGAN-deep의 성능을 뛰어 넘은 것을 확인 할 수 있다.

Results

본 논문이 제안하는 모델은 Ablated Diffusion Model(ADM)이고 classifier guidance를 사용하면 (ADM-G)이다.

다양한 데이터셋 및 해상도에서 GAN을 뛰어넘는 우수한 성능을 보여준다.

위 결과는 BigGAN-deep 모델과 제일 좋은 성능의 ADM의 sampling 이미지들이다. 대게 이미지의 quality는 비슷하지만 ADM이 더 다양한 이미지를 만들어내는 것을 확인할 수 있다.

Limitations and Future Work

여전히 denoising step을 사용하기 때문에 샘플링에서 GAN보다 느리다.

Single step model의 샘플은 이전 likelihood-based model보다는 좋고, GAN과 경쟁력은 아직 없다.

또한 이때는 classifier guidance는 레이블이 있어야 사용이 가능한 한계를 가지고 있다.

Unlabeled data로 확장이 가능하다.