[CS236] 6. Latent Variable Models-2

개요

0. 이번 포스트에서는 CS236 강의의 6강 내용과 7강의 앞부분을 설명한다.

• 7강에 VAE 내용이 포함이 되었기 때문이다.

1. 지난 포스트에서 Latent Variable Model에서 z라는 latent variable이 여러개 있을 때 Mixture of Gaussian이 된다는 점, 그 수많은 분포에서 x의 값을 구하는 방법(marginal likelihood) 등에 대해서 배웠고 그 분포를 최적화 하는 과정에서 Evidence Lower Bound(ELBO) 개념이 나오게 되었다.

2. ELBO 개념이 나오면서, 수식들을 전개했는데 이어서 설명하겠다.

---

Evidence Lower Bound(ELBO) - 2

$$ \begin{aligned} \log p(x; \theta) &\geq \sum_{z} q(z) \log \left( \frac{p_\theta(x, z)}{q(z)} \right) \\ &= \sum_{z} q(z) \log p_\theta(x, z) - \sum_{z} q(z) \log q(z) \\ &= \sum_{z} q(z) \log p_\theta(x, z) + H(q) \ \text{(H(q) is entropy)} \\ \end{aligned} $$ $$ \begin{aligned} &\text{Equality holds if } q = p(z \mid x; \theta)\\ &\log p(x; \theta) = \sum_{z} q(z) \log p(z, x; \theta) + H(q) \end{aligned} $$

3. 지난 포스트에서 위 식이 나오게 된 이유를 간단하게 정리해보겠다. 우리는 latent variable z를 직접 관측할 수 없기 때문에, 이를 추론하기 위하여 보조의 분포 q를 도입했다. 이때 x는 관측할 수 있는 부분이고 z는 보이지 않는 부분이다. 이 상황에서 우리는 x만 관찰될 때 z 분포를 근사하고자 하며, 이 과정에서 $logp(x)$ 를 직접 계산하기 어렵기 때문에, 이 식을 최적화 가능한 ELBO 식이 등장하게 나오게 된 것이다.

4. 이제 본론으로 넘어와서, 2번째 식을 살펴보자면 $\sum_{z} q(z) \log p_\theta(x, z)$ 이 항은 q모델을 사용하여 z부분을 추론할 때 x,z 부분이 모두 관찰될 떄의 평균 로그 확률이다. (모든 것이 관찰된다. 이는 본질적으로 생성 모델이다.) $\sum_{z} q(z) \log q(z)$ 이 항은 q함수이고, q의 entropy라고 볼 수 있다. (q가 얼마나 무작위적인지 알려주는 양이다.)

$$D_{\mathrm{KL}}(q(z) \parallel p(z \mid x; \theta)) = - \sum_{z} q(z) \log p(z, x; \theta) + \log p(x; \theta) - H(q) \geq 0$$

5. 이제 Equality 부분을 설명할 것이다. KL 식을 전개하면 위와 같은 식을 얻을 수 있는데 오른쪽 항에서 $\log p(z, x; \theta)$ 만 남기고 다 넘기면 ELBO의 식과 동일해지는 것을 확인할 수 있다.
   • 그렇다면 어떻게 전개를 하면 위와 같은 식이 나왔을까?
   • KL의 값은 항상 0보다 크거나 같다의 성질을 이용한다.
   • 그 후, 기존 KL의 식에서 $p(z \mid x; \theta)$ 을 Bayes 정리를 활용해서 $p(z \mid x; \theta) = \frac{p(x, z; \theta)}{p(x; \theta)}$ 로 변형하여 식 전개하면 위와 같은 식이 나온다.

6. 그렇기 때문에 만약 $ q = p(z \mid x; \theta)$ 라면 KL의 값이 0이 되기 때문에 부등식이 등식이 되는 것이다.

7. 하지만 우리는 $p(z|x;\theta)$가 계산이 불가능하다는 것을 안다.
   • GMM (lecture 5 12-17)에서 심층 가우시안 분포를 사용해 $p_\theta(x|z)$ 는 z의 분포가 정해져 있었기 때문에 구할 수 있었다. (lecture 5 16)
   • 하지만 $p(z|x;\theta) = \frac{p(z)p_\theta(x|z)}{p_\theta(x)}$ 이기 때문에, $p(x)$ 를 구할 수 없다.(lecture 5 23)
   • 따라서 $p(z|x;\theta)$ 도 계산이 불가능하다. 사실 따지고 보면 만약 posterior가 계산이 가능했으면 위 ELBO식도 필요가 없다.

8. 결국, q분포가 $p(z \mid x; \theta)$에 최대한 가까운 q를 선택해야 하는 것을 알 수 있다. 이는 앞으로 나올 Variational Inference의 이론적 도구로써 작용이 될 것이다.
   • 정리하자면 추정이 불가능한 분포를 근사하는 q를 두어 이 분포를 최적화하여 가장 강력한 lower bound를 찾는 것이 최종 목표인 것이다.
   • 따라서 q의 역할을 하는 별도의 신경망을 두고, p와 q를 공동으로 최적화하여 ELBO를 최대화 시킨다.
   • 조금 더 나아가, VAE의 인코더는 q가 되고 디코더는 p가 된다.

---

Variational Inference

9. Variational Auto Encoder(VAE) 모델에서는 decoder인 $p(x|z) = \mathcal{N}(\mu_\theta(z), \Sigma_\theta(z))$ 의 neural network가 있으면 이것을 뒤집은 encoder의 역할을 하는 $p(z|x;\theta)$ 를 계산하여 x가 주어지고 이 x를 생성할 가능성이 높은 z를 찾으려고 한다. 하지만 확률 모델을 단순히 뒤집는 것이 쉬운 문제는 아니다. 따라서 이를 해결하기 위한 방법은 지금까지 우리가 배워왔던 방법을 이용하면 된다.

10. 우리는 ELBO식을 보면서 계산 불가능한 식을 보조 분포를 정의하여 계산 불가능한 식의 분포를 근사하여 추론하는 방법을 배웠다.

11. 따라서 이를 적용하기 위하여 우리는 latent variable z에 대한 분포군을 정의할 것이다. 분포 q를 아래와 같이 정의할 수 있다.
    • $q(z;\phi) = \mathcal{N}(\phi_1, \phi_2)$
    • variational parameter $\phi$ 의 집합을 통해 매개변수화될 것이다.
    • 이를 활용하여 ELBO를 활용하여 q와 p 모두 공동으로 최적화 하려고 한다.

12. 바로 이 내용이 Varaiational Inference이다. 반복해서 정리하자면, 우리가 알고있지만 계산하기 어려운 posterior 분포를 대신하여 추론 가능한 분포 q를 도입하고 이를 최대한 가깝게 근사하게 시도하는 방법이다.

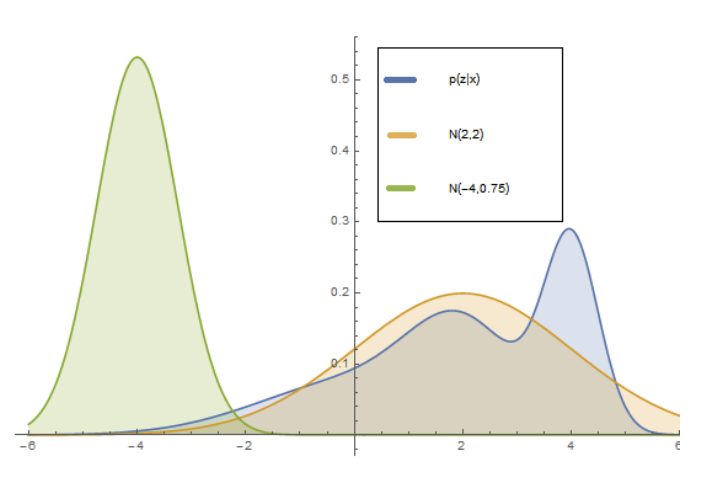
13. 좀 더 간단하게 시각화를 통하여 이해해보면, 파란색: p(z|x) 분포가 있으면, 이것에 최대한 비슷한 가우시안 분포를 찾으려고 하는 것이다. 이걸 vae 관점으로 생각해보면 비슷한 가우시안 분포를 찾을 때 parameter $\phi$ 를 사용하여 최적화 하는 것이다.

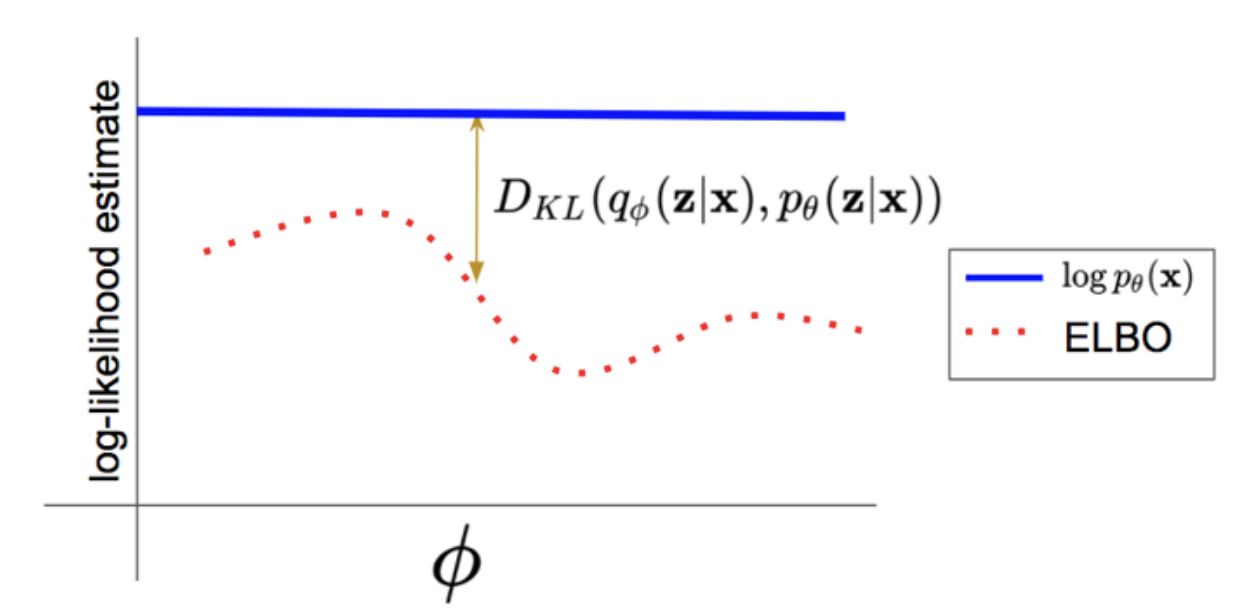
$$ \begin{aligned} \log p(\mathbf{x}; \theta) &\geq \sum_{z} q(z; \phi) \log p(z, \mathbf{x}; \theta) + H(q(z; \phi)) = \mathcal{L}(\mathbf{x}; \theta, \phi) \quad \text{(ELBO)} \\ \log p(\mathbf{x}; \theta) &= \mathcal{L}(\mathbf{x}; \theta, \phi) + D_{KL}(q(z; \phi) \parallel p(z \mid \mathbf{x}; \theta)) \end{aligned} $$

14. Variational Inference를 하면 p와 q의 공동의 조합으로 ELBO를 최적화를 할 것이다. 일단 위 수식을 살펴보면 $\log p(\mathbf{x}; \theta) $ 는 ELBO와 KL-Divergence의 합친 것으로 확인 할 수 있고 (4번 수식 참고) 따라서 $\theta$ 와 $\phi$ 으로 해당 표현식을 최적화 하는 것을 확인할 수 있다.

15. 지금까지는 단일 데이터셋 x에 대해서만 수식을 설명했다. 이제 모든 데이터셋 ($\mathcal{D}$)에 적용시켜 볼 것이다. 수식은 아래와 같다.
    • 수식을 확인하면 기존 $\log p$ 에 대하여 $\phi$ 를 사용하여 ELBO를 지정한 것을 확인할 수 있다.

$$\ell(\theta; \mathcal{D}) = \sum_{x^i \in \mathcal{D}} \log p(x^i; \theta) \geq \sum_{x^i \in \mathcal{D}} \mathcal{L}(x^i; \theta, \phi^i)$$

$$\max_{\theta} \ \ell(\theta; \mathcal{D}) \ \geq \ \max_{\theta, \phi^1, \cdots, \phi^M} \ \sum_{x^i \in \mathcal{D}} \mathcal{L}(x^i; \theta, \phi^i)$$

16. 이때 생각해야할 점이 있다. 전체 데이터셋이기 때문에, 각 데이터 포인트 ($x^i$) 마다 posterior($\log p$)가 다른 분포로 나타나야한다. 그렇기 때문에 식을 자세히 확인하면 $\phi^i$ 로 나타나있는 것을 확인할 수 있다.
    • $x^i$ 에 대해 가장 posterior에 근접한 elbo를 찾은 다음, 이 파라미터들을 공동으로 최적화한다.
    • $\theta$ 가 모든 데이터 포인트에서 공통적이더라도, 추론하는 잠재 변수의 값은 달라야한다.
      • 데이터 포인트 $x^i$ 마다 잠재 변수는 다를 것이기 때문이다.
      • 그럼 최적의 잠재 변수 분포 $q(z|x^i ; \phi^{i,*})$ 가 나오면 $\theta$ 는 공통된 decoder이기 때문에, 어떤 z에 대해서든지 x를 생성해낼 수 있어야 한다.

---

Stochastic Variational Inference (SVI)

17. 그렇다면 이 $\mathcal{L}(\mathbf{x}^i; \theta, \phi^i)$ (ELBO)식을 이제 풀어볼 시간이 왔다.

18. 해당 목적식을 훈련때 최적화 하기 위해서, 우리가 배운 방법 중 하나는 목적 함수(ELBO)에 대해 gradient descent을 하는 것이다. (참고: lecture 4 17-19)

19. 그렇다면 gradient descent의 순서를 보자.

    • $\theta,\phi^1, \phi^2, \cdots, \phi^M$: 랜덤 초기화

    • $\mathbf{x}^i \sim \mathcal{D}$ 에서 데이터 포인트 무작위 선택

    • $\mathcal{L}(\mathbf{x}^i; \theta, \phi^i)$ 식을 학습해 $\phi^i$ 를 $\phi^{i,*}$ 으로 최적화 (이때 $\theta$ 는 고정):

      • $\phi^i \leftarrow \phi^i + \eta \nabla_{\phi^i} \mathcal{L}(\mathbf{x}^i; \theta, \phi^i)$ 으로 gradient update
      • 위 과정을 반복하여 $\phi^{i,*} \approx \arg\max_{\phi} \mathcal{L}(\mathbf{x}^i; \theta, \phi)$ 로 수렴

    • $\phi^{i,*}$ 를 가지고 $\theta$ 에 대해 최적화 (실제 decoder 최적화):

      • $\nabla_\theta \mathcal{L}(\mathbf{x}^i; \theta, \phi^{i,})$ 으로 기울기 계산
      • 파라미터 업데이트: $\theta_{t+1} = \theta_t + \alpha_t \nabla_\theta \mathcal{L}(\mathbf{x}^i; \theta, \phi^{i,})$
      • 위 과정을 $t \to T$ 까지 반복하여 θ의 최적값에 수렴

20. $\phi$ 를 먼저 업데이트 하고 그다음 $\theta$ 에 대해서 업데이트를 한다. 그럼 이 기울기들을 어떻게 계산하는지 보기 위하여 목적 함수 ($\mathcal{L}(x^i; \theta, \phi^i)$) 를 조금 더 확장해보자.
    • 하지만 파라미터를 공동으로 최적화 하기 때문에, 만약 $\phi$의 최적화 방향이 안좋다면 non-convex하기 때문에 해당 목적 함수가 매우 나쁜 local minimum에 갇힐 위험은 있다.

$$ \begin{aligned} \mathcal{L}(x^i; \theta, \phi^i) &= \sum_{z} q(z; \phi^i) \log p(z, x^i; \theta) + H(q(z; \phi^i)) \\ &= \mathbb{E_{q(z; \phi^i)}} \left[ \log p(z, x^i; \theta) - \log q(z; \phi^i) \right] \end{aligned} $$

• Entropy 식(H)을 풀고, $\sum$ 과 $q(z;\phi^i)$ 를 Expectation으로 묶으면 해당 식이 된다.

21. 위 식을 보면 기울기를 계산하기 위하여 기대값과 기울기를 계산하는데 사용할 수 있는 표현식이 없다. 그렇기 때문에 다시 Monte Carlo sampling에 의존해야한다. 위 기대값을 Monte Carlo를 사용하면 $q(\mathbf{z}; \phi)$ 분포에서 $\mathbf{z}^1, \dots, \mathbf{z}^K$ 로 sampling을 하여 식을 closed-form으로 변경할 수 있다.

• K의 값이 증가할수록 값이 기대값에 가까워진다. 하지만 실제 VAE는 K의 값을 1로 선택을 했다.

$$\mathbb{E}_{q(\mathbf{z}; \phi)}\left[ \log p(\mathbf{z}, \mathbf{x}; \theta) - \log q(\mathbf{z}; \phi) \right] \approx \frac{1}{K} \sum_k \left( \log p(\mathbf{z}^k, \mathbf{x}; \theta) - \log q(\mathbf{z}^k; \phi) \right)$$

• $\log q$ 에서 q의 확률을 평가하기 때문에 효율적으로 평가해야하는 모델이어야 한다. 따라서, q의 분포는 단순해야하는 가정이 있어야한다.

22. 자, 이제 gradient descent 순서(19번)에서 2개의 gradient($\theta$, $\phi$)를 계산해보자. 먼저 $\theta$ 에 대해서 gradient를 해보면, 이미 다 나온 값들이기 때문에 Monte Carlo를 이용하여 계산하기 쉽다. 이때, 이미 다 나온값의 의미에서 $\phi$ 도 이미 고정된 분포에서 sampling을 하기 때문에 우리가 알고있는 neural network의 gradient descent라고 생각하면 된다. 따라서 $\theta$ 의 식은 아래와 같다.

$$ \nabla_\theta \mathbb{E_{q(z; \phi)}} \left[ \log p(z, x; \theta) - \log q(z; \phi) \right] = \mathbb{E_{q(z; \phi)}} \left[ \nabla_\theta \log p(z, x; \theta) \right] \approx \frac{1}{K} \sum_k \nabla_\theta \log p(z^k, x; \theta)$$

• $\theta$ 에 대해서 기울기를 구하기 때문에 $\phi$ 는 미분하면 사라진다.

23. 하지만 $\phi$ 에 대해서 gradient를 계산해보려고 하면 $\phi^i$ 에 따라 달라지는 분포에서 표본을 추출하기 때문에 기울기를 구하는데 어려움이 있다.

    • $\theta$에 의존하는 분포에서 표본을 추출하지 않기 때문에 $\theta$ 의 gradient는 구하기 쉽다.

    • 하지만, $\phi$를 변경하면 sampling 절차가 $\phi$에 따라서 어떻게 변할지 이해해야해서 어렵다.

    • $\phi$ 에 대해서 gradient 계산이 어렵다는 이해를 돕기 위해 SVI의 원형의 pseudo code가 있다.

        for _ in range(N):
            theta optimization
            for i in range(M):
                phi optimization
      
        ## Total Optimization Steps : N x M
      

    • 이 예시는 $\phi$를 최적화 하기 위해 매번 최적의 $\phi^{i,*}$ 를 구해야하는 복잡함을 단번에 이해할 수 있을 것이다.

    • 하지만 왜 그럼 $\theta$ 에 대해서는 $\theta^{i,*}$ 을 구하지 않는걸까?라는 의문은 16번을 다시 돌아가면 해결이 된다.

24. 따라서, VAE에 SVI를 적용시킬 때 2가지 문제가 있는 것이다. 첫번째는 $\phi$ 의 gradient를 계산할 때 $\phi$ 에서 샘플링을 하기 때문에 gradient 계산이 불안정하다는 점이고, 두 번째는 $\phi$ 계산이 M 번 수행되어야 된다는 점이다. 이 두 문제를 해결하기 위하여 각각 Reparameterization Trick과 Amortized Inference 방법으로 해결할 수 있다.

---

Reparameterization Trick

25. 먼저 Reparameterization Trick에 대한 개념을 살펴보고, 우리의 VAE 식 ELBO에 적용시켜 보겠다. 그리고 Reparameterization Trick을 사용하기 위한 제약사항이 있는데, 바로 잠재 변수 z가 연속일때만 작동한다는 점이다.

$$\mathbb{E_{q(z; \phi)}} \left[ r(\mathbf{z}) \right] = \int q(\mathbf{z}; \phi) , r(\mathbf{z}) , d\mathbf{z}$$

26. 그렇기 때문에 위 식을 보면 $\sum$ 이 아니라 적분으로 계산이 된다. 이제, 중요한 것은 $\phi$ 의 gradient 를 구할 때, 해당 식(ELBO)이 본질적으로 가능한 한 커지도록 $\phi$ 를 변경하는 방법을 알아내는 것 이기 때문에, 기대값 안의 식들을 $r$ 로 대체했다.
    • 이는 강화학습하고도 연관을 지을 수 있는데, z가 행동이라면 이 행동을 선택하는데 확률적인 정책(q)가 있어서 다른 행동(z)은 다른 정책(q)을 받을 수 있다.
    • 그래서 위 식을 다시 해석하면, 최대한 높은 보상(r or 기대값 전체)을 얻으려면 확률적으로 어떤 행동(z)을 선택해야 할까요? 라고 볼 수 있다.

27. 그리고 q함수를 간단한 가우시안 분포의 성격을 띈다면 $q(\mathbf{z}; \phi) = \mathcal{N}(\mu, \sigma^2I)$ 일 때 $\phi = (\mu, \sigma)$ 이다. q함수의 샘플링의 방법은 아래 2가지 방법이 될 수 있다.
    • 직접 샘플링: $\mathbf{z} \sim q(\mathbf{z}; \phi)$
    • Reparameterization Trick: $\boldsymbol{\epsilon} \sim \mathcal{N}(0, I), \quad \mathbf{z} = \mu + \sigma \odot \epsilon = g(\epsilon;\phi)$
      • Reparameterization Trick을 사용하게 되면 $\epsilon$ 의 분포가 고정이 되어 분산이 튀는 현상을 방지할 수 있게 된다.

28. 따라서 Reparameterization Trick 을 사용하게 되면 z를 결정론적 수식으로 변환을 할 수 있게 된다. 샘플링의 두가지 방법으로 인하여 기대값 계산 또한 두가지 방법이 될 수 있다.

$$\mathbb{E_{z \sim q(z; \phi)}} [r(z)] = \int q(z; \phi) r(z), dz = \mathbb{E_{\epsilon \sim \mathcal{N}(0, I)}} [r(g(\epsilon; \phi))]$$

29. 해당 수식을 보면 q에서 샘플링하여 얻은 z를 사용하여 r에서 평가하는 방법과(2번째 항)$\epsilon$ 에서 샘플링 을 한 다음, g함수로 변환을 하고 r의 기대값을 얻는 방법(3번째 항)이 있다.

30. 이제 3번째 항이 reparameterization trick으로 인하여 결정론적으로 변했기 때문에, $\phi$ 의 gradient를 조금 변경했을 때 샘플이 어떻게 변하는지 알 수 있게 도;었다.. 그렇기 때문에 gradient를 내부에 넣어서 계산이 가능해진다. 또한 위에서 22번과 마찬가지로 Monte Carlo를 다시 사용할 수 있게 되었다.

$$\nabla_{\phi} \mathbb{E_{q(z; \phi)}} [r(z)] = \nabla_{\phi} \mathbb{E_{\epsilon}} [r(g(\epsilon; \phi))] = \mathbb{E_{\epsilon}} [\nabla_{\phi} r(g(\epsilon; \phi))]$$

$$\mathbb{E_{\epsilon}} [\nabla_{\phi} r(g(\epsilon; \phi))] \approx \frac{1}{K} \sum_k \nabla_{\phi} r(g(\epsilon^k; \phi)) \quad \text{where } \epsilon^1, \dots, \epsilon^K \sim \mathcal{N}(0, I)$$

31. 이제 reparameterization trick 방법을 VAE ELBO에 적용시킬려고 보니, 단순히 $r(z)$가 아닌 $r(z, \phi)$ 인것을 확인할 수 있다. 하지만 이는 큰 문제가 되지 않는다. 아래의 식에서 확인해보자.

---

Amortized Inference

32. 이제, VAE ELBO의 gradient를 계산하는 방법을 배웠다. 하지만 아직도 문제가 있다. 바로 데이터 포인트($x^i$)당 variational parameter($\phi^i$) 가 있는 것은 M번의 수행이 이루어 져야한다는 것이고, 이는 계산 비용이 많이 든다고 생각할 수 있다.

33. 이 계산 비용을 최적화 하기 위하여, 우린 모든 $\phi$ 에 대해 개별적으로 최적화하지 않을 것이다. 대신에, 우리는 또다른 신경망이 될 단일 매개변수 세트($f_\lambda$, VAE의 encoder가 된다.)를 정의한다. 이 $f_\lambda$ 는 좋은 variational parameter를 추측하려고 시도할 것이다.
    • $x^i$ 에 걸맞는 $\phi^{i,*}$ 를 찾는 역할이라고 생각하면 될 것 같다.

$$ q_{\lambda}(z \mid x^i) \equiv q(z \mid x^i; \phi^i = f_{\lambda}(x^i))$$

• $q(z|x^i ; \phi^{i,*})$ 기존 q의 함수에서 $\phi$ 를 inference하는 $f_\lambda$ 가 나온 것을 확인할 수 있다.

34. Amortized Inference를 사용하면 이제 매개변수의 수가 고정되어 있기 때문에, 확장성이 훨씬 뛰어나지게 된다. 또한 훈련 관점에서 생각해보면 약간 헷갈릴수도 있는데, Amortized Inference를 사용하면 Encoder와 Decoder가 ELBO를 통해서 공동으로 최적화 되기 때문에 학습 파라미터에서 $\phi$ 는 없어지고, $\lambda, \theta$ 만 남게 된다.

35. VAE에서 notation을 $q(z; f_\lambda(x^i))$ 이 $q_\phi(z|x)$ 로 표기된다. 따라서 $q_\phi(z|x)$ 을 사용하여 ELBO를 다시 표기해보면 아래와 같다. 기존 ELBO 식은 20번에 있으니 비교해서 보면 좋을 것 같다.

$$ \begin{aligned} \mathcal{L}(\mathbf{x}; \theta, \phi) &= \sum_{z} q_{\phi}(z \mid \mathbf{x}) \log p(z, \mathbf{x}; \theta) + H(q_{\phi}(z \mid \mathbf{x})) \\ &= \mathbb{E_{q_{\phi}(z \mid \mathbf{x})}} \left[ \log p(z, \mathbf{x}; \theta) - \log q_{\phi}(z \mid \mathbf{x}) \right] \end{aligned} $$

• 반복해서 말하지만 $q_\phi$ 는 x를 입력으로 받아서 variational posterior 를(x에 맞는 $\phi$ 를 찾는 역할) 만드는 역할을 한다.

36. Amoritized Inference를 사용하여 gradient descent의 순서를 살펴보자.

    • $\theta^{(0)},\ \lambda^{(0)}\ \text{랜덤 초기화}$

    • $x^i \sim \mathcal{D}$

      • 전체 데이터셋 $\mathcal{D}$에서 무작위로 하나의 데이터 포인트 $x^i$를 샘플링

    • $\nabla_\theta \mathcal{L}(x^i; \theta, \lambda),\quad \nabla_\lambda \mathcal{L}(x^i; \theta, \lambda)$

      • $\phi^i = f_\lambda(x^i)$를 통해 variational 분포 $q_\phi(z|x^i)$를 정의하고, reparameterization trick을 활용해 $\theta, \lambda$ 각각에 대한 gradient를 계산

    • $\theta \leftarrow \theta + \alpha \nabla_\theta \mathcal{L}, \quad \lambda \leftarrow \lambda + \alpha \nabla_\lambda \mathcal{L}$

      • optimizer (예: Adam)를 사용하여 $\theta$와 $\lambda$를 업데이트

---

Autoencoder Perspective

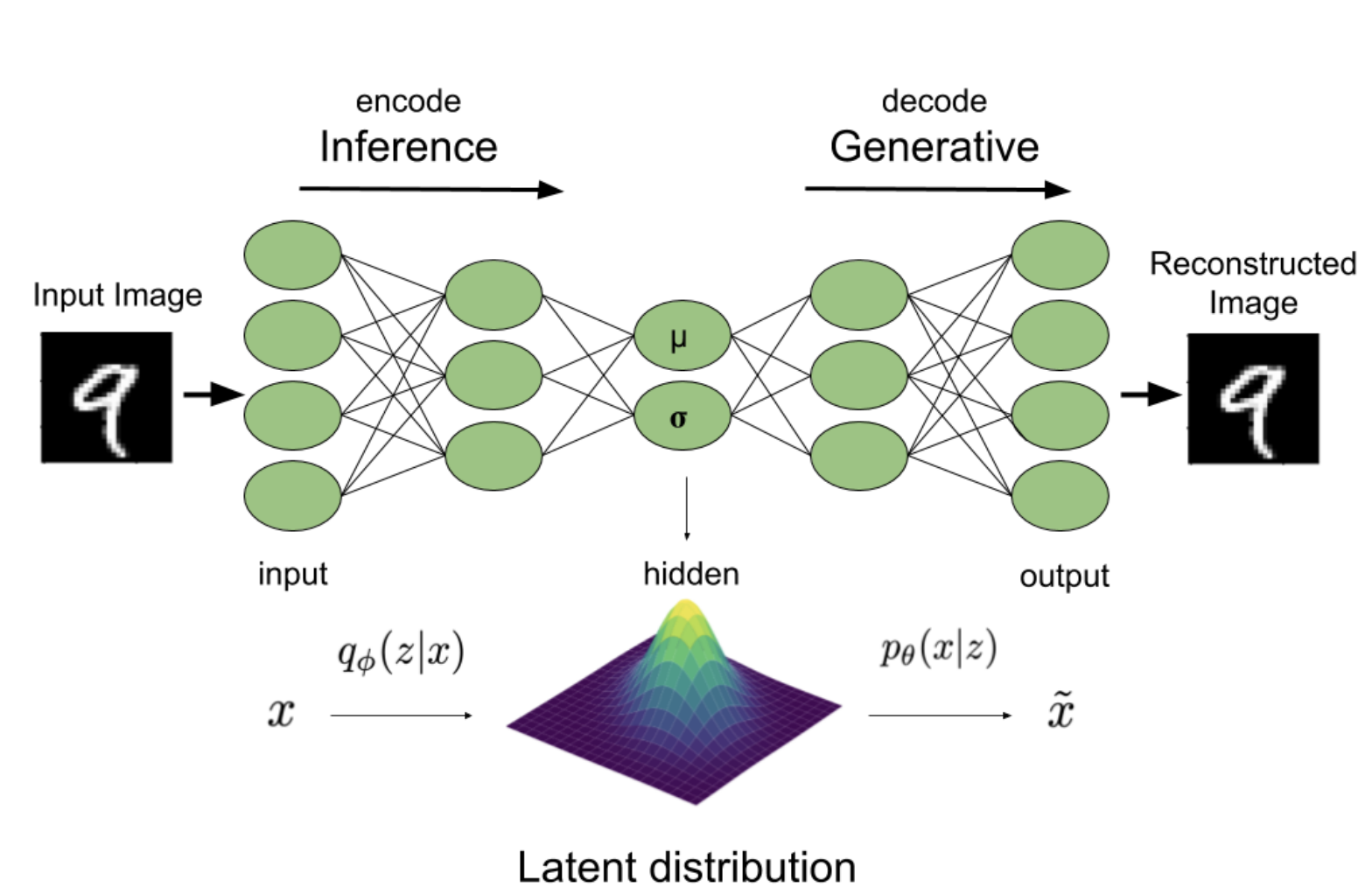
37. Encoder와 Decoder의 구조가 Autoencoder(AE)와 닮았고, $q_\phi$ 라는 variational posterior 가 있기 때문에, Variational AutoEncoder (VAE)가 되는 것이다.

38. 지금까지는 ELBO식을 전개하며 gradient를 구할 수 있게 하고, 그것을 이용하여 ELBO를 최대화 할 수 있다고 했다. 하지만, 이 식이 AE 관점에서 어떤 특성을 가지고 있는지에 대해서 구체적으로 설명하지 않았다. AE 관점에서 ELBO식을 파헤쳐보려고 한다. 일단 ELBO 식을 약간 조작해보면 아래와 같다.

$$ \begin{aligned} \mathcal{L}(\mathbf{x}; \theta, \phi) &= \mathbb{E_{q_\phi(z \mid \mathbf{x})}} \left[ \log p(\mathbf{z}, \mathbf{x}; \theta) - \log q_\phi(z \mid \mathbf{x}) \right] \\ &= \mathbb{E_{q_\phi(z \mid \mathbf{x})}} \left[ \log p(\mathbf{z}, \mathbf{x}; \theta) - \log p(z) + \log p(z) - \log q_\phi(z \mid \mathbf{x}) \right] \\ &= \mathbb{E_{q_\phi(z \mid \mathbf{x})}} \left[ \log p(\mathbf{x} \mid z; \theta) \right] - D_{\mathrm{KL}}\left( q_\phi(z \mid \mathbf{x}) | p(z) \right) \end{aligned} $$

• KL 식은 아래와 같기 때문에 KL로 묶이는 것이다.
  • $D_{\mathrm{KL}}\left( q_\phi(z \mid \mathbf{x}) | p(z) \right) = \sum_{q_\phi(z \mid \mathbf{x})} q_\phi(z \mid \mathbf{x}) \log \frac{q_\phi(z \mid \mathbf{x})}{p(z)} = \mathbb{E_{q_\phi(z \mid \mathbf{x})}} \left[ \log q_\phi(z \mid \mathbf{x}) - \log p(z) \right]$

$$\mathbb{E_{q_\phi(z \mid \mathbf{x})}} \left[ \log p(\mathbf{x} \mid z; \theta) \right]$$

39. 우리는 훈련 시 이 ELBO를 최대화하는 것을 목표로 한다. 일단 세번째 줄의 첫번째 항만 가져와서 봐보자. 이 항을 계산하기 위해서 기대값이기 때문에, Monte Carlo 를 사용할 수 있다. $q_\phi(z|x)$ 에서 샘플을 추출하고 그것을 decoder(p)에 넣어 확률이 나오는 것으로 식을 해석할 수 있다.
    • 앞서 우리는 위에서 $q_\phi(z|x)$ 는 variational posterior를 추론하는 neural network라고 배웠다.
    • 그렇다면 encoder는 이미지(x)를 보고 이미지에 맞는 latent variable z의 분포, 즉 평군과 분산의 값이 나오고 이를 샘플링하여 특정 z의 값을 얻는 것이다.
      • 만약 훈련 시 $q_\phi(z|x)$ 이 가우시안 분포를 띈다면, 인코더를 통해 이미지(x)를 맞춰서 얻은 결과에 따라 정의되는 평균과 분산을 갖는 가우시안 분포가 나올 것이다. 그럼 이 분포로 샘플링을 하여 $\hat{z}$ 를 얻는다.
    • 훈련 시 우린 이 $\hat{z}$를 다시 neural network인 decoder에 넣으면 원래 이미지 x를 얼마나 잘 재구성할 수 있는지에 대한 재구성 분포를 얻고 $\hat{x}$ 를 얻는다.
    • 이 항을 Reconstruction Term으로 불린다. 이 항만으로도 약간의 확률적 AE 기능을 한다.
    • VAE Paper Review 31번째 줄 을 보면 식 전개하는 과정을 참고할 수 있다. 추가로 해당 항이 분포에 따라서 Cross Entropy, L2 Loss가 된다는 것을 알 수 있다.

$$-D_{\mathrm{KL}}\left( q_\phi(z \mid \mathbf{x}) | p(z) \right)$$

40. 세번째 줄의 두번째 항을 보면 encoder에서 나온 $\hat{z}$ 가 $p(z)$ 와 유사해지게 한다. 이는 이미지를 잘 재구성할 뿐 아니라 재구성에서 사용하는 latent variable z의 분포도 우리가 사전에 정의한 분포($p(z)$)와 유사해져야 한다는 것이다.
    • 첫번째 항만으로는 새로운 데이터 포인트에서 생성할 방법이 없다. 첫번째 항만 사용한다면, 그저 일반화가 잘되기를 빌어야한다.
    • 잠재 변수가 특정한 모양, 분포를 갖게 정규화 해주는 역할을 하기 때문에도 Variational AE라고 불리는 이유이다.
    • 이 항을 Regularization Term으로 불린다.
    • VAE Paper Review 31번째 줄 을 보면 식 전개하는 과정을 참고할 수 있다.

$$p(x) = \sum_z p(z)p(x|z)$$

41. 결국 첫번째 항은 p(x|z) 가 잘 훈련되기 위한 항이고, 두번째 항은 p(z)가 잘 훈련되기 위한 항이다. 따라서 훈련이 다 끝나고, 생성을 할 땐 p(z)는 미리 알기때문에 $z \sim p(z)$ 으로 추출하고 그것을 $p_\theta(x|z)$ 에 넣으면 x가 생성이 된다.
    • 결국 encoder는 decoder를 훈련시키기 위한 하나의 수단이고, 생성의 관점에서는 decoder만으로 새로운 x를 만들 수 있게 되는 것이다.

---

Reference

• https://deepgenerativemodels.github.io/
• https://www.youtube.com/watch?v=tRArbBf-AbI&list=PLoROMvodv4rPOWA-omMM6STXaWW4FvJT8&index=3&t=4s
• https://wikidocs.net/228835