[CS236] 4. Maximum Likelihood Learning

GoodYoung included in DL Theory Lecture Deep Generative Models

2025-06-30 1141 words 6 minutes

Contents

개요

이번 포스트에서는 CS236 강의의 4강 내용을 정리한다.

3강에선 데이터셋의 분포를 학습하여 Model Family를 파라미터화 하는 방법을 배웠다.

이번 4강에서는 데이터셋에 대하여 모델 파라미터 $\theta$ 를 찾는 방법을 배우게 된다.

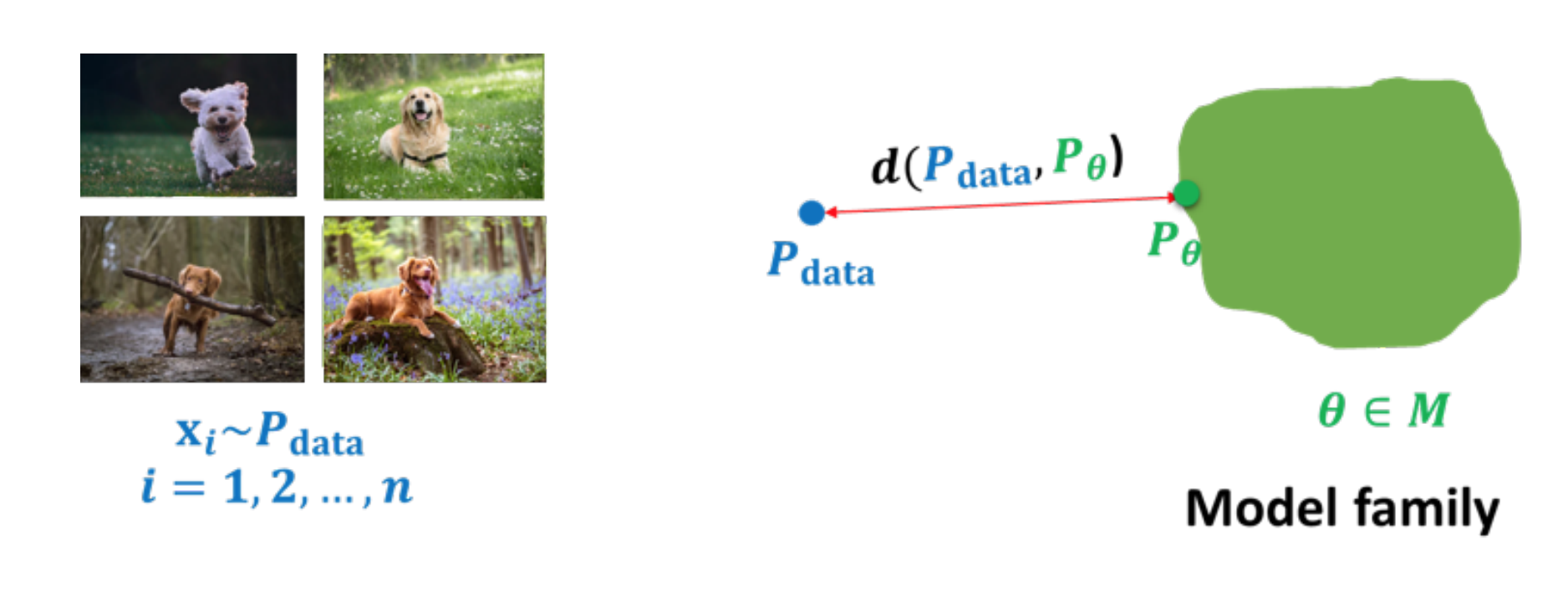
3강에서 다뤘던 내용을 다시 한 번 살펴보자. 데이터가 실제 분포 $P_\text{data}$ 로부터 추출된 m개의 샘플 $\mathcal{D}$ 가 있다고 가정을 해보자.

그럼 생성 모델의 목표는 모델 $\mathcal{M}$ 에서 $P_\text{data}$ 와 가능한 가장 가까운 $P_\theta$ 를 학습하는 것이다.

이때의 모델 $\mathcal{M}$ 은 Bayes net이 될 수 있고, FVSBN이 될 수 있는 것 이다.

하지만 $P_\theta$ 가 완전히 실제 분포를 포착할 순 없다. 왜냐하면 제한된 data의 문제와 컴퓨팅 파워 문제가 있기 때문이다.

784개의 이진 픽셀로 이루어진 이미지를 생각해보면, 가능한 모든 이미지는 $\text{2}^\text{784} \approx \text{10}^\text{236}$ 가지이다. 대략 백만 개의 샘플로는 이 공간을 거의 다룰 수 없다.

그래서 우리는 $P_\text{data}$ 의 분포를 잘 근사하는 $P_\theta$ 를 선택해야한다. 그렇다면 어떤 것이 잘 근사하는 모델($P_\theta$)일까?

잘 근사하는 모델은 우리가 하려는 task에 따라 다르다. (Density Estimation에서는 전체 확률 분포를 잘 근사하는 것이 중요, Specific Prediction Task은 특정 예측을 만드는 분포(조건부 확률)가 중요, Structure or Knowledge Discovery 모델 그 자체의 구조가 중요)

생성의 관점에선 어떤 확률적 추론 쿼리에 답해야 하기 때문에 우린 전체 분포를 배워야한다. 따라서 학습을 Density Estimation 문제로 볼 수 있다.

여기서 말하는 확률적 추론 쿼리(any probabilistic inference query)란 확률 분포로부터 도출되는 질문들(조건부 확률, 마진, 샘플링 등)을 의미한다.

그래서 우리의 목표는 $P_\text{data}$ 에 가장 가까운 $P_\theta$ 를 만드는 것이 제일 중요하다. 그렇다면 가까운 정도를 어떻게 평가할까? 다음 챕터에서 설명 할 것이다.

Kullback-Leibler divergence(KL-divergence)

어떤 두 분포간의 가까운 정도를 측정하기 위하여 Kullback-Leibler divergence(KL-divergence)지표를 사용하게 된다. 수식은 아래와 같다.

$$D_{\text{KL}}(p || q) = \sum_x p(x) \log \frac{p(x)}{q(x)}$$

KL-Divergence는 몇가지 특징이 있다.

$D_{\text{KL}}(p || q) \geq 0$ 이고, 같을 땐 $p = q$ 일 때 이다.
$D_{\text{KL}}(p || q) \not = D_{\text{KL}}(q || p)$ 으로 비대칭적인 성질을 지닌다.
이 지표는 정보이론 관점에서 p와 q에 기반한 압축 방식이 얼마나 잘되는지 보여준다. (p가 진짜 분포이고 q가 학습한 분포)
- q의 분포로 p를 인코딩을 했을 때 생기는 비트 낭비량을 확인할 수 있다.

우리의 목표는 $P_\theta$ 가 $P_\text{data}$ 와 가깝도록 만드는 것이기 때문에 $D_{\text{KL}}(P_\text{data} || P_\theta)$ 로 표현할 수 있다.

따라서 KL-Divergence의 값을 확인하여 data를 잘 압축할 수 있는 모델을 선정해야한다.

KL이 작을수록, 압축 손실도 작아짐 → 더 나은 모델

$$ D_\text{KL}(P_\text{data} || P_\theta) = \mathbb{E_{x \sim P_\text{data}}}[\log P_\text{data}(x)] - \mathbb{E_{x \sim P_\text{data}}}[\log P_\theta(x)] $$

위 KL을 다음과 같이 분해가 가능하고, 앞 항은 $P_\theta$ 에 영향받지 않는 상수이기 때문에 두번째 항에 집중을 할 것이다. 그렇게 되면 수식은 아래와 같아진다.

$$ argmin_\theta \ D_(P_\text{data} || P_\theta) = argmin_\theta -\mathbb{E_{x \sim P_{\text{data}}}} [\log P_\theta(x)] = argmax_\theta \ \mathbb{E_{x \sim P_{\text{data}}}} [\log P_\theta(x)] $$

그럼 이제 KL을 최소화 하기 위하여 두번째 항을 최대화 하는것이 목표이다.

이 수식을 통하여 알 수 있는 KL의 특징이 있다. 바로 두 모델 간 KL을 비교했을 때 누가 가까운지는 알지만 얼마나 가까운지 (정확한 거리)는 모른다는 것이다.

$D_(P_\text{data} || P_{\theta_{1}}) - D_(P_\text{data} || P_{\theta_{2}})$ 가 계산이 되면 상수(첫번째 항)가 사라져서 거리를 모르게 된다.

이제 이 수식을 풀려고 보니, 정리된 수식의 모든 $P_\text{data}$를 우리는 일반적으로 (expected log-likelihood) 구할 수 없다. 왜냐하면 현실에선 이 기대값을 계산할 수 없으므로 주어진 데이터 샘플의 평균으로 근사 해야한다. (empirical log-likelihood) 따라서 데이터 샘플의 평균으로 근사하면 아래와 같은 식이 나오고, 그것을 최대화 하는 $\theta$를 찾는 방향으로 학습을 진행하면 된다.

이 아이디어는 monte carlo 추정에서 나왔다.
샘플 수가 많아질수록 무작위성은 줄어들고 함수의 실제 기대값에 가까워진다. (분산도 작아진다. -> 근사치가 점점 신뢰 가능해진다.)

$$E_D [\log P_\theta(x)] = \frac{1}{|D|} \sum_{x \in D} \log P_\theta(x)$$

$$max_\theta \ \frac{1}{|D|} \sum_{x \in D} \log P_\theta(x)$$

Gradient Descent

지금까지 했던 KL-Divergence와 Monte Carlo의 개념을 Autoregreesive Model에 적용시켜서 학습 데이터 $D$에 대해 $p_\theta(x)$를 근사하게 만들면 다음과 같다.

$$ P_\theta(x) = \prod_{i=1}^n p_{\text{neural}}(x_i \mid x_{<i}; \theta_i) $$

$$ \log \mathcal{L}(\theta, D) = \sum_{j=1}^m \sum_{i=1}^n \log p_{\text{neural}}(x_i^{(j)} \mid x_{<i}^{(j)}; \theta_i) $$

$j$: Datapoint, $i$: Datapoint의 변수

하지만 이것은 closed form이 아니여서 최적화가 필요하다. 최적화를 하는 방식은 경사 하강법(gradient descent)를 이용하는 것이다.

비선형/비볼록이라 closed-form인 경우 경사 하강법을 이용하면 꽤 잘 풀리는 경우가 많다.

다음은 해당 식을 가지고 경사 하강법을 하는 단계이다.

$\theta_0$: 랜덤 초기화
$\nabla_\theta \log \mathcal{L}(\theta, D)$: 기울기 계산
$\theta_{t+1} = \theta_t + \alpha_t \nabla_\theta \log \mathcal{L}(\theta, D)$: 의 식을 가지고 업데이트
t가 T에 수렴할 때 까지 반복. (최적화의 $\theta$로 수렴하게 된다.)

Stochastic Gradient Descent

위와 같이 경사하강법으로 하게 되면 파라미터의 공유가 없다면, 모든 데이터 포인트를 각각 분리해서 최적화 한다. 이게 데이터 포인트의 수가 많아지면 오버헤드가 생길 수 있다.

따라서 Stochastic Gradient Descent가 나오게 되었다. 이 방법은 모든 데이터셋을 최적화에 활용하는 것이 아니라, 데이터셋 $D$를 나눈 배치(미니 배치)에서 하나의 데이터를 가지고 파라미터를 업데이트 하는 방법이다.

이 방법은 확률적 근사를 한 것이고, 위에서 나온 Monte Carlo의 방법과 같다.

$$ \nabla_\theta \ell(\theta) = \sum_{j=1}^m \sum_{i=1}^n \nabla_\theta \log p_{\text{neural}}(x_i^{(j)} \mid x_{<i}^{(j)}; \theta_i) $$

위은 gradient 식을 다시 나타낸 것인데 위 식에서 $D$가 만약에 클 때 Monte Carlo를 사용하여 식을 변형할 것이다. 그렇게 되면 아래의 식과 같이 된다.

$$ \begin{aligned} \nabla_\theta \ell(\theta) &=m\sum_{j=1}^m\frac{1}{m} \sum_{i=1}^n \nabla_\theta \log p_{\text{neural}}(x_i^{(j)} \mid x_{<i}^{(j)}; \theta_i) (by \ \text{Monte Carlo})\\ &= m \cdot \mathbb{E_{x^{(j)} \sim D}} \left[ \sum_{i=1}^n \nabla_\theta \log p_{\text{neural}}(x_i^{(j)} \mid x_{<i}^{(j)}; \theta_i) \right] \end{aligned} $$

위 식을 보면 uniform 분포라는 가정과 함께 데이터셋에서 샘플을 추출할 수 있고, 해당 샘플에 대해서만 기울기를 평가하고 모델 학습에 이 비선형성을 부여할 수 있게 된다.

Drawback

지금까지의 학습 방식들은 쉽게 과적합을 할 수 있는 문제가 있다. 따라서 모델이 unseen data에 대해서 잘 맞추는 generalization이 제일 중요하다.

일반화를 하기 위해 학습에서 정규화를 해야한다.

너무 정규화를 진행하면 모델이 단순해지는 한계인 bias가 일어나고(under-fitting), 정규화를 하지 않으면 모델이 너무 데이터에 fit해지는 한계인 variance(over-fitting)이 일어난다.

이런 것을 막기 위해선 weight sharing, regularization, hold-out (k-fold)등의 방법이 있다.

Summary

긴 흐름을 단순화하여 정리할 필요가 있어보여 이번 챕터를 정리하려고 한다.

이번 챕터에서는 생성 모델의 학습 방법에 대해 다루었다. 생성 모델의 목표는 $P_\text{data}$를 잘 근사하는(가까운) $P_\theta$를 만드는 것이 중요한데 두 분포가 잘 근사하는(가까운) 정도를 측정하기 위하여 KL-Divergence가 도입되었다.

KL-divergence의 수식을 전개해 보면,이를 최소화하는 것은 결국 다음 log-likelihood 기대값을 최대화하는 문제와 같다는 것을 알 수 있다: ($argmax_\theta \ \mathbb{E_{x \sim P_{\text{data}}}} [\log P_\theta(x)]$)

식을 풀려고 봤더니 $P_\text{data}$ 때문에 식을 직접적으로 계산할 수 없다. 이를 해결하기 위해 monte-carlo추정을 사용한다. 이는 모든 $P_\text{data}$를 사용하는 것이 아닌 그 중에 샘플을 추출한 데이터 샘플의 평균을 사용하여 기대값을 근사하는 방법(기대값 -> 평균)이다. 이 방법을 사용하면 MLE(Maximum Likelihood Estimation)의 수식이 나오게 되는 것이다. ($max_\theta \ \frac{1}{|D|} \sum_{x \in D} \log P_\theta(x)$)

이렇게 배운 학습 방식들을 Autoregressive Model 구조에 맞게 적용해보려고 한다. (학습 데이터 D에 대해 $p_\theta(x)$를 $p_\text{data}$에 근사하게 학습할 수 있다.) ($\log \mathcal{L}(\theta, D) = \sum_{j=1}^m \sum_{i=1}^n \log p_{\text{neural}}(x_i^{(j)} \mid x_{<i}^{(j)}; \theta_i)$)

하지만 이때 유도된 식은 계산할 수 없어서, 경사 하강법(gradient descent)을 사용하여 파라미터($\theta$) 최적화를 진행한다.

이 경사 하강법(gradient descent)은 데이터 양이 많아지게 되면 모든 데이터 포인트를 분리해서 계산하여 오버 헤드가 생긴다는 단점을 지니고 있어, 확률적 경사 하강법(stochastic gradient descent)을 사용해 배치마다 하나의 데이터를 사용하여 파라미터 최적화를 진행하는 방법도 있다.

난 여기까지 정리하면서 의문이 들었다. 왜 Autoregressive Model에서만 최적해를 못구해서 경사 하강법이 나온 것인가?

내가 남긴 의문에 찾은 답을 하자면 다음과 같다.
동전 예제, 이항 분포처럼 단순한 경우엔 Monte Carlo 근사만 해도 최적화가 가능(직접 미분해서 최대화의 지점을 찾을 수 있음)
Autoregressive Model 처럼 구조가 복잡한 경우엔 경사 하강법으로 해결해야 한다. (미분은 가능하지만, 해석적으로 $\theta$를 찾을 수 없기 때문)