GoodYoung Dev Blog
Posts Tags Categories
GoodYoung Dev Blog

Contents

[CS236] 3. Autoregressive Models

GoodYoung included in DL Theory Lecture Deep Generative Models
   1012 words   5 minutes 

개요

  1. CS236: Deep Generative Models (Stanford)는 스탠포드 대학교에서 진행하는 딥러닝 기반 생성 모델(Deep Generative Models) 에 대한 심화 강의이다.

  1. 이번 포스트에서는 CS236 강의의 3강 내용을 정리한다.

  1. 3강에서는 주어진 데이터셋 D의 분포를 학습하여, 이로부터 새로운 샘플을 생성하는 방법을 배운다.
  • 그렇게 하기 위해서 2가지 절차가 진행되어야 한다:
    • Model Family를 파라미터화 (3강에서 다룰 내용)
    • 데이터셋 D에 대하여 모델 파라미터 $\theta$ 를 찾는 방법 (4강에서 다룰 내용)

Autoregressive Models

$$ \begin{aligned} p(x_1, x_2, \ldots, x_{784}) &= p(x_1),p(x_2 \mid x_1),p(x_3 \mid x_1, x_2), \cdots, p(x_{784} \mid x_1, \ldots, x_{783}) \\ p(x_1, \cdots, x_{784}) &= p_{\text{CPT}}(x_1; \alpha_1) \cdot p_{\text{logit}}(x_2 \mid x_1; \alpha_2) \cdot p_{\text{logit}}(x_3 \mid x_1, x_2; \alpha_3) \cdots p_{\text{logit}}(x_n \mid x_1, \cdots, x_{n-1}; \alpha_n) \\ \end{aligned} $$

  1. Autoregressive Model은 각 픽셀을 이전 픽셀들에 대한 조건부 확률로 예측하는 모델이다.

  1. 이러한 조건부 확률을 계산을 하기 위해서 Chain rule factorization을 사용한다. 하지만 이때 모든 확률 조건들을 저장할 수 없다. 따라서 어떤 신경모델, 함수를 사용하여 조건문을 모델링 하려고 한다. 위의 두번째 수식 처럼 logistic regression 함수를 이용한 방법이 그 예시이다.

$$ \begin{aligned} p_{\text{CPT}}(X_1 = 1; \alpha_1) = \alpha_1 &, p(X_1 = 0) = 1 - \alpha_1, \\ p_{\text{logit}}(X_2 = 1 \mid x_1; \alpha_2) &= \sigma(\alpha_2^0 + \alpha_2^1 x_1), \\ p_{\text{logit}}(X_3 = 1 \mid x_1, x_2; \alpha_3) &= \sigma(\alpha_3^0 + \alpha_3^1 x_1 + \alpha_3^2 x_2) \end{aligned} $$

  1. MNIST 데이터셋으로 Autoregressive Model을 구성하는 수식을 살펴보게 되면 위의 수식과 같다. 첫번째 픽셀이 black or white인지 조건부 확률 테이블(CPT)에서 값을 받아 배정된다.(보통 black) 그 후 순서에 따라 각 값을 예측하게 된다.

Fully Visible Sigmoid Belief Network (FVSBN)

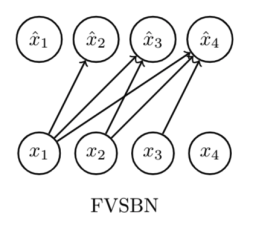
  1. 초창기 autoregressive model인 FVSBN은 chain rule을 이용해 확률분포를 나타낸 이후, 많은 컴퓨팅 파워를 요구하는 조건부 확률을 매개변수화한 이후 logistic regression 알고리즘을 적용해 학습하는 생성모델 알고리즘이다.

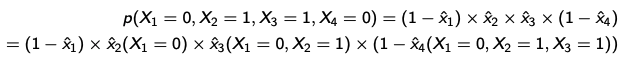
  1. 만약 pixel이 4개라고 가정을 하면, 이전 픽셀에 따라서 값이 다른 것을 확인할 수 있다.

  1. 이 모델의 경우 파라미터는 $1+2+3+\cdot\cdot\cdot+n \approx n^2/2$ 인 것도 확인할 수 있다.

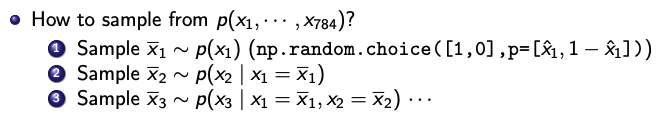
  1. FVSBN에서 sampling하는 방법이다. 랜덤한 난수를 먼저 생성하고, 그 난수($\bar{x_1}$)로부터 $\bar{x_2}$ 가 나오게 된다.
  • 하지만 FVSBN의 sampling 결과가 좋진 않다.

Neural Autoregressive Density Estimation (NADE)

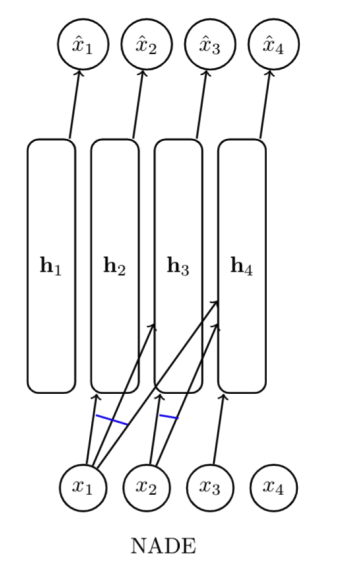
  1. NADE는 많은 컴퓨팅 파워를 요구하는 FVSBN의 한계를 보완하기 위해서 logistic regression 대신 Neural Network를 사용한 모델이다.

$$ \begin{aligned} h_i &= \sigma(W_{\cdot,<i} x_{<i} + c) \\ \hat{x_i} = p(x_i \mid x_1, \ldots, x_{i-1}) &= \sigma(\alpha^\top h_i + b_i) \end{aligned} $$

  1. 위 수식의 $h_i$는 neural network를 의미한다. NADE는 Weight Sharing(Weight tying)기법을 활용하여 계산량을 대폭 줄였다.

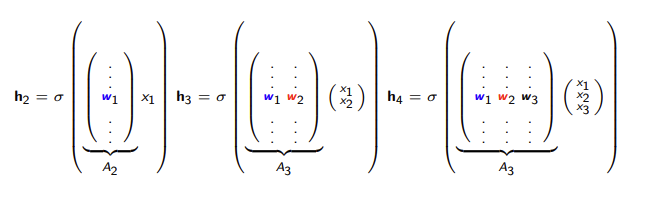
  1. Weight Sharing은 학습 과정에서 은닉층($h_i$)에서 사용하는 가중치 $w_i$를 동일하게 유지하는 방법이다.
  • 층이 깊어질수록 기존 가중치 벡터 (W)에 열벡터 하나만 추가하는 것으로 생각하면 된다.

  1. 이런 결과로 계산 복잡도가 O(n)으로 줄어든 것을 확인할 수 있다.

  1. 위 사진이 NADE의 생성 결과인데, 왼쪽이 sample이고 오른쪽이 생성 결과이다. 이미지 구조(분포)를 꽤나 잘 파악하고 있는 것으로 확인할 수 있다.

  1. 생성의 작동 방식은 왼쪽 sample에서 픽셀 값을 가져오고 NADE가 계산을 통하여 확률 값이 나오게 된다. 따라서 각 픽셀에 대한 확률 값이기 때문에 오른쪽 샘플의 결과는 0~1사이의 확률값이기때문에 이미지가 부드러워 보인다.

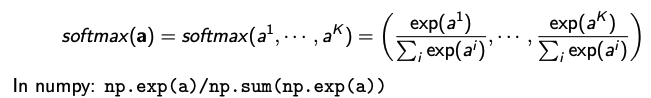
  1. 지금까지는 이진 데이터만 다루었다. 하지만 color 이미지와 같은 범주형 변수일 때는 어떻게 작동 할까? $x_i \in {0, \ldots, K}$ 인 다항 변수의 모델링이 필요할 것이다.

  1. 다항 변수의 모델링을 하기 위해서 각 $x_i$에 softmax를 취하여 범주형 확률 분포를 만들어주면 기존의 조건부 확률을 계산할 수 있게 된다.

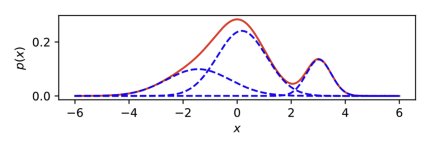
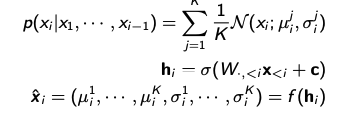
  1. 그렇다면 연속형 변수일 때는 어떻게 작동 하는지 알아 볼 것이다. $x_i \in \mathbb{R}$ 를 모델링 하기 위하여 Gaussian Mixture를 사용한다.

  1. 따라서 각 $x_i$에 대하여 K개의 평균, 분산을 예측하여 연속 확률 분포를 얻을 수 있게 된다.
  • 이 평균, 분산을 얻을 땐 신경망을 사용하게 된다.

Autoregressive Autoencoders

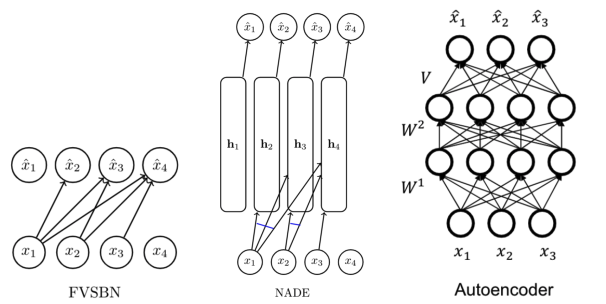
  1. Autoregressive Model은 Autoencoder와 유사하게 보일 수 있다.

  1. 하지만 Autoencoder는 데이터의 분포를 정의하는 생성 모델이 아니기 때문에 Autoregressive model과 차이가 있다.

  1. Autoregressive model은 시점 $i$ 이전 데이터만을 가지고 데이터 $x_i$를 추정하지만, 기존의 autoencoder는 전체 데이터의 특징을 학습을 한다. 이러한 Autoencoder를 생성 모델로 만들기 위한 방법이 있다. 바로 데이터에 대한 입력 순서를 강제로 정의하여 각 출력이 이전 값에만 의존하게 만드는 방법이다.

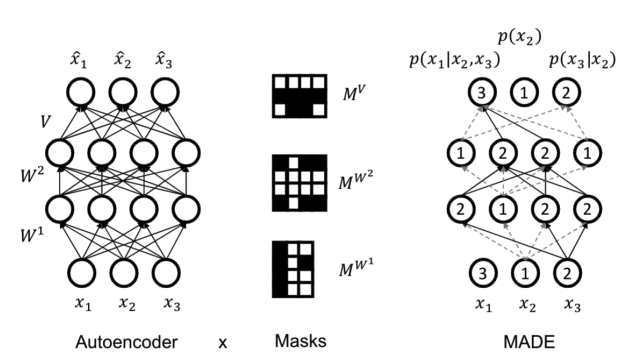
  1. Autoencoder에서 입력 순서를 강제로 정의하는 방법은 일부 weight을 0으로 설정하는 Masking 방법이 있다. Masked Autoencoder for Distribution Estimation (MADE)은 이러한 방식을 통해 오토인코더 구조를 가지고 확률 분포를 예측하는 autoregressive model이다.

  1. 각 출력 유닛이 자신보다 앞선 입력에만 연결되도록 설정한다. 그렇게 되면 단일 네트워크(single pass)로 조건부 확률을 계산하면서 생성 모델의 역할을 수행할 수 있다.
  • 다음은 MADE의 자세한 작동 방식이다:
    1. 각 은닉 노드에 정수 마스크 값 (1부터 n-1까지)을 랜덤한 숫자를 배정한다.
    2. 부모 노드의 숫자가 자식 노드의 숫자보다 작거나 같으면 ($<= i$) 연결을 유지한다.
    3. 부모 노드의 숫자가 자식 노드의 숫자보다 크면 ($> i$) 연결을 제거한다.

  1. 이 방식으로 전체 네트워크는 DAG(Directed Acyclic Graph) 구조를 가지게 되어 autoregressive 구조가 성립된다.

Recurrent Neural Nets (RNN)

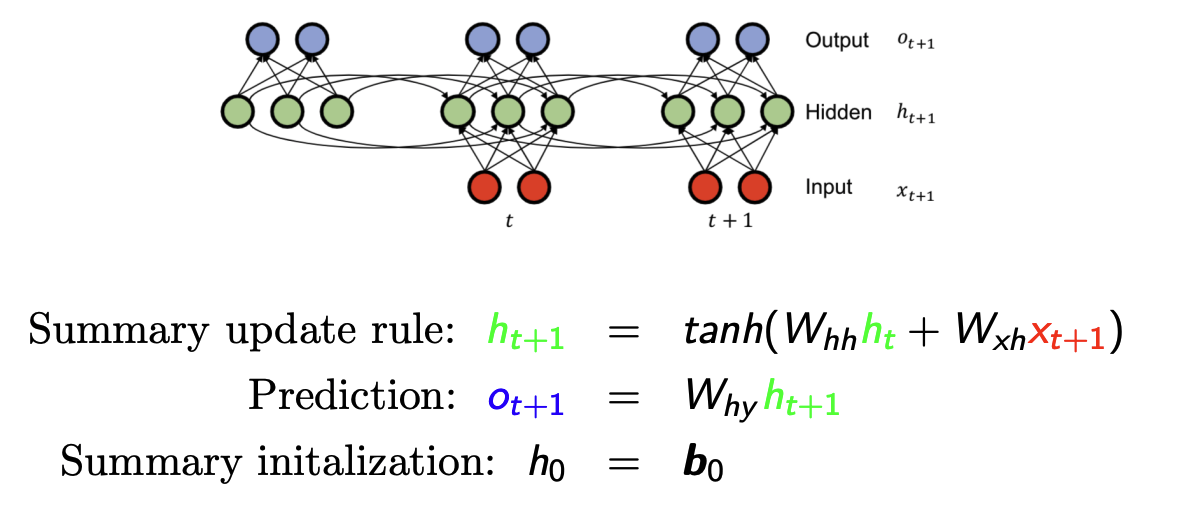
  1. 지금까지의 autoregressive model은 시점 $i$ 이전의 데이터를 다 가지고 있으면서 예측에 활용 했어야 했다. 이렇게 되면 history가 길어질 수록 수식이 길어지는 단점이 있다. 이런 문제를 해결하고자 시간 순서에 따라 정보를 압축하여 유지하고 반복하여 업데이트 하는 RNN 구조가 나오게 되었다.

  1. $h_\text{t+1}$ 에서 이전 입력들을 요약 및 업데이트하고, 이것($h_\text{t+1}$)을 가지고 출력 $o_\text{t+1}$ 을 예측한다. 또 예측한 $o_\text{t+1}$ 를 다음 입력으로 사용한다.

    • rnn의 행렬 계산을 이해하기 쉽게 정리 한 것이다.
    • 출처

  1. 이런 rnn을 사용하면 입력 길이가 고정되지 않아도 된다. 또한 컴퓨팅의 비용이 상당히 줄어드는 장점이 있다. 하지만 long-term dependency의 문제가 있고, 여전히 입력 순서는 필요하다는 단점이 있다. 또한 훈련, 생성시 속도가 느리다는 단점이 있다.
  • 이러한 단점을 해결하기위하여 attention based 모델이 등장했다.

PixelRNN

  1. Autoregressive의 방법은 이미지 분야에도 적용이 되었다. 바로 PixelRNN이다. $p(x_t \mid x_{1:t-1})$ 를 예측하기 위하여 아래 수식과 같이 R,G,B의 세개의 값을 예측을 해야한다.

$$ p(x_t \mid x_{1:t-1}) = p(x_t^{\text{red}} \mid x_{1:t-1}) \cdot p(x_t^{\text{green}} \mid x_{1:t-1}, x_t^{\text{red}}) \cdot p(x_t^{\text{blue}} \mid x_{1:t-1}, x_t^{\text{red}}, x_t^{\text{green}}) $$

  • 해당 모델 결과를 보면, 모델이 이미지의 구조를 어느정도 파악하고 있음을 알 수 있다.

PixelCNN

  1. CNN구조에 autoregresive를 적용시킨 모델도 있다. 바로 PixelCNN이다. 이 모델은 CNN 구조를 사용하면서 이웃 픽셀들의 정보를 가지고 다음 pixel을 예측하는 방법이다.

  1. 하지만 autoregressive하기 위하여 MADE방법 처럼 masked convolution을 사용하여 예측에 시도하는 방법이다.

Summary

  1. 생성 모델은 주어진 데이터셋 $D$로부터 데이터가 생성되는 확률 분포 $p_\text{data}$를 추정하여, 이 분포로부터 가능한 데이터 샘플 $x \sim p_\text{data}(x)$을 생성하는 방식이다

  1. 그러나 실제로 $p_\text{data}$를 직접 구하는 것은 불가능하므로, 모델은 이와 유사한 분포를 나타내는 파라미터 $\theta$를 학습하여 근사 분포 $p_\theta(x)$ 를 모델링하는 방식(여기서 여러 생성 알고리즘이 등장)으로 작동한다.
  • 이때 $p_\theta(x)$ 로부터 생성한 데이터 $\hat{x}$ 가 실제 데이터의 분포에서 생성한 데이터 x와 유사하게 설정할 수 있게 되는 것이다.

  1. Autoregressive model은 $p_\theta(x)$ 를 연쇄 법칙을 통해 $i$ 시점 데이터 $x_i$ 의 가능도(확률) $p(x_i)$ 는 이전 시점까지의($i-1$) 데이터를 바탕으로 예측하는 조건부 확률 형태를 나타낸다.

  1. 이런 Autoregressive model이 샘플링하고, 확률을 계산하는 방법은 아래와 같다.

Reference

Updated on 2025-05-07
 Bayesian network, Conditional Independence, CS236
Back | Home