[Paper Review]Auto-Encoding Variational Bayes(VAE)

GoodYoung included in Paper Review DL

2024-08-26 1345 words 7 minutes

Contents

개요

Generative분야에서 기초가 되는 논문인 VAE에 관한 리뷰를 할 것이다.

Introduction

연속적인 latent variable(잠재변수)나 파라미터가 계산이 힘든 후방 확률 분포를 가지는 확률 모델을 어떻게 효과적으로 추론하고 훈련을 시키는 방법에 대해 설명이 나온다.

디코더만으로 학습 및 훈련을 진행할 수 없어서 인코더를 가져온 것이다.
해당 내용은 Method 부분에서 자세하게 다룰 것이다.

기존의 방법인 Variational Bayesian(VB) 방법은 계산하기 힘든 사후 확률을 적절하게 최적화 한다.

하지만 이 방법은 후방 확률에 대한 기대값의 분석적 해결책을 요구하며, 일반적인 경우에도 계산이 어렵다.

그래서 본 논문에서 기존 변동의 lower bound의 reparameterization가 어떻게 간단하고 다른 비편향적인 estimator의 lower bound를 만드는지 알려준다.

Stochastic Gradient Variational Bayes(SGVB) estimator가 posterior inference(후방 추론)을 잘 하도록 한다.

이는 확률적 경사 하강법을 사용하여 곧바로 최적화도 된다.

독립적이고 동일한 분포를 띄는 이 latent variable에서 본 논문은 Auto-Encoding VB 알고리즘을 제안한다.

SGVB estimator를 사용하여 추론과 learning을 neural network인 recognition model에 효율적으로 적용한다.

비싼 추론 없이 모델 param을 효과적으로 배우는 방법을 사용한다.
해당 estimator를 사용하면 효과적인 후방 추론을 수행하게 하여 최적화가 된다.

위처럼 neural network에서 recognition으로 사용하게 되면 variational auto-encoder(VAE)가 된다.

Method

어떠한 dataset이 있을 때 실제 파라미터 $\theta$와 latent variable $z^\text{(i)}$ 는 우리가 알 수 없다.

따라서 본 논문에선 Intractability하고 large dataset에도 잘 최적화 할 수 있는 알고리즘을 개발을 한다.

그렇게 하기 위하여 세가지 문제를 설명한다.

파라미터 $\theta$ 에 대한 효율적인 근사를 하는 문제
관찰된 값 $x$와 $\theta$를 기반으로 latent variable $z$를 효율적인 사후 추론 하는 문제
$x$의 효율적인 근사 추론하는 문제
- 이미지 노이즈 제거(denoising), 이미지 복원, 초해상도 등 가능

이런 문제를 해결하기 위하여 recognition model ($q_{\phi}(z \mid x)$)을 도입하였다.

이는 $p_{\theta}(x \mid z)$를 가장 근사화 하는 네트워크 이다.

이 네트워크의 목표는 decoder에서 training data(x)의 likelihood를 최대화 하고 싶은 것이다.

따라서 해당 목표를 수학 식으로 표현하자면 아래와 같다. 이는 x가 나올 수 있는 확률 ($p_{\theta}(x)$)이 가장 커지는 distribution을 찾는 것으로 생각하면 된다.

$$p_{\theta}(x) = \int p_{\theta}(z) , p_{\theta}(x \mid z) \ dz $$

이때 위 식은 아래의 식에서 나왔다.

$$\frac{P(x, z)}{P_{\theta}(z)} = p(x \mid z)$$

따라서 식을 정리하면 아래와 같다.

$$p_{\theta}(x) = \int P(x, z) \ dz $$

위 식을 해석하면 x와 z가 동시에 일어날 확률을 모든 z에 대해서 적분하면 그것이 x의 확률이 되는 것이다.

하지만 문제는 모든 z에 대해서 적분을 하기가 intractability하는 것이다.

이 문제를 해결하기 위하여 확률적 인코더인 $q_{\phi}(z \mid x)$ (encoder)가 나오게 되었다.

$q_{\phi}(z \mid x) \approx p_{\theta}(z \mid x)$ 로 근사한 것이다.

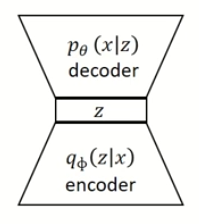
Evidence LowerBOund (ELBO)

다음은 data likelihood를 어떻게 최적화 하는지에 대해서 설명을 할 것이다. 먼저 우리의 목적인 $p_{\theta}(x^i)$의 식을 풀어보자면 아래와 같다.

$$\log p_{\theta}(x^{(i)}) = E_{z \sim q_{\phi}(z \mid x^{(i)})} \left[ \log p_{\theta}(x^{(i)}) \right]$$

적분에서 기대값으로 변경하기 위하여 log를 씌우고 Decoder에서 $z$가 $q_{\phi}(z \mid x^{(i)})$ (encoder)의 분포를 따를 때를 의미한다.

위 식을 조금 더 분해하면 아래와 같다. 베이즈 정리를 사용하여 식을 변형하고 상수를 곱하였다. $$= E_{z} \left[ \log \frac{p_{\theta}(x^{(i)} \mid z) p_{\theta}(z)}{p_{\theta}(z \mid x^{(i)})} \right] (\therefore p(z \mid x^{(i)}) = \frac{p(x^{(i)} \mid z) p(z)}{p(x^{(i)})})$$

$$= E_{z} \left[ \log \frac{p_{\theta}(x^{(i)} \mid z) p_{\theta}(z)}{p_{\theta}(z \mid x^{(i)})} \frac{q_{\phi}(z \mid x^{(i)})}{q_{\phi}(z \mid x^{(i)})} \right] $$

위 식에서 log 변환을 하여 아래와 같은 식을 만들게 된다.

$$ = E_{z} \left[ \log p_{\theta}(x^{(i)} \mid z) \right] - E_{z} \left[ \log \frac{q_{\phi}(z \mid x^{(i)})}{p_{\theta}(z)} \right] + E_{z} \left[ \log \frac{q_{\phi}(z \mid x^{(i)})}{p_{\theta}(z \mid x^{(i)})} \right] $$

다음의 형태를 KL-divergence의 형태로 변경을 하게 되면 최종적인 아래의 식이 나오게 된다. $$= E_{z} \left[ \log p_{\theta}(x^{(i)} \mid z) \right] - D_{KL} \left( q_{\phi}(z \mid x^{(i)}) \parallel p_{\theta}(z) \right) + D_{KL} \left( q_{\phi}(z \mid x^{(i)}) \parallel p_{\theta}(z \mid x^{(i)}) \right) $$

위 식에서 가장 오른쪽 부분을 보면 $p_{\theta}(z \mid x^{(i)})$ 이 부분을 계산을 할 수 없다는 것을 알게 된다. 따라서 저 항은 KL-divergence식이므로 항상 0보다 크다라는 사실로 남겨두게 된다.

계산을 할 수 없는 이유는 decoder에서 $x$를 통해 $z$의 확률 분포를 직접적으로 구할 수 없기 때문이다.
KL-divergence란 두 확률분포가 얼마나 차이가 나는지를 나타내는 지표로 활용이 된다.

따라서 Likelihood를 최대화 하는 것이 목표이므로 맨 오른쪽 식을 제외한 아래의 식을 최대화 하면 된다.

Evidence에 해당되는 x에 대한 확률(marginal likelihood) 을 구하는 것이기 때문에 ELBO라고 불리운다.
또한 최소한 아래의 식 부분을 maximize를 하면 되므로 lowerbound(최저값)라고 불리운다 $$E_{z} \left[ \log p_{\theta}(x^{(i)} \mid z) \right] - D_{KL} \left( q_{\phi}(z \mid x^{(i)}) \parallel p_{\theta}(z) \right)$$

따라서 최적화 단계에서 우린 minimize를 하므로 아래의 식처럼 -를 붙인다. $$\arg \min_{\theta, \phi} \sum_{i} \left( -E_{q_{\phi}(z \mid x_{i})} \left[ \log(p(x_{i} \mid g_{\theta}(z))) \right] + KL(q_{\phi}(z \mid x_{i}) \parallel p(z)) \right)$$

여기서 $E$ 부분을 reconstruction error, $KL$ 부분을 regularization error라고 칭한다.

각 부분을 설명을 하자면 Reconstruction Error는 sampling된 $z$일 때 $x$가 나올 확률을 극대화 해주어 likelihood를 최대화 해주는 loss라고 생각하면 된다.

나중에 L2 loss로 변환이 된다.

또한 Regularization Error는 Encoder를 지난 z의 distribution이 $p(z)$를 알 때 (혹은 가정할 때)랑 일치하게 만든다.

$q_{\phi}$의 분포를 $p(z) \sim \mathcal{N}(0,1)$ 의 분포를 따르게 제한한다.
latent space에 정규 분포 모양을 부여한다.
$q$에서 또한 x의 원래 데이터 분포 p에서 나오게 되도록 하는 항이다.

Optimization: Regularization Error

해당 식을 계산을 하려면 assumption이 필요하게 된다. Encoder를 통과해서 나오는 $z$의 분포는 convariance가 diagonal한 multivariate 정규분포를 따른다.

이는 다변량 정규 분포 중에서도 공분산 행렬이 대각선 형태인 분포를 의미하게 된다.
- 주대각선 요소만을 가진다.

따라서 이를 단순화 하게 하면 해당 분포를 따르면서 평균이 0이고 표준편차가 1인 단위 행렬로 표현이 되는 $P$로 가정을 하게 된다.

결론적으로 위 가정을 토대로 regularization 식을 계산하게 되면 아래와 같다. 계산하기 먼저 다변량 KL-divergence의 식이 아래에 나와 있다.

$$D_{KL}(\mathcal{N}_0 \parallel \mathcal{N}_1) = \frac{1}{2} \left( \text{tr}(\Sigma_1^{-1} \Sigma_0) + (\mu_1 - \mu_0)^{\top} \Sigma_1^{-1} (\mu_1 - \mu_0) - k + \ln \left( \frac{\det \Sigma_1}{\det \Sigma_0} \right) \right)$$

위 식에서 $N1$을 평균이 0, 표준편차가 1인 정규분포 식으로 계산을 하게 되면 최종적인 결과가 나오게 된다. $$KL(q_{\phi}(z \mid x_i) \parallel p(z)) = \frac{1}{2} \sum_{j=1}^{J} \left( \mu_{i,j}^2 + \sigma_{i,j}^2 - \ln(\sigma_{i,j}^2) - 1 \right)$$

따라서 Encoder에서 나온 평균과 분산을 가지고 계산을 할 수 있게 되었다.

Optimization: Reconstruction Error

$$E_{q_{\phi}(z \mid x_i)} \left[ \log(p_{\theta}(x_i \mid z)) \right] = \int \log(p_{\theta}(x_i \mid z)) q_{\phi}(z \mid x_i) , dz$$

Expectation의 계산은 위와 같이 적분 식으로 변형할 수 있게 된다.

이번엔 Reconstruction Error를 계산하는 방법에 대해서 소개를 한다. 네트워크에서 모든 $z$에 대해서 적분하기엔 무리가 있어서 monte-carlo의 방법을 가져오게 된다.

Monte carlo: 무한개의 샘플링을 통한 평균

하지만 이 방법도 시간이 너무 오래걸리는 문제로 무한개가 아닌 $L=1$로 설정하여 이를 대표값으로 쓰게 된다.

랜덤하게 하나만 샘플링하여 그 값을 사용하는 방법으로 생각하면 된다.

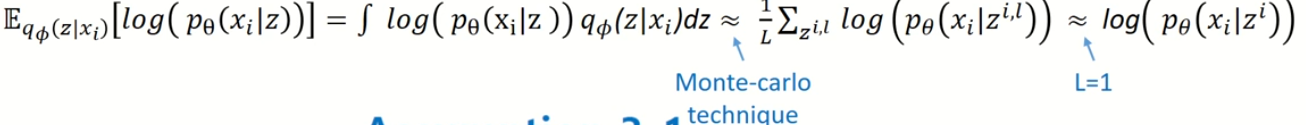
이 역시 확률 분포이므로 확률 분포를 계산하기 위하여 가정을 해야했다. 본 논문에서는 베르누이 분포로 가정을 하였다.

베르누이 이므로 독립 시행이라서 각 차원별로 계산을 해야 한다.
또한 위 그림(식 2번째 줄)에 나온 식을 보면 독립 시행이라 모든 차원을 곱하고 log가 있어서 곱셈이 합으로 표현이 되는 것을 확인할 수 있다.

그렇게 식을 정리하게 되면 cross-entropy 식이 나오게 된다.

참고로 베르누이 분포가 아닌 가우시안 분포를 따른다고 가정을 하면 Mean Squared error 식이 나오게 된다.

Reparameterization Trick

이 trick은 위 그림의 왼쪽 처럼 기존의 encoder model로 평균과 분산을 계산하여 그것을 sampling을 하여 그 분포가 decoder로 간다면 neural network에서 backpropagation이 안된다.

확률적 결과는 미분이 불가능 하기 때문이다.

따라서 미분 가능한 식으로 표현이 가능하게 $N(0,1)$인 표준 정규 분포에서 샘플링을 한 $\epsilon$을 기존 분포의 표준편차에 곱하여 새로운 샘플링 값을 얻으면 z에 대한 식이 나오게 되어 미분이 가능한 식이 되고 따라서 역전파가 가능해진다.

이렇게 하면 기존에 확률적 결과에서 결정적 연산이 된다. 따라서 위 trick을 사용하면 미분이 가능해지면서 동시에 기존과 같은 분포에서 sampling한 결과를 얻게 된다.
기존과 같은 분포를 유지하는 이유?
- 그 이유는 선형 변환(linear transformation)의 성질 때문이다. 가정을 통해 설명을 할 것이다.
- 확률 분포를 정규 분포에서 샘플링을 하고 있다고 가정을 해보자. 이땐 $z \sim \mathcal{N}(\mu, \sigma)$을 따른다.
- 여기서 Reparameterization Trick 을 사용하면 $z = \mu + \sigma \cdot \epsilon, \quad \epsilon \sim \mathcal{N}(0,1)$ 이 된다.
  - 동일한 분포에서 $\epsilon$을 샘플링 해야한다. 따라서 $ \epsilon \sim \mathcal{N}(0,1)$ 을 따른다.
- 이제, $z$의 기대값과 분산을 계산해 보면:
  - 기대값 계산 $$ \begin{aligned} \mathbb{E}[z] &= \mathbb{E}[\mu + \sigma \epsilon] \\ &= \mu + \sigma \mathbb{E}[\epsilon] = \mu + \sigma \cdot 0 = \mu \end{aligned} $$
  - 분산 계산 $$ \begin{aligned} \text{Var}(z) &= \text{Var}(\mu + \sigma \epsilon) \\ &= \text{Var}(\sigma \epsilon) \quad &(\therefore \text{Var}(X+c)=\text{Var}(X)) \\ &= \sigma^2 \text{Var}(\epsilon) = \sigma^2 \cdot 1 = \sigma^2 \end{aligned} $$
- 따라서, 결과적으로 ( z )의 분포는 여전히 $z \sim \mathcal{N}(\mu, \sigma^2)$ 가 된다.
- 결론적으로, 정규 분포는 선형 변환(affine transformation)에 대해 불변이다.
  - 즉, 정규 분포에 스칼라를 곱하고 값을 더하는 것은 원래 정규 분포의 성질을 그대로 유지한다.

Overall Arcitecture

따라서 위의 내용들을 종합적으로 나타내면 VAE의 전체적인 구조를 볼 수 있게 된다.

이 구조에서 encoder, decoder를 어떤 분포를 띄게 할 건지에 따라서 구조가 살짝씩 변형이 될 수 있다.

Decoder에서 가우시안 분포를 따른다고 하면 reconstruction error를 MSE로 계산을 하면 된다.