[Paper Review]High-Resolution Image Synthesis with Latent Diffusion Models(LDM)

GoodYoung included in Paper Review DL Diffusion

2025-02-17 1468 words 7 minutes

Contents

개요

DDPM 이후, 고해상도 이미지 생성을 위해 효율적인 latent space에서 확산 과정을 수행하는 LDM에 대해 논문 리뷰를 할 것이다.

Introduction

이미지 합성(Image synthesis)은 최근 가장 빠르게 발전이 되어왔지만, 많은 컴퓨터 계산 비용이 크다.

특히 고해상도 복원 문제는 AR(Autoregressive) 기반 모델들이 자주 사용하지만 모델 수십억 개의 파라미터를 요구한다.

GAN은 학습 방식의 한계 때문에 multi-modal 분포에서는 모델링 하는데 한계가 있다.

이러한 가운데, Diffusion model이 이미지 합성의 여러 분야에서 뛰어난 성과(SOTA)를 보여줬다.

Diffusion 모델은 다른 모델들과 다르게 모델 붕괴(model collapse), 학습 불안정성, 많은 파라미터에서 강점을 지닌다.

이러한 Diffusion 모델도 문제점이 있는데, Diffusion 모델은 mode-covering 성질을 갖고 있다. 그래서 데이터의 모든 세부 패턴을 학습하려는 경향이 있어서 많은 연산 자원을 필요로 하게 된다.

Reweighted Variational Objective 방법이 연산을 줄이려고 하지만 여전히 계산량이 많다.
A100 기준으로 50,000개의 샘플을 생성하는데 5일이 걸린다.

이러한 문제는 두 가지 영향을 보여준다. 첫 번째로는 훈련 시 거대한 컴퓨팅 자원을 필요로 하므로 일반 연구자나 소규모 연구팀에게 접근성이 낮다.

두 번째로는 추론 시 높은 비용과 시간을 소모하여 학습 뿐 아니라 샘플링 시에도 매우 비효율적이다.'

따라서 이 두 가지의 문제를 해결하기 위한 것이 핵심이다.

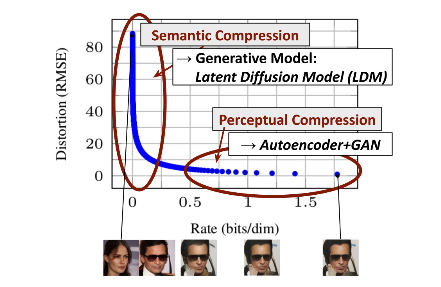
본 논문은 pixel space에서 이미 학습된 diffusion 모델을 분석하는 것 부터 시작한다.

기존의 DM은 픽셀 단위에서 학습을 진행 하였다.
이미지 자체에 대해서 훈련하는 방식이였다.

위 그림과 같이 모든 likelihood-based 모델들의 학습 과정은 두 단계로 나뉠 수 있다.

첫 번째로 높은 주파수 영역의 세부사항을 제거하며 압축을 수행하는 지각적 압축 단계이고, 두 번째로는 실제 생성 모델이 데이터의 의미적이고 개념적인 구성을 학습하는 단계이다.

본 논문은 위 두 단계와 동일하지만, 계산적으로는 더욱 효율적인 공간을 사용하는 모델을 제안한다.

본 논문에서 모델은 두 단계를 제안한다. 첫 번째로 autoencoder를 학습하여 pixel space와 지각적으로 동일하지만, 더욱 효율적인 저차원의 잠재 공간을 만든다.

두 번째로는 추가적인 공간 압축에 의존할 필요 없이 잠재 공간에서 diffusion 모델을 학습시켜 공간적 차원성(spatial dimensionality)에 대해 더 나은 확장성을 갖고 있다.

이미지 자체에 노이즈를 추가하여 학습을 했던 방식과 달리, 잠재 공간에서 학습을 하자는 것이다.

이러한 복잡성 감소 때문에 단 한 번의 네트워크 실행으로도 효율적인 이미지 생성을 할 수 있고, 본 논문은 이 모델을 Latent Diffsion Models(LDMs) 라고 부른다.

이 방법의 장점은 방대한 autoencoder를 한 번만 학습을 하게 된다면, 이를 통해 나온 latent space를 여러 DM 모델의 훈련에 사용할 수 있게 된다.

이는 곧 여러 task에서도 재사용할 수 있게 된다는 것이다.

마지막으로 본 논문의 주요 contribution에 대해 정리한다.

Transformer만으로 이루어진 접근법들과 달리 더 높은 차원의 데이터에도 효율적으로 적용할 수 있다.
여러 task(inpainting 등)에서 계산 비용을 크게 감소 시키면서 경쟁력 있는 성능을 달성하였다.
기존 연구는 재구성(reconstruction)과 생성(generative)능력 사이의 차이를 조절하는 것이 중요했지만, 본 논문의 모델은 그것이 필요 없다.
- 두 가지를 분리해서 해결했기 때문이다.
  - Autoencoder는 오직 **재구성(압축과 복원)**만 담당한다.
  - Diffusion 모델은 오직 **이미지 생성(새로운 이미지 합성)**만 담당한다.
초해상도와 같은 고밀도 작업에서도 적용이 가능하다.
cross attention을 기반으로 하는 매커니즘을 개발하여 multi-modal data에도 사용할 수 있다.

Method

Introduction에서도 설명이 되어있듯이, 기존 DM은 pixel space에서 매우 비용이 큰 연산을 수행해야한다는 단점이 있다.

이를 해결하기 위하여 압축과 생성 단계를 분리 하였고, 압축 단계는 계산 비용이 작은 autoencoder를 사용한다.

이를 통해 계산 효율성이 증가하고, 반복적으로 사용할 수 있는 latent space를 제공하여 범용적인 압축 모델이 된다.

또한 본 논문은 UNet의 Inductive bias를 활용하여 공간적 구조를 잘 표현하기 때문에, 과도하게 압축하지 않고도 효과적으로 이미지를 잘 생성해낼 수 있게 된다.

본 논문에서는 UNet 구조를 사용하겠다라는 의미이다.
Inductive bias란?
- Inductive biases: 모델이 학습된 데이터 외의 데이터에 대해 얼마나 잘 일반화할 수 있는지에 사용하는 가정
  - 머신러닝의 최종 목표는 generalization, 즉 학습 데이터로 학습시킨 모델이 본 적 없는 데이터에 대해서도 예측(prediction, approximation)을 잘 해내는 것이다. 본 적 없는 상황을 예측하기 위해서는 학습된 가정 이외에 추가적인 가정이 필요한데, 이것이 바로 inductive bias이다.
- VIT 9번에 나와있는 내용이다.

Perceptual Image Compression

이 파트에선 본 논문에서 AutoEncoder(AE)를 사용하여 perceptual Image compression을 잘 하게 된 배경에 대해서 설명한다.

먼저 AE는 perceptual loss와 patch-based adversarial objective를 사용하여 훈련을 진행한다.

두 가지 방법의 장점이 있다.
첫째로 local realism을 유지하도록 강제하여 재구성된 이미지가 원본 이미지의 분포내에 있게 보장한다.
둘째로 단순한 픽셀 공간의 손실에 의존시 발생하는 흐릿함(bluriness)을 방지한다.

또한 AE의 구조를 설명한다. AE는 $x \in \mathbb{R}^{H \times W \times 3}$ 에 대해:

인코더 $E$는 $x$를 latent representation($z$)으로 변환한다. ($z = E(x)$)
- $E$는 원본 이미지($x$)를 특정 배율 $f$만큼 다운 샘플링을 진행한다.
- 비율은 $f = \frac{H}{h} = \frac{W}{w}$와 같고 본 논문은 $f = 2^m$ 으로 실험을 진행한다.
디코더 $D$는 z에서 다시 원본 이미지를 복원한다. ($\tilde{x} = D(z) = D(E(x))$)
latent representation는 $z \in \mathbb{R}^{h \times w \times c}$에 속한다.

잠재 공간(latent representation)의 과도한 분산 문제를 해결하기 위하여 본 논문은 두 가지 정규화 기법을 도입한다.

첫 번째로 KL-reg이다. 이는 학습된 잠재 표현이 표준 정규 분포를 따르도록 KL-penalty를 부여한다.

두 번째로 VQ-reg이다. 이는 벡터 양자화를 디코더에 포함시켜 양자화 층을 디코더 층에 흡수 시킨다.

이러한 압축 방식들은 기존 방식(VQ-VAE, VQ-GAN)보다 더 낫다. 왜냐하면 기존 방식은 잠재 공간을 1D로 변환해서 자기회귀 방식을 사용한다. 상당한 z의 구조가 무시되는 경향이 있다.

하지만 본 논문은 잠재 공간을 2D 구조로 가져가 구조를 유지한채로 낮은 압축률로도 높은 품질의 이미지를 생성해낼 수 있게 된다.

Latent Diffusion Models

기존의 DM은 변분 하한(variational lower bound) 기반의 재가중치(reweighted)된 변형을 사용한다. 이는 디노이징 스코어 매칭(denoising score-matching) 과 유사한 방식으로 동작한다.
reweighted variant of the variational lower bound란?
- 학습 효율성을 높이기 위해 특정 $t$ 단계(예: 중간 정도의 노이즈)에 noise schedule을 조절하여 더 높은 가중치를 부여하는 방식이다.
- 난 노이즈 스케줄 조정 = 특정 스텝 가중치 조정 = Reweighting으로 이해했다.

본 논문은 이 DM을 디노이징 오토인코더(denoising autoencoders) $\epsilon_\theta(x_t, t)$들의 동일한 가중치를 가진 연속적인 집합으로 볼 수 있다고 설명한다. 아래는 이런 DM의 간단한 목적식을 나타낸 것이다.

이때 이 오토인코더는 노이즈가 포함된 $x_t$에 대해 디노이징된 $x_\text{t-1}$을 예측하도록 학습된다.

$$L_\text{DM} = \mathbb{E_{x, \epsilon \sim \mathcal{N}(0,1), t}} \left[ \left| \epsilon - \epsilon_ {\theta}(x_t, t) \right|_2^2 \right]$$

본 논문에선 perceptual compression 모델인 AE를 사용하여 효율적인 저차원 latent space를 얻게 된다.

반복적인 얘기지만, AE를 사용하면 pixel-based와 비교했을 때 데이터의 중요한 semantic적인 요소에 집중할 수 있다.
또한 저차원의 공간을 사용하면서, 계산 효율성이 증대된다.

기존에 latent space에서 autoregressive 및 transformer 기반의 모델을 사용한 반면, 본 논문은 UNet구조로 2D Conv 구조를 중심으로 가져간다.

UNet 구조를 채택하여 이미지 특화된 inductive bias를 활용할 수 있다. 또한 이를 활용하여 재가중치된 변분 하한을 사용하여 지각적으로 중요한 정보에 집중할 수 있게 된다.

따라서 아래는 본 논문에서 제안하고 있는 목적식을 나타낸 것이다.

$$L_{LDM} := \mathbb{E_{\mathcal{E}(x), \epsilon \sim \mathcal{N}(0,1), t} }\left[ \left| \epsilon - \epsilon_{\theta}(z_t, t) \right|_2^2 \right].$$

기존 DM 목적식과 다른 것은 인코더 $\mathcal{E}(x)$ 를 통해 나온 $z_t$가 denoising 모델인 $\epsilon_{\theta}(z_t, t)$의 input으로 들어간다는 점이다.

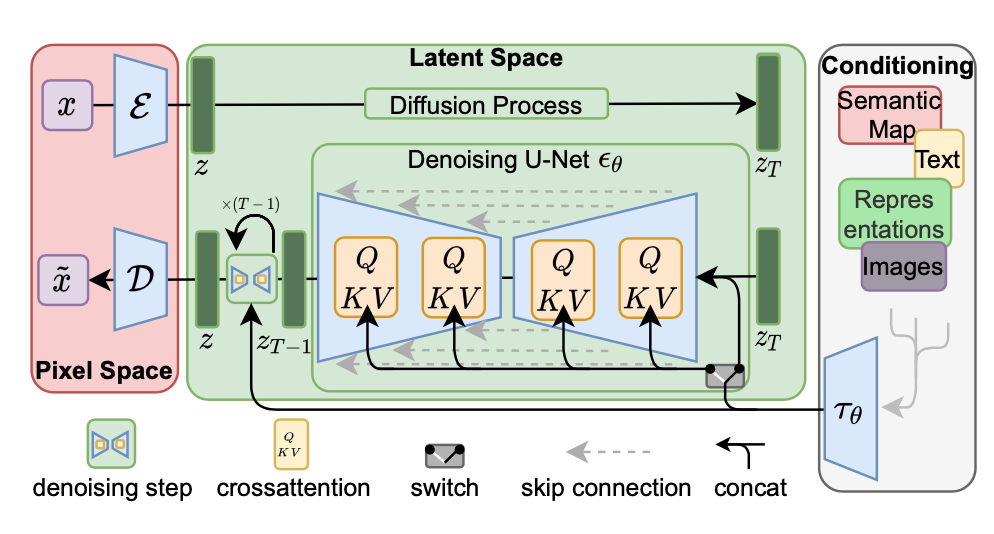
위 사진은 본 논문의 전체적인 구조를 나타내고 있다.

forward pass는 고정되어 있기 때문에 학습 시 $z_t$ 를 효율적으로 얻을 수 있고, 샘플링 시 에도 $p(z)$ 에서 샘플을 뽑아 디코더 $D$의 single pass로 이미지 복원이 가능하다.

Conditioning Mechanisms

다른 생성 모델과 마찬가지로 DM은 조건부 확률 분포로 이루어질 수 있다. ($p(z|y)$)

이를 구현하는 방법은 conditional denosing autoencoder $\epsilon_\theta(z_t, t, y)$를 사용하는 것이다.

이를 통해 입력 $y$가 다양한 task에 사용될 수 있게 된다.

본 논문에서는 conditional DM을 만들기 위해 Unet에 cross-attention mechanism을 부착한 구조를 제안한다.

그렇게 하기 위하여 domain-specific encoder($\tau_\theta$) 를 도입한다. $\tau_\theta(y)$는 UNet의 중간 표현의 cross-attention layer를 통해 연결 된다.

아래는 cross-attention에 condition을 적용하는 식이다.

$$ \text{Attention}(Q,K,V) = \text{softmax} \left( \frac{QK^T}{\sqrt{d}} \right) \cdot V \\ \textbf{쿼리(Query)}: ( Q = W_Q^{(i)} \cdot \varphi_i(z_t) ) \\ \textbf{키(Key)}: ( K = W_K^{(i)} \cdot \tau_{\theta}(y) ) \\ \textbf{값(Value)}: ( V = W_V^{(i)} \cdot \tau_{\theta}(y) ) $$

$ \varphi_i(z_t) \in \mathbb{R}^{N \times d_{\epsilon}^{i}}$ 는 UNet에서 Flatten된 중간 표현을 의미한다.
- 더 쉽게 설명하자면, 기존의 DM에서 시간 $t$에서 추출된 표현($z_t)$을 attention mechanism에 적용하기 위하여 Flatten한 것이다.
  
  Query에만 $\varphi_i$가 곱해지는 이유?
  - `Cross-attention`에서 `쿼리(Q)`는 모델이 주어진 입력을 기반으로 **어텐션을 적용할 요소를 결정하는 역할**이다. - 즉, `쿼리(Q)`는 `DM`이 현재 생성 중인 **이미지의 정보를 포함하는 특징 맵(feature map)**이 되기 때문에 쿼리에 $\varphi_i$를 곱하는 것이다.

아래는 본 논문에서 제안하는 LDM의 최종 목적식이다.

$$L_{LDM} := \mathbb{E_{\mathcal{E}(x), y, \epsilon \sim \mathcal{N}(0,1), t} }\left[ \left| \epsilon - \epsilon_{\theta}(z_t, t, \tau_\theta(y)) \right|_2^2 \right].$$

기존 모델에 condition을 부여할 수 있게 $y$와 학습 가능한 $\tau_\theta$가 추가되어 있는 것을 볼 수 있다.

Experiments

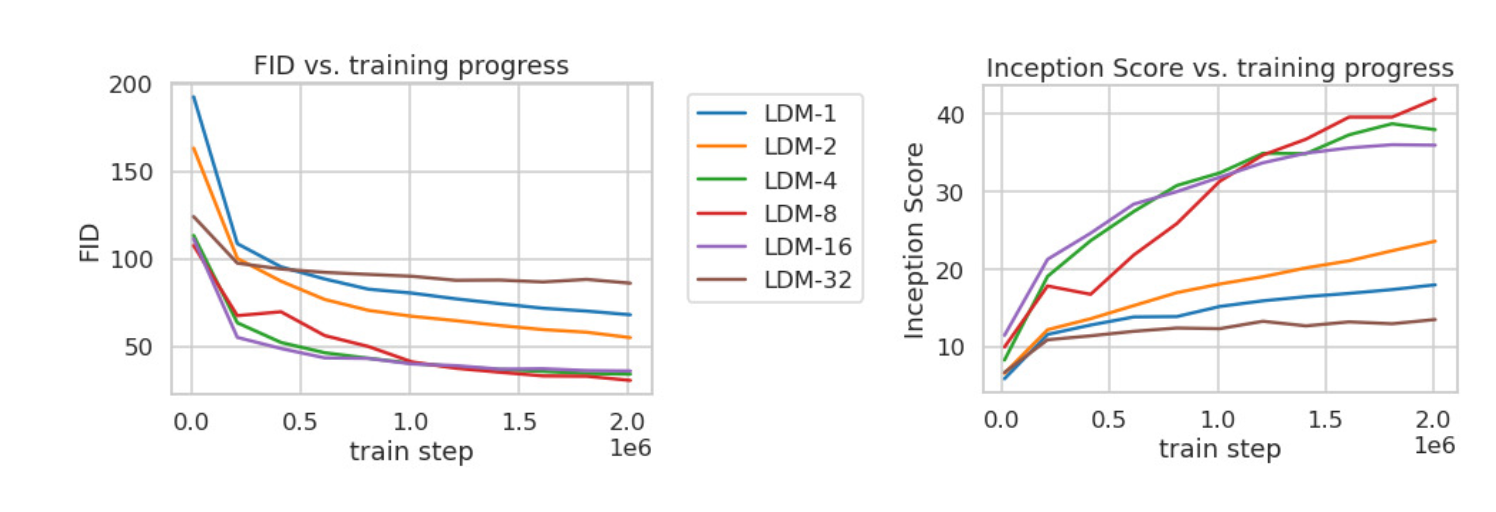
위 그래프는 ImageNet을 학습 할 때 step에 대한 샘플 품질(FID, IS)를 나타낸다.

작은 downsampling factor는 학습을 느리게 하는 것을 확인 할 수 있다.
큰 factor는 비교적 적은 step에서 샘플 품질이 정체가 되는 것을 확인 할 수 있다.

FID Score란?
- `FID(Fréchet Inception Distance) Score`는 `생성된 이미지`와 `실제 이미지` 간의 **품질 차이**를 측정하는 평가 지표이다. - `실제 데이터셋`과 `생성된 이미지`의 `특징 벡터`를 추출하여, 두 분포의 `평균`과 `분산`을 계산하고 두 정규 분포 간의 **Fréchet Distance (Wasserstein-2 거리)**를 구한다. - `FID Score` **값이 낮을수록** 더 좋은 성능을 의미한다. -

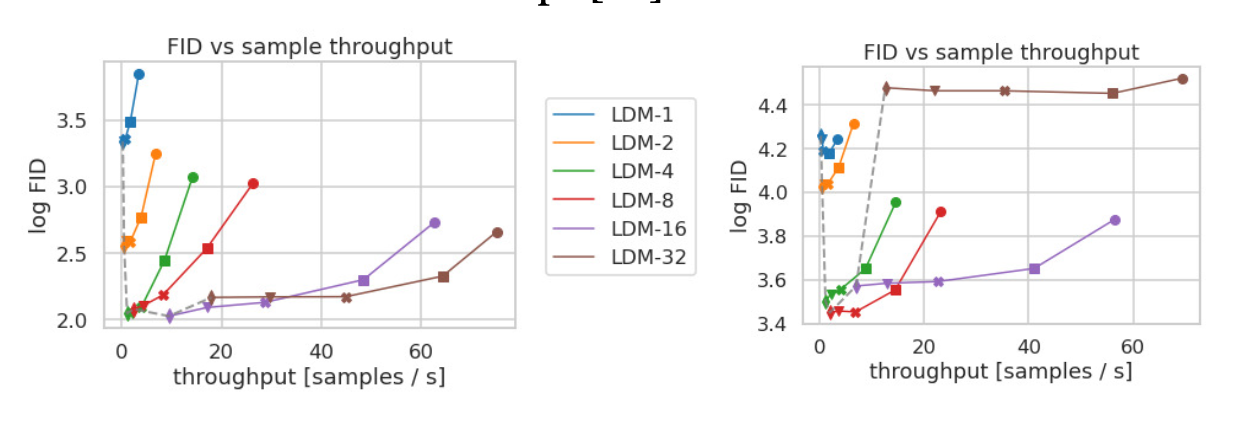
위 그래프는 CelebA-HQ와 ImageNet으로 학습한 LDM의 샘플링 속도와 FID를 비교한 그래프이다.

LDM-4, LDM-8이 성능이 제일 좋다는 것을 알 수 있게 된다.

LDM은 기존 DM, 생성 모델들 대비 좋은 성능을 내보였으며 여러 Task에서도 좋은 성능을 보였다.

Limitation

LDM은 Pixel-based 방법과 비교하여 계산량을 줄일 수 있지만 샘플링 과정이 순차적으로 이루어지기 때문에 GAN보다는 속도가 느리다.

또한 High Precision을 원할 경우 LDM의 활용이 제한될 수 있다.

본 논문에서 제안한 $f = 4$인 AE의 경우에 loss가 매우 작다.
하지만 픽셀 수준에서의 정밀한 복원이 필요한 작업에서는 재구성 성능(reconstruction capability)이 병목(bottleneck)이 될 수도 있다.

또한 논문에서는 생성 모델에 대한 문제점에 대해서 설명하고 있다.

조작된 데이터의 생성을 할 수 있는 사회적 영향 문제
학습 데이터 유출 가능성이 있는 데이터 프라이버시 문제
DM은 데이터 분포를 그대로 학습하기 때문에 학습 데이터에서 분포가 충분하지 않거나 편향되어있다면 생성 데이터에 대한 정당성 또한 편향적일 수 있는 편향(bias)문제