[Paper Review]Generative Adversarial Nets(GAN)

GoodYoung included in Paper Review DL

2024-09-02 1283 words 7 minutes

Contents

개요

VAE논문 다음으로 Generative분야에서 기초가 되는 논문인 GAN에 관한 리뷰를 할 것이다.

Introduction

다양한 data환경에서 확률 분포를 잘 표현할 수 있는 풍부하고 계층적인 모델을 발견하는 것이 딥러닝의 잠재력이다.

딥러닝의 두드러진 성공 사례는 풍부한 감각 input을 class label로 매핑하는 판별 모델이다.

이런 성공은 backpropagation과 dropout의 algorithm, gradient를 가진 조각별 선형적 유닛들(ReLU)에 기반을 두고 있다.

그동안 Deep generative model은 큰 영향을 끼치진 못했다. Likelihood에 대한 추정과 관련된 전략에서 발생하는 계산을 근사화하는 것이 어렵고, 조각별 선형적 유닛들을 활용하여 generative에서 활용하는 것도 어렵기 때문이다.

따라서 본 논문은 이런 어려움들을 피할 수 있는 추정 절차를 제안한다.

제안된 adversarial nets은 generative model은 discriminative model과 맞서게 된다.

Discriminative model은 model 분포에서 나온 것인지 data 분포에서 나온 것인지 구분하는 방법을 학습한다.

Generative model은 위조자와 비슷하게 생각할 수 있다. 이는 fake 지폐를 만들어 경찰의 탐지 없이 사용하려고 한다. 반면 discriminative model은 경찰에 비유할 수 있다. 이런 fake 지폐를 탐지하려고 한다.

이런 상황 속에서 두개의 model이 자신들의 방법을 개선하려고 한다. 결국 위조지폐가 진짜 지폐와 구별되지 않게 되게 된다.

이 framework는 다양한 모델과 최적화 방법에 대해서 특정한 training algorithm을 도출할 수 있다.

Generative 모델이 MLP을 통해 random noise를 통과시켜 sample을 생성하는 특수한 경우를 탐구합니다. 이런 특수한 경우를 적대적 신경망(Adversarial Nets)이라고 부른다.

Generative, discriminative model 둘 다 backpropagation을 통하여 업데이트를 하며 generative model을 통하여 sampling을 할 땐 forward만 수행한다.

Adversarial nets

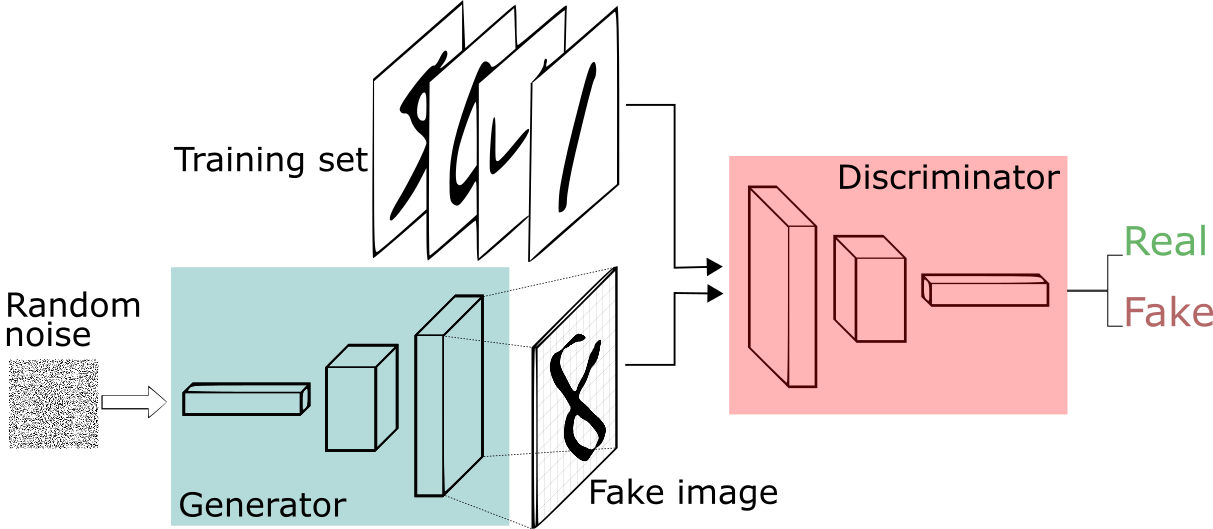
이젠 Adversarial nets에 대한 설명을 할 것 이다. Adversarial modeling framework는 both multilayer perceptron 일 때 곧바로 적용할 수 있다.

Data x에 $p_g$ 분포를 배우기 위하여 사전에 noise 변수 $p_z(z)$를 선언한다. 그 후 $G(z;\theta_g)$의 data space에 매핑을 하게 된다.

이 때 $G$는 파라미터 $\theta_g$를 지닌 미분 가능한 함수이다.

또한 두번째 multilayer perceptron이고 output이 하나의 scalar가 나오는 $D(x;\theta_d)$가 있게 된다. 이때 $D(x)$는 $p_g$분포와는 다른 $x$로부터 나왔을 확률을 representation한다.

이때 나온 output(single scalar)이 1: real ~ 0: fake일 확률을 나타낸다.

본 논문에서 나오는 훈련은 $D$는 훈련 샘플과 $G$에서 나온 샘플 (fake image) 모두에 대해 올바른 label(real or fake)을 할당하는 확률을 최대화하도록 훈련이 된다.

또 동시에 $G$를 $log(1-D(G(z))$ 를 사용하여 최소화 하는 방식으로 훈련을 하게 된다.

위의 내용을 총 정리한 $V(G,D)$ 의 목적 함수(Object Function)를 나타내면 아래의 식이다.

$$\min_G \max_D V(D, G) = E_{x \sim p_{\text{data}}(x)} [\log D(x)] + E_{z \sim p_z(z)} [\log(1 - D(G(z)))]$$

위의 Adversarial net을 나타내는 목적 함수를 좀 더 살펴 보도록 할 것 이다.

$\min_G \max_D V(D, G)$ 의 부분을 먼저 살펴보자면 $V(D, G)$ 식에서 $G$ 는 낮추고자 하고 $D$ 는 높이고자 하는 것을 알 수 있다.

$D$의 목표는 진짜 데이터에 대해 높은 확률을 부여하고 가짜 데이터에 대해 낮은 값을 부여하도록 하는 역할이기 때문에 최대화를 목표로 한다.
$G$의 목표는 생성된 데이터가 $D$에게 진짜 데이터 처럼 보이게 하는 역할이기 때문에 최소화를 목표로 한다.

$E_{x \sim p_{\text{data}}(x)} [\log D(x)]$ 은 원본 데이터 $p_\text{data}(x)$에서 한개의 데이터인 $x$를 sampling을 하여 그 $x$를 $D$에 넣은 값에 $log$를 취한 값의 기대값을 나타낸다.

따라서

앞서 13번을 보면 사전에 noise 변수인 $p_z(z)$ 를 선언한다고 나와 있다.

따라서 $E_{z \sim p_z(z)} [\log(1 - D(G(z)))]$ 의 식은 하나의 noise 분포 $p_z(z)$ 에서 한 값을 sampling하여 그 $x$ 를 생성자 $G$ 에 넣고 가짜 이미지를 만든 다음에 $D$에 넣고 $1-D$의 형태로 만든 값에 $log$를 취한 값의 기대값을 나타낸다.

그래서 이런 두 항을 $D$의 관점에서 봤을 때 maximize하기 때문에 원본 데이터(x)에 대해서는 real(1)을 찾을 수 있도록 하고 반면에 가짜 이미지(z)가 들어왔을 때는 그 이미지가 fake(0)인지 분류할 수 있게 가능하게 한다.

생성자 $G$는 이 $E_{z \sim p_z(z)} [\log(1 - D(G(z)))]$ 항을 minimize하기 때문에 다음과 같이 해석을 할 수 있게 된다.

noise 분포에서 뽑은 가짜 이미지가 판별자에 의해서 진짜(1)라고 내뱉을 수 있도록 학습을 하는 것이다.

$G$가 그럴싸한 이미지를 만들 수 있도록 학습을 하는 것이다.

Theoretical analysis of adversarial nets

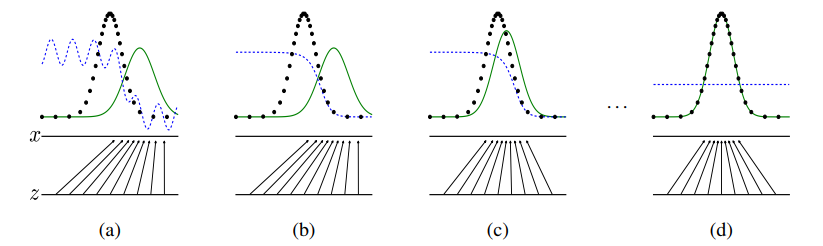
다음은 Adversarial net의 이론적 분석을 제시한다. Non-parametric limit인 상황에서 이 Net의 훈련 기준은 $G$와 $D$가 충분하게 있을 때 data를 generating하는 기능을 하게 된다.

이때 나온 Non-parametric상황은 특정한 매개변수 수에 제한되지 않는다는 것을 의미하게 된다.
- 즉, 임의의 복잡한 함수도 근사할 수 있는 충분한 유연성을 가진 경우를 의미한다.

$D$를 최적화 하는 단계를 k번 반복하고, $G$를 최적화하는 단게를 한 번 수행하게 된다.

$G$가 충분히 천천히 변하는 동안 $D$가 optimal한 solution을 지니도록 한다.

위 그림은 해당 학습 과정에 데이터 분포를 그림으로 표현한 것이다. 파란색 점선 : discriminative distribution(데이터 구분), 검은색 점선 : data generating distribution $p_x$(실제 데이터), 녹색 실선 : generative distribution $p_g$(생성한 데이터)이다.

또한 밑에 수평선 $z$는 $z$가 샘플되는 영역(domain)을 나타낸다.
이때 z->x로 향하는 화살표들은 mapping x = G(z)가 non-uniform한 분포 p_g를 transformed samples로 변경하게 된다.

각 단계에 대한 설명을 할 것이다. a: 학습 초기 단계이다. 그림을 보면 discriminative distribution이 부분적으로 정확한 classifier인 상태이다.

b: $D$가 $D*(x) = p_data(x)/((p_data(x) + p_g(x))$로 수렴하여 실제 데이터와 생성된 가짜 데이터를 구분할 수 있게 학습이 된 상태이다.

c: $G$를 학습시킵니다. 이때 $D$의 그래디언트는 $G(z)$가 실제 데이터와 같은 데이터로 변형되게 변하는 상태를 볼 수 있다.

d: $G$와 $D$가 충분한 능력을 가질 때까지 a~c를 여러번 반복합니다. $G$는 $p_g = p_data$라고 할 정도로 데이터를 잘 생성하는 것을 확인할 수 있다. 또한 $D$는 두 데이터의 차이를 구분할 수 없게 되었다. 즉, D(x) = 0.5입니다.

0.5인 이유는 훈련이 잘 되었을 때 $D$가 실제인지 가짜인지 50%의 확률로 추정하기 때문이다.

위 그림은 위의 단계들을 pseudo code로 각 step을 나타낸 그림이다.

결론적으로 adversarial net의 목적 함수들의 최종 목표를 정리하자면 $p_g -> p_\text{data}$ 이다. 생성자의 분포가 원본 학습데이터의 분포를 잘 따를 수 있도록 만드는 것이다.

또한 $D(G(z)) -> 1/2$이다. $D$가 더이상 가짜 데이터와 진짜 데이터를 구분할 수 없기 때문에 $1/2$로 가게 되는 것이다.

Global Optimality

다음은 실제로 학습을 진행했을 때 $p_g -> p_\text{data}$ 로 진행하는지에 대해서 증명을 할 것이다.

매 상황에서 $D$와 $G$가 어디서 global optimal을 가지는지에 대해서 나타낼 것이다.

$G$가 고정되어 있을 때 $D$의 optimal point는 아래 식과 같다.

$$D_G^*(x) = \frac{p_\text{data}(x)}{p_\text{data}(x) + p_g(x)}$$

이제 위 식이 어떻게 나왔는지에 대해서 증명을 할 것이다.

$V(G,D)$를 변경을 하면 아래 식과 같아진다. $$V(G, D) = E_{x \sim p_{\text{data}}(x)} [\log D(x)] + E_{z \sim p_z(z)} [\log(1 - D(G(z)))]$$ $$= \int_x p_{\text{data}}(x) \log(D(x))dx + \int_z p_z(z) \log(1 - D(G(z)))dz \ (\therefore E[X] = \int_{-\infty}^{\infty} x f(x)dx )$$

그리고 식을 조금 더 정리를 하게 되면 아래 식과 같아진다. $$= \int_x p_{\text{data}}(x) \log(D(x)) \dx + \int_x p_g(x) \log(1 - D(x))dx$$

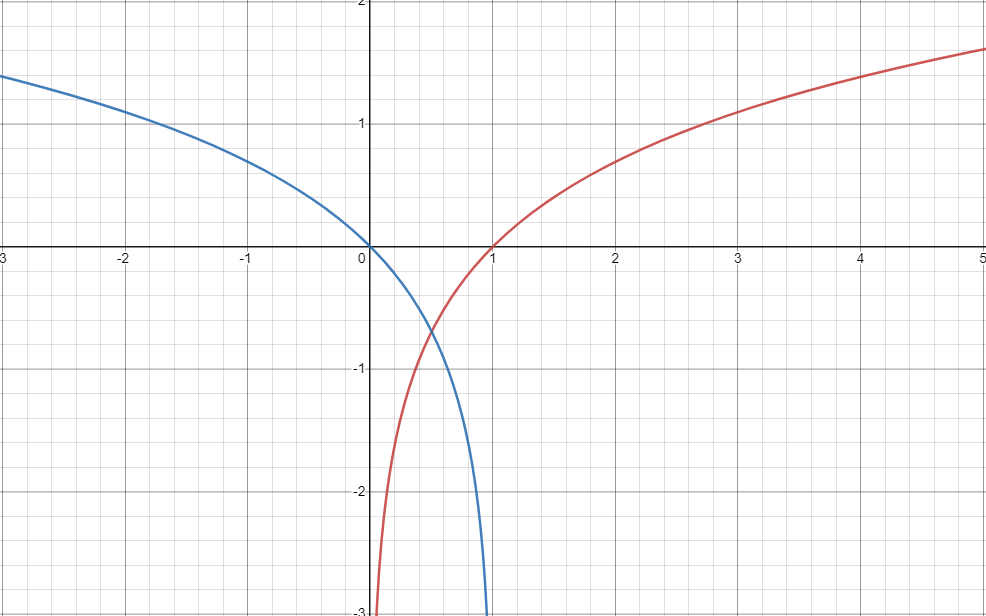
이때 $alog(y) + blog(1-y)$ 의 형태일 때 $\frac{a}{a+b}$ 에서 global optima를 가진다는 정리를 이용하게 되면 $D_G^*(x)$의 식이 나오게 되는 것이다.

이제 $G$의 global optima point를 구하려고 한다.

아래는 고정된 $G$에 대해서 $V$함수를 최대로 만드는 $D$에 대한 함수 이다. 이는 Global optima를 가지는 $D$함수에 대한 $V$함수로 정의가 가능하다. $$C(G) = max_D V(G, D) = E_{x \sim p_{\text{data}}(x)} [\log (D^*(x))]+ E_{z \sim p_z(z)} [\log(1 - D^*(G(z)))]$$
- $D^*$로 $D$는 이미 optima하게 되어있는 것을 확인 할 수 있다.

위 식의 $D$를 풀어서 작성하면 아래 식과 같다. $$= E_{x \sim p_{\text{data}}(x)} \left[ \log \frac{p_{\text{data}}(x)}{p_{\text{data}}(x) + p_g(x)} \right] + E_{x \sim p_g(x)} \left[ \log \frac{p_g(x)}{p_{\text{data}}(x) + p_g(x)} \right](\therefore D_G^*(x) = \frac{p_\text{data}(x)}{p_\text{data}(x) + p_g(x)})$$

식 변형을 위하여 식에 2를 곱하고 $log(4)$를 빼준다. $$= E_{x \sim p_{\text{data}}(x)} \left[ \log \frac{2 \cdot p_{\text{data}}(x)}{p_{\text{data}}(x) + p_g(x)} \right] + E_{x \sim p_g(x)} \left[ \log \frac{2 \cdot p_g(x)}{p_{\text{data}}(x) + p_g(x)} \right]-log(4)$$

이 식은 다시 KL-divergence로 변형할 수 있다. $$= KL\left(p_{\text{data}} \bigg| \frac{p_{\text{data}}(x) + p_g(x)}{2} \right) + KL\left(p_g \bigg| \frac{p_{\text{data}}(x) + p_g(x)}{2} \right) - \log(4) (\therefore KL(p_{\text{data}} | p_g) = \int_{-\infty}^{\infty} p_{\text{data}}(x) \log \left( \frac{p_{\text{data}}(x)}{p_g(x)} \right) dx)$$

이는 다시 $JSD$로 변환이 가능했다.

KL-divergence는 두개의 분포가 수치적으로 얼마나 차이가 나는지에 대해서 일반적으로 사용할 수 있는 공식이다.
Jsd는 KL-divergence는 distance matrix로 활용하기 어렵기 때문에 JSD방법론을 사용하게 된다.
- 두개의 분포가 있을 때 두 분포의 distance를 구하는데 사용이 된다.

$$= 2 \cdot JSD(p_{\text{data}} | p_g) - \log(4)(\therefore JSD(p | q) = \frac{1}{2} KL\left(p \bigg| \frac{p + q}{2}\right) + \frac{1}{2} KL\left(q \bigg| \frac{p + q}{2}\right))$$

위 식은 이 JSD 분포는 최솟값으로 0의 값을 가지게 된다. 따라서 최종적으로 최솟값으로 $-log(4)$로 얻는다.

그래서 이러한 최솟값을 얻을 수 있게 하는 것은 $p_data$와 $p_g$가 동일할 때를 의미한다.

따라서 30번 라인을 보면 $D$가 수렴을 한 후에 $G$를 학습시켜 $G$도 수렴하게 가중치 업데이트를 수행하게 되는 것을 알 수 있다.

Experiment

위의 훈련 결과를 보면 노란색 박스가 훈련 중 가장 가까운 sample을 뽑은 것이다. 이를 보면 왼쪽과 확연히 다른 것을 확인 할 수 있는데 이는 모델이 훈련 시 memorized하지 않았다는 것을 의미한다.