GoodYoung Dev Blog
Posts Tags Categories
GoodYoung Dev Blog

Contents

[Paper Review]Denoising Diffusion Probabilistic Models(DDPM)

GoodYoung included in Paper Review DL Diffusion
   2183 words   11 minutes 

개요

  1. Diffusion의 기초인 DDPM에 대한 논문을 리뷰할 것이다.

Introduction

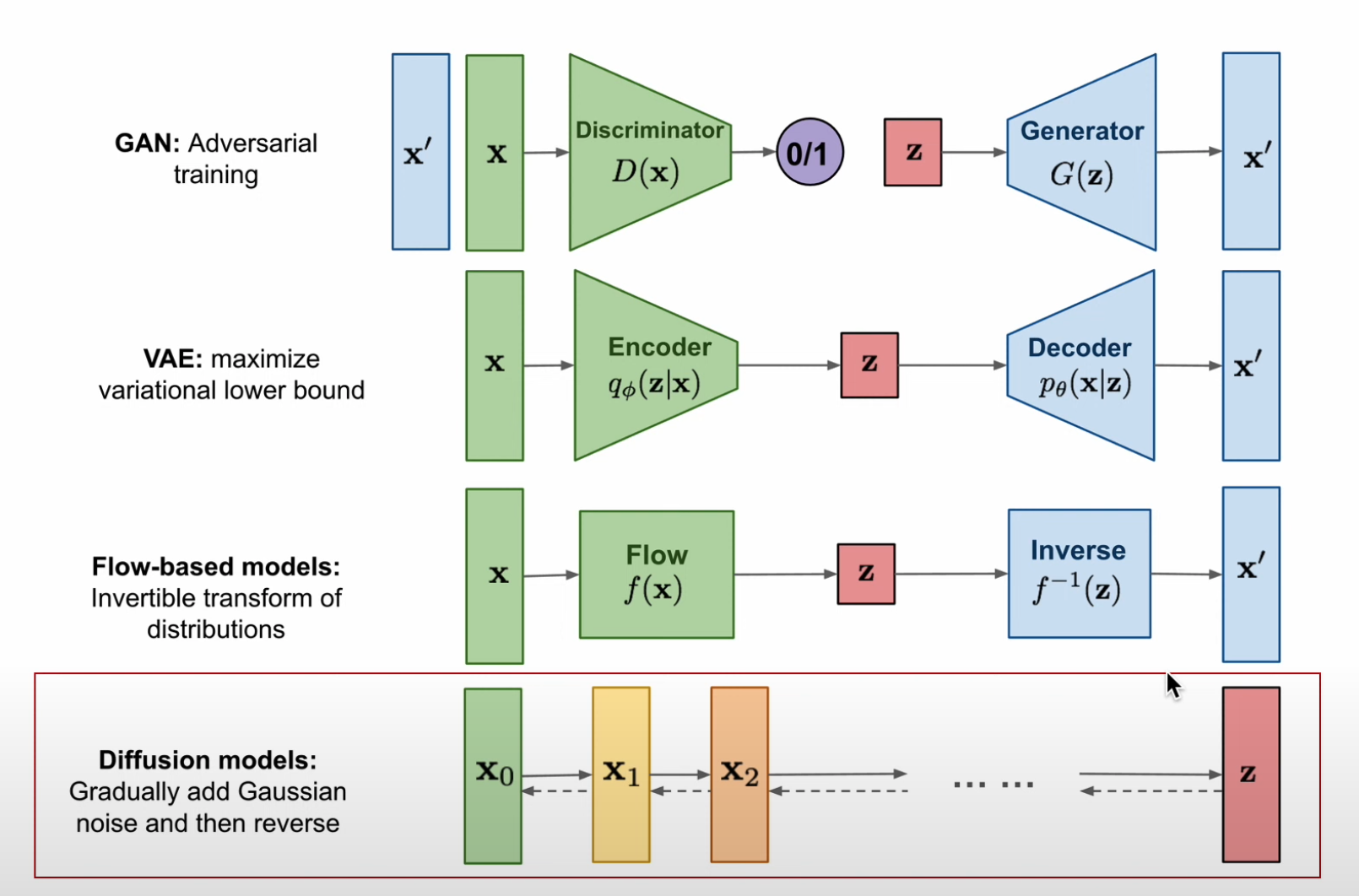
  1. 최근 몇 년간 다양한 생성 모델(deep generative models) 이 높은 품질의 샘플을 생성하는 성과를 보였다.

  1. 에너지 기반 모델(Energy-Based Models) 및 Score Matching 기법도 GAN과 비슷한 수준의 이미지 품질을 생성하는 연구가 등장했다.

  1. 이 논문은 Diffusion Probabilistic Models의 발전이다.
  • Diffusion Probabilistic Models (DPMs, 2015): Markov chain을 기반으로 데이터를 점진적으로 샘플링하는 모델
Markov Chain이란? - 어떤 시간에 특정 state에 도달하든, 그 이전에 어떤 state를 거쳐왔든 다음 state로 갈 확률은 항상 같다는 성질이다.

  1. DPMs는 변분 추론을 활용해 샘플을 생성하기 위해 **확산 과정(diffusion process)을 반전(reverse)**시키는 방법을 학습한다.
  • 변분 추론(variational inference) : 확률 모델에서 복잡한 후행 확률 분포(posterior distribution)를 근사하는 방법 중 하나이다.
    • 정확한 posterior를 계산하는 것은 intractable하여 $p(z|x)$를 계산하는 것 대신 $q_\theta(z|x)$로 근사하는 방법이다.
  • 즉, 변분 추론을 통해 모델의 역방향 과정의 확률 분포( $p(x_\text{t-1} | x_t)$ )를 근사하여, $p_\theta(x_\text{t-1} | x_t)$ 를 통하여 정방향 과정에서 추가된 노이즈를 제거하는 방법을 학습

  1. DPMs은 정의하기 쉽고 학습이 효율적이지만, 지금까지 고품질 샘플을 생성할 수 있다는 실증적인 연구가 부족했다.
  • 하지만 이 논문(DDPM)에서 DPMs이 고품질 샘플을 생성하고, 때때로 다른 모델보다 더 좋은 성능을 보인다.

  1. DDPM을 특정 방식으로 파라미터화 하면 다중 노이즈 수준에서 Denoising Score Matching과 동일하며, Annealed Langevin Dynamics와도 유사한 샘플링 방식을 갖는다는 점을 발견 한다.
  • 46번에서 자세하게 설명을 한다.

  1. DDPM도 샘플의 품질은 뛰어나지만, log-likelihood 기반 모델들과 비교했을 때 경쟁력 있는 성능이 존재하진 않는다.
  • Loss 중 많은 부분이 눈에 보이지 않는 미세한 이미지 세부 정보를 설명하는데 사용이 된다.
  • log-likelihood model : VAE, Normalizing Flows, Autoregressive Models
    • log 가능도를 최대화 하는 모델들

Background

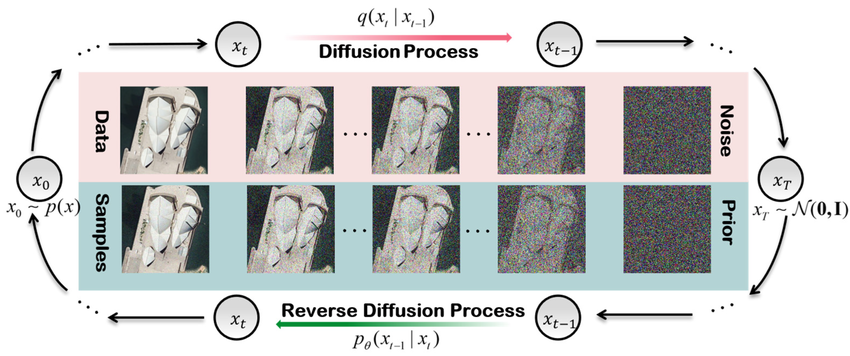
  1. 4번에서 DPMs는 정방향 과정에서 추가된 노이즈(destroy)를 제거하는 방법을 학습하는 과정을 수행한다고 설명하였다.
  • 물리학적으로 미세한 세계에서는 destroy된 상태를 backward로 복원시키는 것이 가능하다.

  1. DDPM에서는 노이즈를 점차 추가하여 destroy하는 정방향 과정을 diffusion process이라고 한다.

  1. 또한, 노이즈를 제거(denoising)하여 다시 복원하는 확률 분포(노이즈)를 학습하는 과정을 reverse process라고 한다.

Diffusion Process

  1. Diffusion Process에 대해서 먼저 간단한 설명을 해보려고 한다.

$$ q(x_\text{1:T} | x_0) := \prod_\text{t=1}^T q(x_t | x_\text{t-1}), \quad q(x_t | x_\text{t-1}) := \mathcal{N}(x_t ; \sqrt{1 - \beta_t} x_\text{t-1}, \beta_t I) $$

  1. Diffusion Process의 근사 후행 확률은 $q(x_\text{1:T}|x_0)$ 으로 나타낼 수 있으며, 이는 마르코프 연쇄(Markov Chain)로 정의되어 이 과정에서 step마다 가우시안 노이즈를 추가하는 방식으로 작동한다.

  1. 이때 노이즈는 $\beta_1, … ,\beta_T$ 의 형태인 variance schedule에 따라 조절된다.

  1. $\beta_t$ 는 reparameterization trick에 의해서 학습이 될 수도 있고, 하이퍼파라미터로 고정될 수 있다.

  • 다음은 $\beta_t$ 에 대하여 reparameterization trick을 적용한 것을 알아본 것이다.

    $\beta_t$에 대하여 reparameterization trick을 적용 한 경우

    • $\beta_t$ 를 gaussian 분포에서 샘플링하는 확률적 변수로 설정한다면:

      $\beta_t = \sigma(\tilde{\beta_t}),\qquad \tilde{\beta_t} \sim \mathcal{N}(\mu_\beta, \sigma_\beta^2) $

      • $\tilde{\beta_t}$ : 가우시안 분포에서 샘플링 된 값
      • $\sigma(\cdot)$ : activation function을 활용하여 $\beta_t$가 양수임을 보장
      • $\mu_\beta, \sigma_\beta $ : 학습 가능한 파라미터

    • 위 식의 $\tilde{\beta_t}$ 을 gaussian 분포에서 직접 샘플링 하기 때문에 이는 확률적 연산이 포함되므로 미분이 불가능해진다.

      • 미분이 불가능해지면 손실 함수의 그라디언트를 계산할 수 없게 된다. (학습 불가능)

    • 그렇기 때문에 미분 가능해지기 위하여 $\beta_t$ 에 gaussian 분포에서 직접 샘플링하는 대신, 표준 정규 분포에서 샘플링한 후, 변형하는 방법인 reparametrization trick의 방법을 사용한다.

    • 해당 방법을 사용하면 다음과 같이 표현 될 수 있다:
      $\tilde{\beta_t} = \mu_\beta + \sigma_\beta \cdot \epsilon, \quad \epsilon \sim \mathcal{N}(0, 1)$

    • 이제 확률적 연산을 결정적 연산으로 변경하여 $\tilde{\beta_t}$ 를 샘플링하는 과정이 미분 가능해졌다.

    • 따라서 경사 하강법(Gradient Descent)을 사용하여 $ \mu_\beta $와 $ \sigma_\beta $ 를 학습할 수 있게 된다.


  1. $\beta_t$ 가 매우 작을 때 diffusion process 와 reverse process에서 모두 gaussian 분포를 따르게 되어 동일한 수식 형태를 유지 할 수 있다.
  • diffusion process에서 결국 $\beta_T$ 시점에 가면 gaussian 분포랑 같게 형성이 된다.
  • reverse process에서 gaussian 분포를 유지하며 근사가 가능해진다.
    • 그렇게 되면 reverse process에서 diffusion process를 예측하기 쉬워지게 된다.

  1. 그리고 $\beta_t$ 를 learnable parameter로 둘 수 있지만, 실험을 해보니 constant로 두어도 큰 차이가 없어서 constant로 두었다. (Forward process and L_T ,Experiment 부분)

  • 초기의 $\beta_t$ 의 값을 작게 설정하다가 T가 증가할수록(= gaussian distribution 에 가까워질수록) 값을 크게 설정한다. (linear하게 증가)

  • 본 논문에선 constant로 설정하여도 $x_T$ 시점에서 pure isotropic gaussian을 확보할 수 있다고 주장한다.

    Pure Isotropic Gaussian이란?
    • 평균 $\mu$ 가 0인 경우, 공분산 행렬이 $\sum = \sigma^2I$ 형태로 주어지며, 모든 차원의 분산이 동일하고 독립적인 경우이다.
      • 등방성(방향성이 없음)이 유지가 된다.
    • 즉, 분포가 표준 가우시안 $\mathcal{N}(0,\mathcal{I})$ 형태를 가질 때를 나타낸다.

  • 이 때문에 reverse process를 시작할 때 사전 분포(prior distribution)이 $\mathcal{N}(0,\mathcal{I})$ 로 설정되어 gaussian 분포를 유지하게 된다.


  1. 또한, $q(x_\text{1:T}|x_0)$ 을 위 식 그대로 $\beta_t$로 계산하게 되면 문제점이 있다.

  1. $x_0$(original image)에서 $x_T$(noisy image)로 전개될 때, 0~T의 모든 수식을 step by step으로 전개해야된다.
  • 이는, memory를 많이 소모하며, 시간이 오래걸리는 단점이 있다.

$$\alpha_t := 1 - \beta_t ,\quad \bar{\alpha_t} := \prod_\text{s=1}^{t} \alpha_s$$

$$q(x_t \mid x_0) = \mathcal{N}(x_t; \sqrt{\bar{\alpha}_t} x_0, (1 - \bar{\alpha}_t) \mathbf{I})$$

  1. 그렇기 때문에 $q$ 의 식을 위와 같은 수식으로 변경하여 폐쇄형 해(closed-form solution)으로 샘플링 가능하기 때문에 임의의 시간 $t$ 에서 샘플링 $x_t$를 직접 계산할 수 있게 된다.

  • 이렇게 일반화 식을 만들면 stochastic gradient descent을 이용하여 효율적인 학습이 가능하다.

    폐쇄형 해(closed-form solution)이란?
    • 어떤 수학적 문제의 해(해결 방법)를 유한한 개수의 기본 연산(+, -, ×, ÷, √, exp, log 등)으로 정확하게 표현할 수 있는 경우
    • 수식을 직접 계산할 수 있는 형태
    증명 확인 $ \begin{aligned} q(x_t \mid x_{t-1}) &= \mathcal{N}(x_t; \sqrt{1 - \beta_t} x_{t-1}, \beta_t I) \text{이므로 reparametrization trick을 사용한다면} \end{aligned} $ $$ \begin{aligned} x_t &= \sqrt{1 - \beta_t} x_{t-1} + \sqrt{\beta_t} \epsilon_{t-1} \quad &(\epsilon_{t-1} \sim \mathcal{N}(0, I)) \\\\ &= \sqrt{\alpha_t} x_{t-1} + \sqrt{1 - \alpha_t} \epsilon_{t-1} \\\\ &= \sqrt{\alpha_t} (\sqrt{\alpha_{t-1}} x_{t-2} + \sqrt{1 - \alpha_{t-1}} \epsilon_{t-2}) + \sqrt{1 - \alpha_t} \epsilon_{t-1} \quad &(\epsilon_{t-2} \sim \mathcal{N}(0, I)) \\\\ &= \sqrt{\alpha_t \alpha_{t-1}} x_{t-2} + \sqrt{(1 - \alpha_{t-1}) \alpha_t} \epsilon_{t-2} + \sqrt{1 - \alpha_t} \epsilon_{t-1} \\\\ \end{aligned} $$ $ \begin{aligned} \alpha_t (1 - \alpha_{t-1}) + 1 - \alpha_t = 1 - \alpha_t \alpha_{t-1} \text{이므로} (1 - \alpha_t \alpha_{t-1}) I \text{이고 대입하면,} \end{aligned} $ $$ \begin{aligned} x_t &= \sqrt{\alpha_t \alpha_{t-1}} x_{t-2} + \sqrt{1 - \alpha_t \alpha_{t-1}} \epsilon_{\text{t-2}}^{\prime}, \quad &(\epsilon_{\text{t-2}}^{\prime} \sim \mathcal{N}(0, I)) \\\\ &= \sqrt{\alpha_t \alpha_{t-1} \alpha_{t-2}} x_{t-3} + \sqrt{1 - \alpha_t \alpha_{t-1} \alpha_{t-2}} \epsilon_{\text{t-3}}^{\prime}, \quad &(\epsilon_{\text{t-3}}^{\prime} \sim \mathcal{N}(0, I)) \\\\ &= \cdots \\\\ &= \sqrt{\bar{\alpha}_t} x_0 + \sqrt{1 - \bar{\alpha}_t} \epsilon'_0, \quad &(\epsilon'_0 \sim \mathcal{N}(0, I)) \end{aligned} $$ $ \begin{aligned} \text{따라서,} \quad q(x_t \mid x_0) = \mathcal{N}(x_t; \sqrt{\bar{\alpha}_t} x_0, (1 - \bar{\alpha}_t) I)이다. \end{aligned} $

  1. 결론적으로 diffusion process는 $x_0$을 조건부로 latent variables ($x_\text{1:T}$)를 생성해내는 과정이다.

Reverse Process

  1. 다음은 Reverse Process에 대한 설명이다.
  • Reverse process는 diffusion process의 역과정으로, gaussian noise를 제거해가며 특정한 패턴을 만들어가는 과정

  1. Reverse Process는 diffusion process에서 만든 $x_T$(noise)를 다시 복원해야 하는데, 이때 $q(x_\text{t-1} \mid x_t)$를 바로 구할 수 없다.
  • 그래서 모델 학습이 필요한 이유이다.

  1. 따라서 $q$를 approximation하는 $p_\theta$ 를 $p_\theta(x_\text{t-1} | x_t) \sim q(x_\text{t-1} | x_t) $ 와같이 정의한다. 이를 식으로 표현하면 아래와 같다.

$$ p_\theta(x_\text{0:T}) := p(x_T) \prod_{t=1}^{T} p_\theta(x_\text{t-1} \mid x_t), \quad p_\theta(x_\text{t-1} \mid x_t) := \mathcal{N}(x_\text{t-1}; \mu_\theta(x_t, t), \Sigma_\theta(x_t, t)) $$

  1. 위 식의 $\mu_\theta(x_t, t)$ 와 $\Sigma_\theta$ 는 학습되어야 할 parameter들이고, 위 식의 시작 지점인 $x_T$의 분포는 $p(x_T) = \mathcal{N}(x_T;,0,I)$ 로 표준정규분포로 정의한다.

Object Function (Loss)

  1. 이젠 $p_\theta$를 추정하기 위하여 model의 학습 방법을 알아보겠다.

  1. Model의 목적은 실제 data의 분포인 $p_\theta(x_0)$을 찾아내는 것을 목적으로 하기 때문에 결국 이의 likelihood를 최대화 하는 것이 목적이다.
  • $p_\theta(x_0)$ 를 직접 계산하기엔 어렵기 때문에, 변분 추론(variational inference)을 사용하여 diffusion process를 이용한 ELBO(Evidence Lower Bound)를 유도한다.

$$ \mathbb{E} \left[ - \log p_\theta(x_0) \right] \leq \mathbb{E_q} \left[ - \log \frac{p_\theta(x_\text{0:T})} {q(x_\text{1:T} \mid x_0)} \right] = \mathbb{E_q} \left[ - \log p(x_T) - \sum_{t \geq 1} \log \frac{p_\theta(x_\text{t-1} \mid x_t)}{q(x_t \mid x_\text{t-1})} \right] =: L $$

자세한 증명 보기 $$ \begin{aligned} -\log p_\theta(x_0) &\leq -\log p_\theta(x_0) + D_\text{KL} \left( q(x_\text{1:T} | x_0) || p_\theta(x_\text{1:T} | x_0) \right) \\\\ &= -\log p_\theta(x_0) + \mathbb{E_{x_\text{1:T} \sim q(x_\text{1:T} | x_0)}} \left[ \log \frac{q(x_\text{1:T} | x_0)}{p_\theta(x_\text{0:T}) / p_\theta(x_0)} \right] \text{($\log$의 분모가 $x_\text{0:T}$ 인 이유는 아직 모르겠다.)} \\\\ &= -\log p_\theta(x_0) + \mathbb{E_{x_\text{1:T} \sim q(x_\text{1:T} | x_0)}} \left[ \log \frac{q(x_\text{1:T} | x_0)}{p_\theta(x_\text{0:T})} + \log p_\theta(x_0) \right] \\\\ &= \mathbb{E_q} \left[ \log \frac{q(x_\text{1:T} | x_0)}{p_\theta(x_\text{0:T})} \right] \\\\ &= \mathbb{E_q} \left[ -\log \frac{p_\theta(x_\text{0:T})}{q(x_\text{1:T} | x_0)} \right] \\\\ \end{aligned} $$
  • 2번째 식에서 $\log$ 의 분모식이 $x_\text{0:T}$ 인 이유를 추론해보자면 ELBO는 상한을 설정하는 것이다.
  • 따라서, 전체 확률 분포 $p_\theta(x_\text{0:T})$를 기준으로 변분 추론을 전개하고 있다고 생각이 든다.

  1. 그렇기 때문에 이를 식으로 나타내면 위의 식과 같다.

  1. 위의 식을 좀 더 쉽게 계산하기 위해 아래와 같은 Gaussian 분포 간의 KL divergence 형태로 식을 변형한다.

$$ \mathbb{E_q} \Bigg[ D_\text{KL} \left( q(x_T | x_0) || p(x_T) \right) + \sum_{t > 1} D_\text{KL} \left( q(x_\text{t-1} | x_t, x_0) || p_\theta(x_\text{t-1} | x_t) \right)- \log p_\theta(x_0 | x_1)\Bigg] $$

  • 왼쪽 항 부터 $L_T, L_\text{T-1}, L_0$ 이다.
자세한 증명 보기

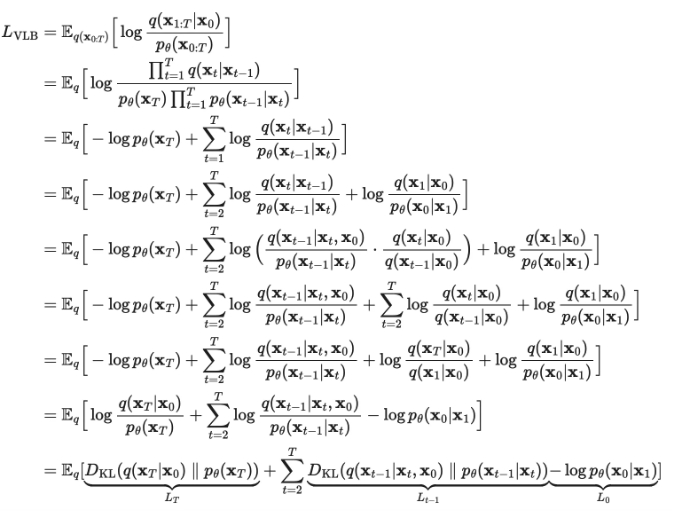
  1. 위 식에서 각각의 term이 가지는 의미를 하나씩 살펴보면 다음과 같다.

  1. $L_T$(regularization) : $p$ (diffusion process)가 generate하는 $noise(x_T)$와 $q$가 $x_0$ 라는 데이터가 주어졌을 때 generate하는 $noise(x_T)$ 간의 분포 차이이다.

  1. $L_\text{T-1}$(denoising process) : $p$와 $q$의 reverse / forward process의 분포 차이이다. 이들을 최대한 비슷한 방향으로 학습한다.
  • 즉, $p$라는 조건부 gaussian 분포는 $q$라는 조건부 gaussian 분포를 approximation하도록 학습이 된다는 것을 알 수 있다.

  1. $L_0$(reconstruction) : latent $x_1$으로부터 data $x_0$를 추정하는 likelihood. 이를 maximize하는 방향으로 학습한다.
  • negative log likelihood 이므로 maximize하는 방향으로 학습이 된다.

  1. 각 term들의 자세한 내용은 Diffusion models and denoising autoencoders에서 다루겠다.

  1. 마지막으로 $q(x_\text{t-1} | x_t)$ 는 계산하기 어렵지만 $q(x_\text{t-1} | x_t,x_0)$는 쉽게 계산을 할 수 있게 된다. 해당 식과 자세한 증명은 아래에 있다.
  • $x_t$에서 $x_\text{t-1}$을 바로 구하는 것은 어렵지만 $x_0$을 조건으로 주면 쉽게 구할 수 있다.

$$ q(x_{t-1} | x_t, x_0) = \mathcal{N} \left( x_{t-1} ; \tilde{\mu}_t(x_t, x_0), \tilde{\beta}_t I \right), $$

$$\text{where} \quad \tilde{\mu_t} (x_t, x_0) := \frac{\sqrt{\bar{\alpha_\text{t-1}}} \beta_t}{1 - \bar{\alpha_t}} x_0 + \frac{\sqrt{\alpha_t} (1 - \bar{\alpha_{t-1}})}{1 - \bar{\alpha_t}} x_t\quad \text{and} \quad\tilde{\beta_t} := \frac{1 - \bar{\alpha_{t-1}}}{1 - \bar{\alpha_t}} \beta_t $$

자세한 증명 보기

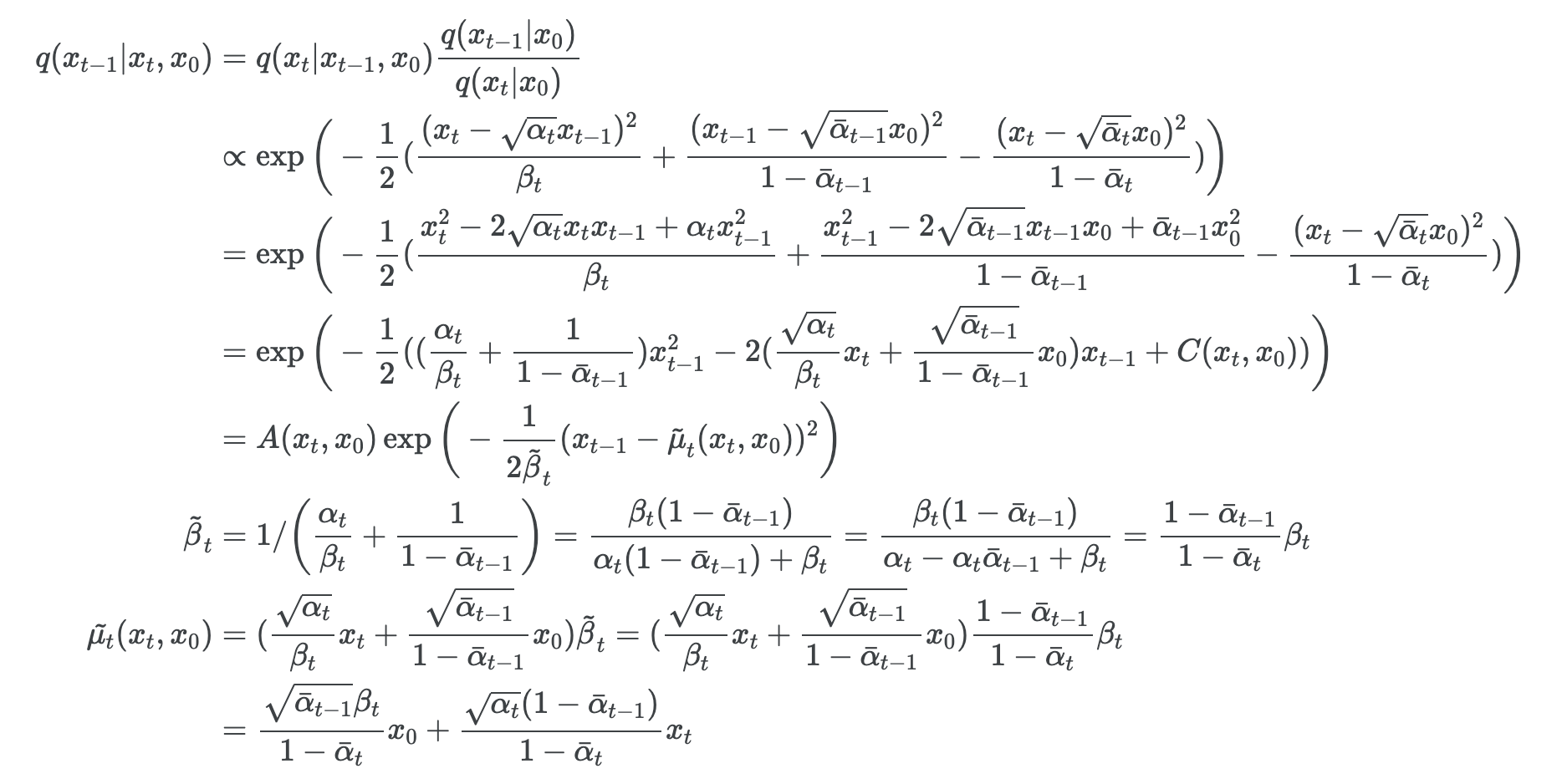
Diffusion models and denoising autoencoders

  1. Diffusion model의 설계 시 foward process, $\beta_t$, model 구조 등의 선택에 따라 달라지는 복잡한 모델이다.

  1. 해당 챕터에서는 이를 단순화 하기 위한 방법을 설명을 한다.

Forward process and $L_T$

  1. 16번에서 설명했듯이 $\beta_t$를 learnable parameter로 두는 것이 아니라, constant로 고정한다.

  1. 따라서, 28번에서 설명한 최종 Loss term 중 $L_T$의 식에서 posterior $q$는 학습이 되는 파라미터가 존재하지 않는다.
  • 그래서 학습 중에 무시할 수 있게 된다.

Reverse process and $L_\text{1:T −1}$

  1. 23번의 reverse process의 식 $p_\theta(x_\text{t-1} \mid x_t) := \mathcal{N}(x_\text{t-1}; \mu_\theta(x_t, t), \Sigma_\theta(x_t, t))$ 에서 $\mu_\theta(x_t, t)$ 와 $\Sigma_\theta$ 는 학습되어야 할 parameter들이라고 설명한 바가 있다.
  • $\mu_\theta(x_t, t)$는 평균, 즉 모델이 예측하는 깨끗한 데이터 $x_\text{t-1}$​ 의 값
  • $\Sigma_\theta$ 는 분산, 즉 모델이 예측한 값의 불확실성

  1. 주입된 noise 크기인 $\beta_t$를 이미 알고있기 때문에 이를 활용하여 분산($\Sigma_\theta$)을 대신 한다. 학습 대상이었던 분산을 각 시점에서 누적된 노이즈 크기로 상수화 하게 된다.

  • 논문에서는 $\sigma^2 = \beta_t$ 와 $\sigma^2 = \tilde\beta_t$ 의 실험 결과가 비슷하다고 설명한다.

    두개의 차이점
    • $\sigma^2 = \beta_t$ : 단순히 정방향 과정에서 사용된 $\beta_t$ 값을 그대로 reverse process에서 사용하겠다는 방법이다.
    • $\sigma^2 = \tilde\beta_t$ : 정방향 과정에서 누적된 노이즈도 반영하겠다는 방법이다.
    • Diffusion model은 다중 스텝을 거치므로 개별 스텝의 미세한 차이는 결과에 큰 영향을 미치지 못하기 때문에 결과가 비슷하다.
      • 즉, 스텝별 미세한 분산 차이가 최종적으로 누적될 때 무시할 수 있을 정도로 작을 수 있다.

  1. 따라서 $\Sigma_\theta(x_t, t) = \sigma_t^2 = \tilde\beta_t = t$시점까지의 누적된 $noise$ 가 된다.
  • $\tilde{\beta_t} := \frac{1 - \bar{\alpha_{t-1}}}{1 - \bar{\alpha_t}} \beta_t$
  • 평균 $\mu_\theta(x_t, t)$ 만이 학습되어야 할 parameter이다.

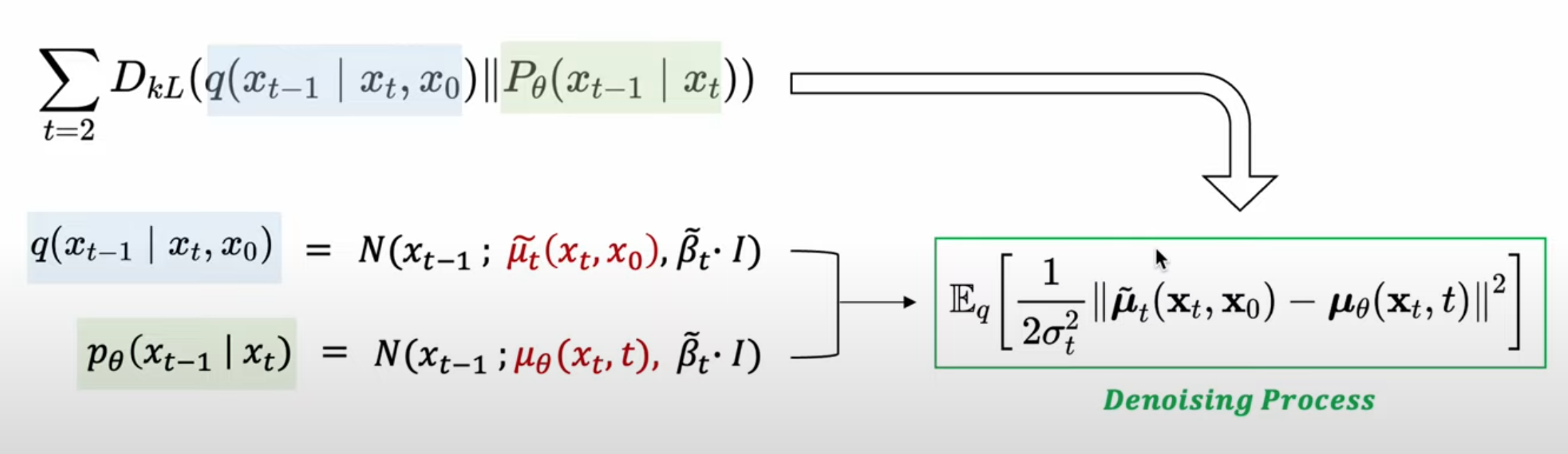
  1. 그렇기 때문에 위 그림 처럼 denoising process loss term($L_\text{t-1}$)의 목적식을 재구성 할 수 있게 된다.
  • 평균만이 학습대상이므로, 각각의 mean function간의 차이로 재정의 할 수 있게 된다.

$$ x_t(x_0, \epsilon) = \sqrt{\bar{\alpha}_t} x_0 + \sqrt{1 - \bar{\alpha}_t} \epsilon, \quad \epsilon \sim \mathcal{N}(0, I) $$

  1. 19번의 식을 reparametrization trick을 사용하여 표현하면 위 식이 된다. 이 식을 위 그림에 대입 하면 아래의 수식으로 정리가 된다.

$$\mathbb{E_{x_0, \epsilon}} \Bigg[ \frac{1}{2 \sigma_t^2} \Big|\Big| \frac{1}{\sqrt{\alpha_t}} \Big( x_t(x_0, \epsilon) - \frac{\beta_t}{\sqrt{1 - \bar{\alpha}_t}} \epsilon \Big) - \mu _ {\theta} \Big( x_t(x_0, \epsilon), t \Big) \Big|\Big|^2 \Bigg] $$

  1. 위 수식을 보면 $\mu _ {\theta} (x_t, t)$ 는 주어진 $t$시점에 $\frac{1}{\sqrt{\alpha_t}} ( x_t - \frac{\beta_t}{\sqrt{1 - \bar{\alpha}_t}} \epsilon)$의 식을 예측을 해야되는 것을 알 수 있다.

  1. $x_t$(input) 와 $t$는 주어진다. 따라서 남은 예측 대상(변수)은 noise($\epsilon$) 뿐이다.
  • $\epsilon$을 제외한 나머지 변수는 구할 수 있는 값들이다.

  1. 또한 이는 $p$분포의 평균($\mu _ {\theta}$)이 $q$분포의 평균($\frac{1}{\sqrt{\alpha_t}}$)을 예측하는 것으로 생각할 수 있다.

  1. 다르게 생각한다면, p분포를 q분포를 기반으로 parameterization해서 얻을 수 있다면 더욱 간단할 것이다. 아래는 그렇게 변형한 수식이다.
  • 6번에 대한 설명
    • 이 부분이 denoising matching의 핵심이다.

$$ \mu_{\theta}(x_t, t) = \tilde{\mu_t} \left( x_t, \frac{1}{\sqrt{\bar{\alpha_t}}} \left( x_t - \sqrt{1 - \bar{\alpha_t}} \epsilon _ {\theta}(x_t) \right) \right) = \frac{1}{\sqrt{\alpha_t}} \left( x_t - \frac{\beta_t}{\sqrt{1 - \bar{\alpha_t}}} \epsilon_{\theta}(x_t, t) \right) $$

  • 위 식을 이용하면 $x_\text{t-1}$을 바로 계산하는 것이 아니라 noise($\epsilon$)을 예측하여 $x_t$에서 빼는 방식을 취한다.
  1. 최종적으로 44번 위 수식과 위 수식을 조합한다면 DDPM의 최종 Loss Term이 도출 된다.
  • 본 논문에선 계수 term을 제외한 식의 Loss를 사용한다.
  • Loss가 굉장히 간단한 식으로 정의된다.
    • Noise를 예측하는 방식의 훈련이 진행되도록 설계가 되었다.

$$ \text{Loss} _ {\text{DDPM}} = \mathbb{E_{x_0, \epsilon}} \Bigg[ \frac{\beta_t^2}{2 \sigma_t^2 \alpha_t (1 - \bar{\alpha}_t)} \Bigg| \epsilon - \epsilon _ {\theta} \big( \sqrt{\bar{\alpha}_t} x_0 + \sqrt{1 - \bar{\alpha}_t} \epsilon, t \big) \Bigg|^2 \Bigg] $$

$$ = \mathbb{E_{x_0, \epsilon}} \Bigg[ \Big( \epsilon - \epsilon _ {\theta} \big( \sqrt{\bar{\alpha}_t} + \sqrt{1 - \bar{\alpha}_t} \epsilon, t \big) \Big)^2 \Bigg] $$

Experiment

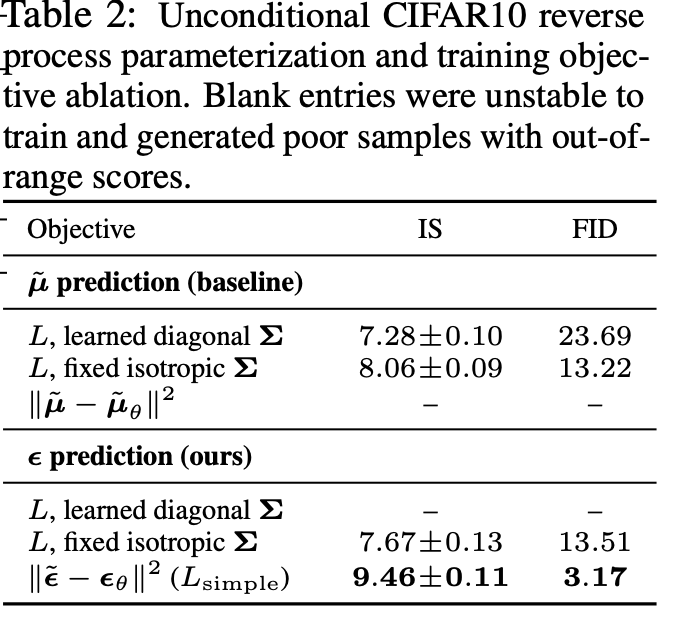
  1. 평균을 예측하는 것이 아니라, noise를 예측하는게 결과가 더 좋게 나온다.

  1. 또한 마지막 Loss에서 계수 term을 제거한 것이 더욱 결과가 좋게 나온다고 나온다.

  1. 왜냐하면 계수 term에서 $t$가 증가할 수록 분모가 더 빠르게 증가하기 때문에, $t$가 증가할수록 그 값이 작아지는 경향을 갖게 된다.
  • 계수 term은 Loss에서 가중치 역할을 하게 된다.
  • 항이 크면 손실이 더 강조, 작으면 덜 강조가 된다.

  1. 따라서 계수 term이 있으면 $T$(large t)시점에선 줄어들기 때문에 결론적으로 Loss의 영향이 줄어들게 된다.

  1. 그렇기 때문에 계수 term을 제외한 학습의 결과가 더 좋게 나온다.
  • $T$(large t)의 Loss 비중을 높여, 모델이 noise가 심한 이미지(large t시점의 상태)의 denoising에 집중하도록 유도가 된다.

Implement

  1. 코드에 대한 구현은 여기에 해두었다.

Reference

Updated on 2025-01-15
 논문 리뷰, computer vision, Diffusion, DDPM, Implement
Back | Home