[Paper Review]Denoising Diffusion Implicit Models(DDIM)
개요
DDPM이후DDPM의 샘플링 속도를 개선하여 보다 빠른 생성이 가능한DDIM에 대하여 논문 리뷰 할 것이다.
Introduction
Deep generative model은 여러 분야에서 높은 품질의 샘플을 생성할 능력을 보여준다.
GAN은 다른 어떤 생성 모델보다 더 높은 품질의 샘플을 생성 할 수 있다.
- 그러나
GAN은 매우 특정한 최적화 기법과 네트워크 구조를 선택해야 돼서, data 분포가 여러 모드를 충분히 학습하지 못하는 현상이 발견된다.
- 따라서 최근 연구에선
DDPM같은 생성 모델이GAN과 유사한 성능을 생성할 수 있다.
DDPM과 같은 모델들은adversarial training을 하지 않고,gaussian noise가 다양한 정도로 추가된 샘플을 복원하도록denoising autoencoder를 훈련하는 방식으로 동작한다.
- 샘플링 과정은
Markov chain방식을 따르며, 처음에는화이트 노이즈에서 시작하여 점점denoising하여 이미지를 복원하는 방식으로 진행된다.
- 이는
Langevin dynamics와forward diffusion과정을 역전시키는 두 가지 방식으로 구현이 된다.
DDPM과 같은 모델들은 샘플을 생성하는데많은 반복이 필요하다는 것이 문제점이다. 따라서GAN에 비하여 속도가 매우 느리다.
- 또한 이미지의 크기가 커질수록 더욱 심각해진다.
- 따라서 본 논문은
DDPM과GAN의 효율성 차이를 줄이기 위해DDIMs을 제안한다.
DDIM은암시적 확률 모델(implicit probabilistic models)(Mohamed & Lakshminarayanan, 2016)과 밀접한 관련이 있다.
암시적 확률 모델은DDPM과 동일한 목적 함수로 훈련된다는 점에서 유사하다.
- 본 논문에서는 기존
DDPM의Markov Chain확산 과정을Non-Markovian확산 과정으로 일반화 한다.
Non-Markov를 사용하면짧은 마르코프 체인을 구성할 수 있게 된다.- 이는, 샘플링 속도를 획기적으로 줄일 수 있게 된다.
- 따라서
동일한 신경망(목적 함수)를 사용하면서도,Markov가 아닌 다양한 확산 과정을 선택함으로써 더욱 넓은 범위의 생성 모델을 자유롭게 선택할 수 있다.
-
또한,
DDIM은DDPM과 비교하여 세 가지의 장점을 지닌다.- 샘플링 속도를 더욱 가속화 해도
DDPM과 비교하여 더 뛰어난 샘플 품질을 제공한다. DDIM에 일관성 속성이 있기 때문에초기 latent variable에서 출발하여높은 수준의 특징을 공유하게 된다.초기 latent variable을 조작하여 의미적으로 유의미한 이미지 보간을 수행할 수 있다.
- 샘플링 속도를 더욱 가속화 해도
Background
- 해당 부분에서는
DDPM의 전반적인 내용에 대해서 설명을 한다. 이는 이전의 글에 더 자세히 나와 있다.
DDPM의 샘플링 속도가 너무 느려 이를 해결하기 위해DDIM이 등장하여 속도를 개선한다.
Variational Inference For Non-Markovian Forward Processes
- 생성 모델은
inference process의역(reverse)을 추정하기 때문에, 많은 반복을 줄이기 위해inference process에 대한 새로운 접근이 필요하다.
DDPM의 핵심적인 관찰은DDPM의목적함수가 오직marginal probability distribution(주변 확률 분포)$q(x_t \mid x_0)$에만 의존하고joint distribution(공동 확률 분포)$q(x_\text{1:T}\mid x_0)$엔 직접적으로 의존하지 않는다는 점이다.
- 즉, 동일한
주변 확률 분포를 가지면서 다양한공동 확률 분포가 존재하기 때문에,Markovian특성을 갖지 않는 대체적인 생성 과정을 설계할 수 있다.
Non-Markovian추론 과정을 사용하더라도DDPM과동일한 대리 목적 함수를 유지할 수 있다.
Non-Markovian Forward Porcesses
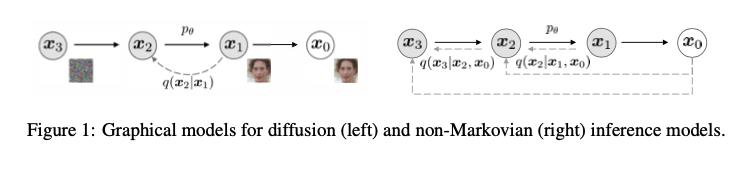
- 따라서
주변 확률 분포인 $q_\sigma(x_T|x_0)$ 는 $q_\sigma(x_T|x_0) = \mathcal{N}(\sqrt{\alpha_T}x_0, (1 - \alpha_T)I)$ 는DDPM과DDIM둘 다 만족한다.
- 하지만 공동 확률 분포인 $q_\sigma(x_\text{1:T}|x_0)$에 대해서는
DDPM과DDIM이 아래와 같이 다르게 표현되고 있다.
$$ \begin{aligned} DDPM &: q(x_\text{1:T} | x_0) := \prod_\text{t=1}^T q(x_t | x_\text{t-1}) \\ DDIM &: q(x_\text{1:T} | x_0) := q_\sigma(x_T|x_0) \prod_\text{t=2}^T q_\sigma(x_\text{t-1} | x_t,x_0) \end{aligned} $$
DDIM의 공동 확률 분포 증명 확인
- 각 시간 단계 $x_t$가 단순히 $x_\text{t-1}$에만 의존하는 것이 아니라, $x_0$에 대한 직접적인 정보도 포함하도록 식을 변형 하려고 한다. $$ \begin{aligned} q_{\sigma}(x_{1:T} | x_0) &:= q(x_1 | x_0) q(x_2 | x_1, x_0) q(x_3 | x_2, x_0) \dots q(x_T | x_{T-1}, x_0) \\ &:= \cancel{q(x_1 | x_0)} \frac{q(x_1 | x_2, x_0) \cancel{q(x_2 | x_0)}} {\cancel{q(x_1 | x_0)}} \frac{q(x_2 | x_3, x_0) \cancel{q(x_3 | x_0)}}{\cancel{q(x_2 | x_0)}} \dots \frac{q(x_{T-1} | x_T, x_0) q(x_T | x_0)}{\cancel{q(x_{T-1} | x_0)}} \\ &(\therefore q(x_T | x_{T-1}, x_0) = \frac{q(x_{T-1} | x_T, x_0) q(x_T | x_0)}{q(x_{T-1} | x_0)} \text{From Bayes’ rule})\\ &:= q_\sigma(x_T|x_0) \prod_\text{t=2}^T q_\sigma(x_\text{t-1} | x_t,x_0) \end{aligned} $$
- 따라서
DDPM은Markovian의 특성을 가지고 있지만,DDIM은Non-Markovian의 특징을 가지고 있다는 것을 알 수 있다.
q의 분포가 $x_t$가 $x_\text{t-1}$와 $x_0$에 의존하기 때문에 더이상 markovian이 아니게 되는 것이다.Forward Process를위 식과 같이 정의하는 것은 직접적인 성능 향상을 주는 것은 아니다.Reverse Process에서 결정론적 샘플링과 빠른 샘플링을 가능하게 하려면Forward Process를 이렇게Non-Markovian을 사용하여 정의가 되어야 하기 때문이다.
DDIM에서위 식을 만족하면mean function은아래의 식을 만족하게 된다.
$$q_{\sigma}(x_{t-1} | x_t, x_0) = \mathcal{N} \left( \sqrt{\alpha_{t-1}} x_0 + \sqrt{1 - \alpha_{t-1} - \sigma_t^2} \cdot \frac{x_t - \sqrt{\alpha_t} x_0}{\sqrt{1 - \alpha_t}}, \sigma_t^2 I \right)$$
증명 확인
$$ \begin{aligned} x_{t-1} &= \sqrt{\bar{\alpha_{t-1}}} x_0 + \sqrt{1 - \bar{\alpha_{t-1}}} \mathbf{z_{t-1}} \\ &= \sqrt{\bar{\alpha_{t-1}}} x_0 + \sqrt{1 - \bar{\alpha_{t-1}} - \sigma_t^2} \mathbf{z_t} + \sigma_t \mathbf{z} \quad (\therefore \text{reparameterization trick})\\ &= \sqrt{\bar{\alpha_{t-1}}} x_0 + \sqrt{1 - \bar{\alpha_{t-1}} - \sigma_t^2} \frac{x_t - \sqrt{\bar{\alpha_t}} x_0}{\sqrt{1 - \bar{\alpha_t}}} + \sigma_t \mathbf{z} \quad (\therefore x_{t} = \sqrt{\bar{\alpha_{t}}} x_0 + \sqrt{1 - \bar{\alpha_{t}}} \epsilon)\\ q_{\sigma}(x_{t-1} | x_t, x_0) &= \mathcal{N} \left( x_{t-1}; \sqrt{\bar{\alpha_{t-1}}} x_0 + \sqrt{1 - \bar{\alpha_{t-1}} - \sigma_t^2} \frac{x_t - \sqrt{\bar{\alpha_t}} x_0}{\sqrt{1 - \bar{\alpha_t}}}, \sigma_t^2 I \right) \end{aligned} $$
DDPM에서 $q$에 대해서 평균과 분산을 구해서 정의를 내렸지만,DDIM에서는바로 위 식처럼 가우시안 식으로 정의를 내릴 수 있다.
- $DDPM : q(x_{t-1} | x_t, x_0) = \mathcal{N} \left( x_{t-1} ; \tilde{\mu}_t(x_t, x_0), \tilde{\beta}_t I \right)$
- $\sigma$의 값은
forward process가 얼마나stochastic한지 컨트롤 하며, 이 값이 0에 가까워질수록 $x_\text{t-1}$값이 fix 되며deterministic해진다.
Generative Process and Unified Variational Inference Objective
- 다음으로 학습 가능한 생성 과정인 $p_\theta(x_\text{0:T})$를 정의한다. 이때 $ p_{\theta}^{(t)}(x_{t-1} | x_t)$는 $ q_{\sigma}(x_{t-1} | x_t, x_0)$ (
reverse conditional distribution)에 대해 알고있는 정보를 활용한다.
reverse conditional distribution: noisy한 $ x_t$ 가 있을 때, $ x_0$를 이용해 $ x_{t-1}$를 샘플링
- 따라서 $p_\theta(x_\text{0:T})$ 가 수행되기 위하여 노이즈 관측 값인 $ x_t$에 대해 우리는 가장 먼저 대응하는 $x_0$를 예측하고, $ q_{\sigma}(x_{t-1} | x_t, x_0)$을 통하여 샘플 $ x_{t-1}$을 얻는다.
- 다음은 위 과정을 조금 더 자세하게 설명한 부분이다.
- $ x_0 \sim q(x_0)$와 $ \epsilon_t \sim \mathcal{N}(0, I)$에 대해 $ x_t = \sqrt{\alpha_t} x_0 + \sqrt{1 - \alpha_t} \epsilon$을 수행하여 $ x_t$를 얻어낼 수 있다.
- 모델 $ \epsilon_{\theta}^{(t)}(x_t)$는 $ x_0$에 대한 정보 없이 $ x_t$로부터 $ \epsilon_t$를 예측한다.
위 식을 $ x_0$에 대해 다시 표현하면 우리는 $x_t$에 대한 $ x_0$의 예측 값인 denoised observation 을 알 수 있다.
$$f_{\theta}^{(t)}(x_t) := \frac{x_t - \sqrt{1 - \alpha_t} \cdot \epsilon_{\theta}^{(t)}(x_t)}{\sqrt{\alpha_t}}$$
- 내가 이해한 대로 정리하자면, 기존
DDPM에서 사용되었던Forward Process$(x_t = \sqrt{\alpha_t} x_0 + \sqrt{1 - \alpha_t} \epsilon )$ 의 식을 $x_0$ 식으로 변경하여 생성 과정$(p_\theta(x_\text{0:T}))$ 시 $f_{\theta}^{(t)}(x_t) := x_0$를 샘플링하여(denoised observation= 노이즈가 제거된 관측값) 사용(추정)하겠다는 의미이다.
DDIM에서 기존DDPM에서의Forward Process에서의 과정은 변함이 없다.모델$(\epsilon_{\theta}^{(t)}(x_t))$의 역할(노이즈 예측)도 동일히다.
- 또한
fixed prior인 $ p_{\theta}(x_T) = \mathcal{N}(0, I)$를 통해 generative process를 아래와 같이 정의할 수 있다. $$p_{\theta}^{t}(x_{t-1} | x_t) = \begin{cases} \mathcal{N}(f_\theta^{1}(x_1), \sigma_1^2 I) & \text{if } t = 1 \\ q_\sigma(x_{t-1} | x_t, f_{\theta}^{t}(x_t)) & \text{otherwise} \end{cases} $$
- 항상
generative process를 보장하기 위해 $t = 1$ 일 때gaussian noise$( \sigma_1^2 I )$를 추가해준다. - $f_{\theta}^{t}$가 $x_0$을 대체했다.
- 아래는
generative process를 최적화 시키기 위해 이용되는variational lower bound의 형태이다.

- 해당 논문에서는 $\sigma$를 어떻게 선택하느냐에 따라서 다른 목적 함수가 되는데, 만약, $\sigma$가 0보다 크다면
DDPM의ELBO와 같은 형태가 되고, 0이면DDIM의 목적 함수이다.
- 즉
DDIM에서는non-markovian을 위해서 $\sigma$를 0으로 설정한다.
- 해당 정보를 사용하여 본 논문은
Theorem 1을 정의하였다.
$$\textbf{Theorem 1. \quad} \textit{For all } \sigma > 0, \textit{ there exists } \gamma \in \mathbb{R_\geq^T} \textit{ and } C \in \mathbb{R}, \textit{ such that } J_\sigma = L_\gamma + C$$
- $\gamma = 1$이라면,
objective function은DDPM의variational lower bound와 같다.
- $L_1 = J_\sigma$
- $J_\sigma$는 $L_\gamma$의 일종인데, 이는 $\gamma = 1$일 때
DDIM에서도 ($L_1$) 최적의 값을 가져서 최적의 학습이 가능하다는 뜻이다.
objective function의 $\gamma = 1$일때 최적의 값은DDPM에서 언급 된 내용이다.
Sampling From Generalized Generative Process
35번에서 말한대로 $\gamma = 1$ 일 때optimal을 구할 수 있으므로 $L_1$을objective function으로 두고 사용하는 경우를 살펴보자.
- 그럴 경우 $\sigma$를 어떻게 설정하느냐에 따라
forward process를markovian이나non-markovian으로 학습 시킬 수 있게 된다.
- 이때 $\sigma$ 의 값과는 상관 없이 학습해야하는
parameter는 $\theta$ 라는 점이다.모델($\theta$)이 학습하는 것은forward process의 형태와는 독립적이다.
- 결론적으로
markovian process로 학습시킨DDPM의 학습한 모델($\theta$)를DDIM의generative process에서 사용할 수 있게 된다는 것이다.
DDIM은새로운 학습 방식을 제안한 것이 아니라,새로운 샘플링 방법을 제안한 것이다.
Denoising Diffusion Implicit Model
21번 식($q_\sigma(x_\text{t-1}|x_t, x_0)$)과 $x_t = \sqrt{\alpha_t} x_0 + \sqrt{1 - \alpha_t} \epsilon$ 의 조합으로아래의 식을 유도할 수 있게 된다.
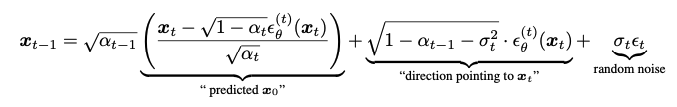
- 위 식은 $x_t$로부터 $x_\text{t-1}$을
sampling하는 과정을 뜻한다.
- $\sigma$의 값에 따라서
다른 process가 되며, 같은 $\epsilon_\theta$를 사용하기 때문에재학습은 불필요하다.
- $\sigma$가 0이 아니라면,
markovian에 따라서DDPM이 된다. $\sigma$가 0이라면,random noise가 0이 되기 때문에stochastic한확률적인 변수가 없어지기 때문에sampling process($x_T$ -> $x_0$)가 고정이 된다.
- $\sigma$가 0이 된다면,
forward process가 $x_\text{t-1}, x_0$에 대해deterministic해진다.- 이 부분이
Implicit Probabilistic Model이 되는 이유이다. - 명시적으로 확률 분포를 정의하지 않지만, 특정한 함수 형태로 확률적인 특성을 암시적으로 표현하는 모델을 의미한다.
- 이 부분이
reverse process진행 시 노이즈($x_T$)랑 이미지($x_0$)가1:1 매칭이 된다고 이해하면 될 것 같다.
Accelerated Generation Processes
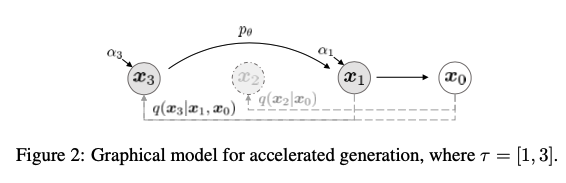
Forward process에서Tstep을 가지고 있다고 해도sampling과정에서 모든 스텝을 사용할 필요는 없다.
- 왜냐하면
forward process($q(x_t|x_0)$)이 고정되면,모델의 재학습을 할 필요 없이 샘플링 과정만 최적화 하면 된다.
일부 스텝만 선택해서 샘플링하면 비슷한 품질의 데이터를DDPM과 비교하여 훨씬 빠르게 생성 가능하다.

- 위 그림은
DDPM과DDIM의 차이점에 대한 내용을 나타낸 것이다. 그림을 보면 알 수 있듯이다른 과정은 같고,sampling 과정만 다른 것을 알 수 있다.
Experiments
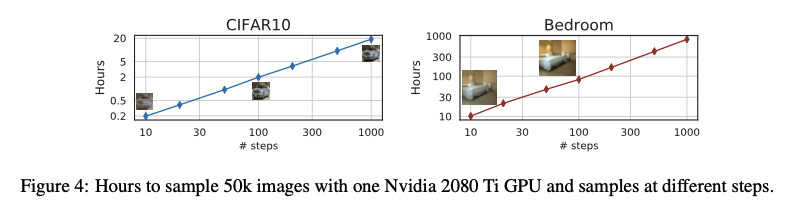
위 사진은 왼쪽이DDIM이고 오른쪽이DDPM의 성능을 비교한 사진이다.
DDPM이1000step정도 필요한 품질을 만드는 반면에DDIM은20step이면 생성할 수 있다.
DDIM이DDPM보다 50배 빠른 속도이다.

위 사진은 $x_T$는 이미지의 중요한high-level의 정보를 담고 있는latent encoding의 역할을 한다고 알 수 있다.
- 왜냐하면 같은 $x_T$에서 시작하고, 샘플링 경로가 다르더라도
고수준(high-level)특징을 가지는 이미지가 비슷하게 나오기 때문이다.
- 대부분
20step의 sample이1000step의 sample 이랑 유사해진다.

- 따라서
위 사진처럼semantic interpolation이 가능하다는 사실을 볼 수 있다.
- $x_T$사이에서 두 샘플 사이의
interpolation이 가능하다는 사실을 알 수 있다. (GAN에서도 할 수 있다.) 가운데 사진을 보면양쪽 이미지의 특성이 적절히 섞여있는 것을 알 수 있다.
Implement
- 코드에 대한 구현은 여기에 해두었다.