GoodYoung Dev Blog
Posts Tags Categories
GoodYoung Dev Blog

Contents

[CS236] 9. GANs - 1

GoodYoung included in DL Theory Lecture Deep Generative Models
   1180 words   6 minutes 

개요

  1. 이번 포스트에서는 CS236 강의의 8강을 설명한다.

  1. 우리는 지금까지 여러 생성 모델들을 배웠다. AutoRegreesive Model, Variational Autoencoder, Normalizing Flow. 이들은 모두 실제 데이터 분포 $p_\text{data}$ 에 제일 가까운 $p_\theta$ 를 찾으려고 했다. 가장 가까운 $\theta$ 를 찾기 위하여 Maximum log-likelihood(MLE)를 학습 목표로 삼았다.

  1. 그렇다면, 높은 log-likelihood가 무조건 좋은 품질의 생성을 의미할까? 아니다. likelihood가 낮더라도 sampling의 품질은 꽤 좋을 수 있다. 그래서 이번 lecture에서는 MLE에 기반하지 않는 다양한 종류의 훈련 목적 함수를 알아볼 것이다.

    • 높은 likelihood -> 나쁜 품질은 어떻게 하면 될까? 자세한 내용은 아래 toggle을 확인하면 된다.

      높은 likelihood -> 나쁜 품질 예시
      • 아래의 슬라이드를 보면, 99퍼센트의 noise를 추출하는 $p_\theta$ 이지만 높은 차원으로 갈 수록이 모델은 실제 $p_\text{data}$ 를 나타내는 예시를 볼 수 있다. 그렇게 되면 이 모델은 MLE는 매우 좋을 것이며, 샘플의 품질은 매우 나쁠 것이다.

    • 그렇다면 낮은 likelihood -> 좋은 품질은 어떻게 하면 될까? 그 방법은 모델을 overfitting을 하면 된다.


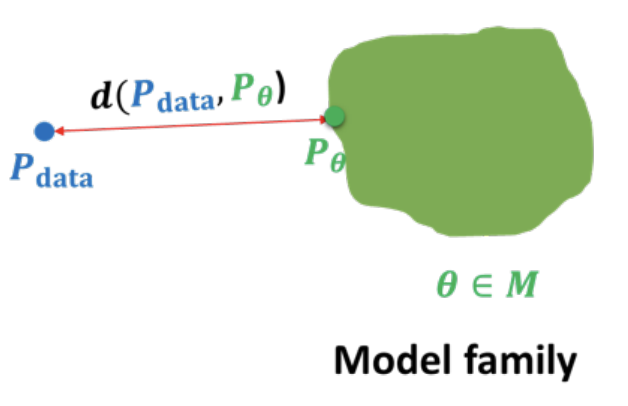
  1. 결론적으로 기존과 달리, 우리는 위 그림의 $d(p_\text{data}||p_\theta)$ 의 다른 대안을 알아볼 것이다.

Two-Sample Test

  1. 그렇다면 어떤 다른 방법이 있을까. 바로 두 개의 분포에서 생성한 결과를 가지고 그 생성한 결과가 서로 같다면 귀무가설(두 분포가 같다)을 받아드리고, 다르다면 기각하는 방식으로 MLE 없이 두 개의 분포 유사도를 측정할 수 있는 Two-Sample Test 방식이 있다.

    • 두 분포가 같음을 측정할 때 만약 두 분포의 평균만 사용한다면, 우리는 분포의 확률조차도 구할 필요가 없는 것이다.

    • 하지만, 통계적으로 고차원의 데이터에서 단지 평균만으로 측정한다면, 올바른 측정이 어렵다. 위와 같이 생각해야할 것들이 많기 때문이다. (단지, 평균만 같아도 두 분포가 같다고 할 수 없는 것(왼쪽 첫번째 그림) 처럼)


  1. 그렇다면 자동적으로 이 두 분포의 차이를 어떻게 알까? 방법은 분류기를 학습하는 것이다. (GAN에서 Discriminator 역할)
    • 본질적으로는, 우리가 딥러닝 분류기의 역할은 두(여러) 그룹의 샘플을 구별하고 구분할 수 있는 특징을 자동적으로 분류하는 것이다. 이를 Two-Sample Test에 적용시키겠다는 것이다.

Generative Adversarial Network (GAN)

Discriminator

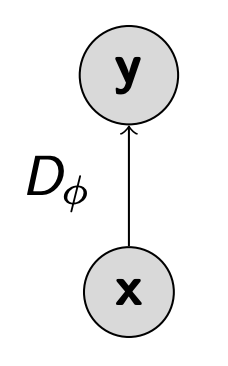
  1. 1일 때 real, 0일 때 fake 를 구별하는 2진 분류기가 있다고 하자. 그렇게 되면 우리가 사용할 통계량은 이 분류기의 loss일 것이다.(loss가 적으면 잘 구별한다는 것이고, 높으면 구별하기 어렵다는 것으로 해석할 수 있다.) 땨라서 이 분류기의 목표는 이 통계량을 최대화하거나 loss를 최소화하는 것이다.

$$ \begin{aligned} \max_{D_\phi} V(p_\theta, D_\phi) &= \mathbb{E_{x \sim p_{\text{data}}}}[\log D_\phi(x)] + \mathbb{E_{x \sim p_\theta}}[\log(1 - D_\phi(x))] \\ &\approx \sum_{x \in S_1} \log D_\phi(x) + \sum_{x \in S_2} \log(1 - D_\phi(x)) \end{aligned} $$

  • $p_\theta$: Fixed generative model
  • $p_\text{data}$: 데이터 셋
  • $D_\phi(x)$: Discriminator

  1. 이것은 고정된 생성 모델이 있을 때, 분류기의 목적 함수이다. 따라서 오직 분류기의 최적화 관점만 생각해야한다. 이 분류기는 $S1$에 대해서 1(real, 진짜로 인식)로 , $S2$에 대해서 0(fake, 가짜로 인식)로 잘 분류할 수 있게 학습하도록 한다. 이렇기 때문에 $D_\phi(x)$ 의 값은 샘플 $x$ 가 실제 데이터 분포에 속할 확률을 나타내는 것으로 해석할 수 있다. (데이터 분포와 유사하면 1, 아니면 0이기 때문이다.)

$$ D_\theta^*(x) = \frac{p_{\text{data}}(x)}{p_{\text{data}}(x) + p_\theta(x)} $$

  1. 그래서 위의 Discriminator 식을 최적화 한다면 위와 같은 식으로 표현할 수 있는데, 이는 x가 Discriminator에 들어왔을 때 전체 분포의 확률 중에 실제 데이터 분포일 확률을 나타낸다. 따라서, 만약 $p_\text{data} = p_\theta$ 라면($p_\text{data}$와 $p_\theta$의 분포가 같다면) 값은 1/2이 나올 것이다.

Generator

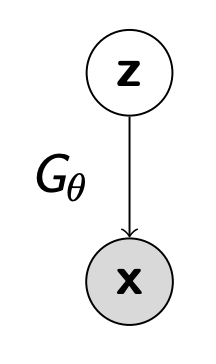
  1. 그렇다면 Discriminator를 속이기 위해 Generator ($p_\theta$)를 최적화 하는 방법을 정의해보자. Flow-model 처럼 유사하게 동작하지만, 역변환은 필요 없다. 쉬운 분포 p(z)에서 z를 뽑고 $G_\theta$ 에 넣어 x를 생성하는 것에 초점이 맞춰져 있다. 또한 여기서 나온 $p_\theta(x)$ 의 likelihood도 계산할 필요가 없다. Two-Sample Test에서 모델을 비교하며 학습하기 때문에 신경 쓸 필요 없다. (VAE 등의 다른 생성 모델은 $p(x,z)$를 학습하는데 초점이 맞춰져있다. )

  1. 이 모델을 사용하여 얻은 샘플 분포와 실제 데이터 분포가 동일하다는 귀무 가설을 뒷받침하는 통계를 최소화 하려고 한다.
    • Discriminator는 “두 분포가 다르다"는 증거(= test statistic)를 최대화하려고 한다.
    • Generator는 반대로 “두 분포가 다르지 않다"는 귀무가설을 성립시키고 싶기 때문에 그 증거를 최소화하려고 한다.

GAN Learning Objective

$$\min_G \max_D V(G, D) = \mathbb{E_{x \sim p_{\text{data}}}}[\log D(x)] + \mathbb{E_{x \sim p_G}}[\log(1 - D(x))]$$

  1. 위 식은 최종 목적 식이다. Discriminator는 최대화 하는 방향으로 학습을 하고, Generator는 최소화 하는 방향으로 학습을 하는 것을 볼 수 있다. 위에서 나온 최적의 Discriminator ($D^*_{\theta}(x)$) 를 위의 최종 목적 식에 대입해보면 다음과 같다.

$$ \begin{aligned} V(G, D_G^*(x)) &= \mathbb{E_{x \sim p_{\text{data}}}} \left[ \log \frac{p_{\text{data}}(x)}{p_{\text{data}}(x)+p_G(x)} \right] + \mathbb{E_{x \sim p_G}} \left[ \log \frac{p_G(x)}{p_{\text{data}}(x)+p_(x)} \right] \\ &= \mathbb{E_{x \sim p_{\text{data}}}} \left[ \log \frac{p_{\text{data}}(x)}{\frac{p_{\text{data}}(x)+p_G(x)}{2}} \right] + \mathbb{E_{x \sim p_G}} \left[ \log \frac{p_G(x)}{\frac{p_{\text{data}}(x)+p_G(x)}{2}} \right] - \log 4 \\ &= D_{\text{KL}}\left(p_{\text{data}} ;\middle|; \tfrac{p_{\text{data}} + p_G}{2}\right) + D_{\text{KL}}\left(p_G ;\middle|; \tfrac{p_{\text{data}} + p_G}{2}\right) - \log 4 \\ &= 2 D_{\text{JSD}}\left[p_{\text{data}} \parallel p_G\right] - \log 4 \end{aligned} $$


  1. 위의 긴 식을 차근 차근 풀어보겠다.

    • 2번째 줄에 Normalizing을 하기위하여 2로 나누고 $\log4$ 를 빼주었다.

      • $p_\text{data}, p_G$ 는 각각 독립적인 확률분포이므로 2로 나누어 정규화를 해주어야 한다.

    • 그렇게 되면 3번째 줄에 Expectation을 KL-Divergence 식으로 표현할 수 있다.

      • $D_{KL}(p \parallel q) = \sum_x p(x) \log \frac{p(x)}{q(x)}= \mathbb{E}_{x \sim p}\left[\log \frac{p(x)}{q(x)}\right]$

    • 마지막으로, 4번째 줄에, KL 식을 젠슨 - 섀넌 divergence(JSD)으로 다시 표현해줄 수 있게 된다.

    • 그럼 결국, GAN을 학습하는 것은 실제 데이터 분포와 모델의 샘플링 분포의 차이를 나타내는 JSD를 최적화 하는 문제와 동일해진다.

    젠슨-섀넌 Divergence란? $$D_{JSD}[p, q] = \frac{1}{2} \left( D_{KL}\!\left[p \,\bigg\|\, \tfrac{p+q}{2}\right] + D_{KL}\!\left[q \,\bigg\|\, \tfrac{p+q}{2}\right] \right)$$
    • 보통 데이터 분포와 모델 분포 사이의 차이를 젠슨 - 섀넌 divergence (대칭적 KL-divergence라고도 불린다.)
    • 이 식은 몇가지 특징이 있다.
      • 0보다 크다는 특징 (KL이 0보다 커서)
      • $D_{JSD}[p, q] = D_{JSD}[q, p]$, KL과는 다른 특징이다. (KL은 바뀌면 같지 않다.)
      • 분포가 동일할 때만 global optimum을 달성한다.
      • 따라서, 만약 두 분포가 같다면 $V(G^*, D_G^*(x)) = - \log4$ 일 것이다.

  1. 따라서, 우리는 기존과 달리 KL을 사용하지 않고, JSD를 사용하여 데이터 분포와 모델 분포 를 비교하는 방식을 사용한다. 이 점이 다른 생성 모델과 차별점이라고 할 수 있다. 또한 모델 손실을 평가하고 최적화하는데, $p_\theta$ 의 likelihood는 필요 없고 오직 샘플만 필요하다. 그렇기 때문에 GAN은 neural network $G_\theta$ 의 구조에 많은 유연성이 있다. 왜냐하면 우리는 그저 랜덤 노이즈를 넣고 샘플링만 하면 되는 $G_\theta$ 를 구하면 되기 때문이다. 그래서 single forward pass이기 때문에, 샘플링이 빠르다.

  1. 하지만 GAN은 문제점도 있다. 쉬워보이지만 현실에서 훈련되기 어렵고 까다롭다.(최소,최대 문제이기 때문에)

  1. GAN의 전체 훈련 흐름을 한번 살펴보자.

    • Step 1: m개의 Minibatch 훈련 데이터, ($x^{(1)}, x^{(2)}, \ldots, x^{(m)} \sim \mathcal{D}$)

    • Step 2: m개의 Noise 데이터, ($z^{(1)}, z^{(2)}, \ldots, z^{(m)} \sim p_z$)

    • Step 3: Discriminator 파라미터 $\phi$ 최적화 by stochastic gradient ascent $$\nabla_\phi V(G_\theta, D_\phi) = \frac{1}{m} \nabla_\phi \sum_{i=1}^m \Big[ \log D_\phi(x^{(i)}) + \log (1 - D_\phi(G_\theta(z^{(i)}))) \Big]$$

      • Real, Fake를 잘 분류하기 위한 훈련

    • Step 4: Generator 파라미터 $\theta$ 최적화 by stochastic gradient descent (첫번째 항은 필요 없음) $$\nabla_\theta V(G_\theta, D_\phi) = \frac{1}{m} \nabla_\theta \sum_{i=1}^m \log \big(1 - D_\phi(G_\theta(z^{(i)}))\big)$$

      • Discriminator를 속이기 위한 훈련

    • Step 5: Epoch마다 반복


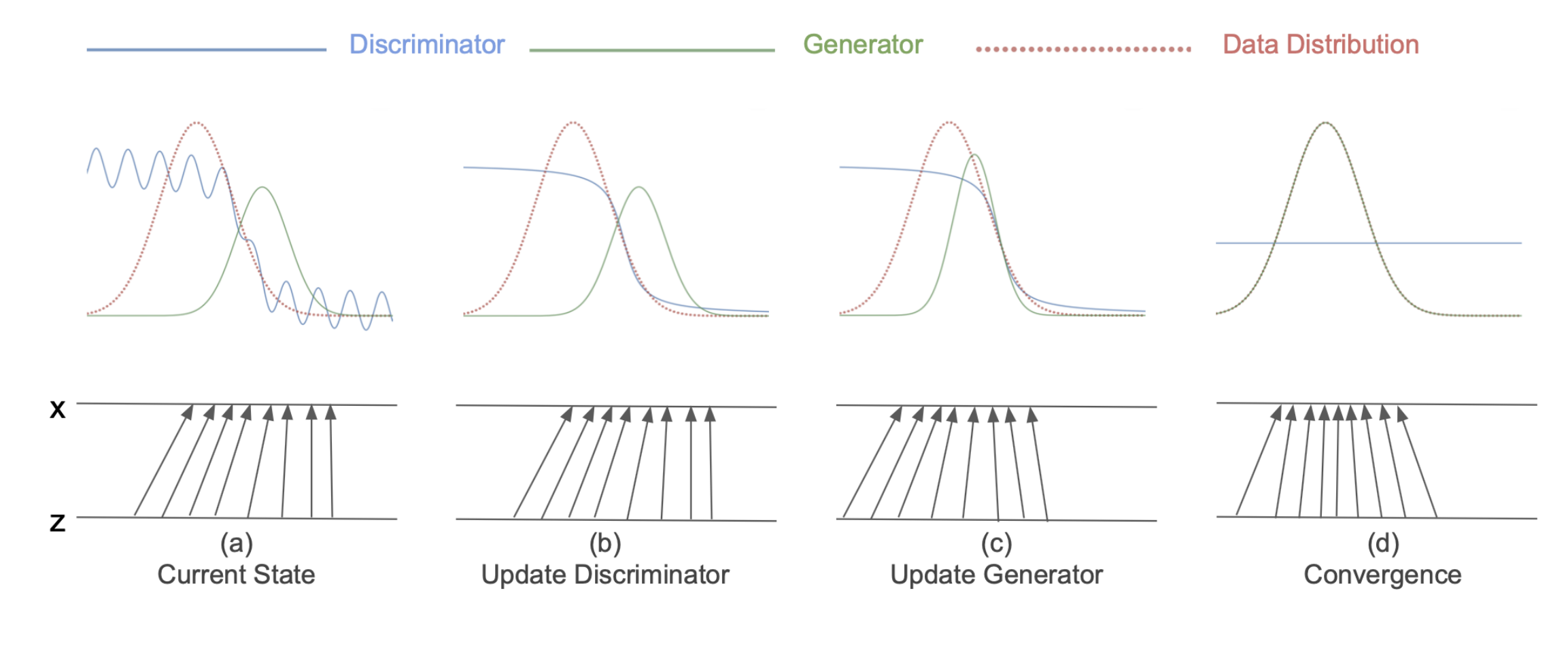
  1. 위 그림은 전체 훈련 흐름을 진행하면서 x,z 벡터가 업데이트 되는 방향을 시각적으로 나타낸다.
    • a->b 로 갈 떄 Discriminator를 최적화 되면서 왼쪽은 real일 확률이 높고, 오른쪽으로 갈수록 fake일 확률이 높다고 판단하며 학습이 된다.
    • b->c 로 갈때는 Generator가 최적화 되면서 점점 실제 분포(Data Distribution)으로 가까워지는 방향으로 옮겨지는 것을 확인할 수 있다.
    • c->d일 땐 Discriminator가 더이상 분류를 못하여 모든 데이터 포인트에서 1/2의 확률을 내뱉는 것을 볼 수 있다.

Challenges

  1. 이런 GAN은 특정 task에서 매우 성공적이었지만, 몇가지 단점도 발견되었다.

    • Unstable Optimization

      • 훈련 중 loss를 보면, 매끄럽게 수렴하는 것이 아니라 min,max 문제이기 때문에 훈련 loss 그래프가 진동하는 현상
      • 또한 어느 특정 시점에서 멈춰야하는지에 대한 기준(criteria)가 없다.
      • 따라서 GAN은 훈련이 매우 어렵다고 평가받는다.

    • Mode Collapse

      • 위 그림을 보면 생성한 샘플링의 벡터 위치를 2차원으로 나타낸 것인데, target의 모든 부분을 감싸는 것이 아니라 훈련을 진행할 때, 특정 부분만 보는 것을 확인할 수 있다.
        • 이는, Generator가 Discriminator를 속이는 방향에 따라 최적화가 진행되는 특성에 내재한 문제라고 볼 수 있다.
      • 따라서 샘플링 시 Generator가 Discriminator를 속이지만, 특정 부분만 반복적으로 생성하는 Mode Collapse 문제가 있다.

Reference

Updated on 2025-08-27
 GAN, CS236
Back | Home