[CS236] 8. Normalizing Flows - 2

개요

0. 이번 포스트에서는 CS236 강의의 8강을 설명한다.

1. 이전 포스트에서는 change of variable 공식을 사용하여 공식을 선형적인 예시부터, 비선형적인 예시까지 확장해보았다.

2. 이번 포스트에서는 공식을 가지고 더 나아가보겠다.

---

Normalizing Flow Models

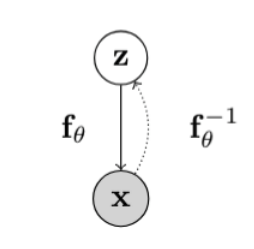
3. Flow Model은 위와 같이 결정적인 함수 식에 의하여 정해진다. 우리는 이에 대해서 배웠고 관련 공식도 배웠다. 이를 실제 neural network 모델에 사용하려면 어떻게 할까?

$$\mathbf{z_m} = f_\theta^{m} \circ \cdots \circ f_\theta^{1}(\mathbf{z_0}) = f_\theta^{m}\big(f_\theta^{m-1}(\cdots(f_\theta^{1}(\mathbf{z_0})))\big) \triangleq f_\theta(\mathbf{z_0})$$

• 시작을 쉬운 분포 $z_0$ 으로 시작한다.

4. 여러 간단한 invertible layer인 $f_\theta$ 를 여러 레이어로 쌓아서 $f_\theta(\mathbf{z}_0)$ 를 만든다. 그렇게 되면 매우 유연한 transform을 얻을 수 있다. 그리고 $x = z_m$ 이된다. 그럼 위 변환을 change of variable에 적용하게 되면 아래와 같은 수식을 얻을 수 있다.

$$p_X(\mathbf{x};\theta) = p_Z\left( f_\theta^{-1}(\mathbf{x}) \right) \prod_{m=1}^{M}\left| \det\left( \frac{\partial (f_\theta^m)^{-1}(\mathbf{z_m})}{\partial \mathbf{z_m}} \right) \right|$$

5. 각 개별 레이어의 야코비안 행렬식을 얻어 곱하면, 해당 행렬식을 얻을 수 있게 된다. 그리고 각 함수 $f$가 invertible 하기 때문에, $f^{-1}$ 을 계산할 수 있다. 여기서 각 개별 레이어마다 change of variable은 같지만 $\theta$ 는 다르다는 것을 유의해야한다.

---

Learning and Inference

6. 우리는 지금까지 Normalizing Flow 가 어떻게 생겼는지에 대해서 알아왔다. 그럼 어떻게 각 데이터 셋마다 $\theta$ 를 최적화 시킬까? 즉, 학습을 어떻게 할까?

7. 우리는 VAE와는 달리 change of variable 공식 떄문에 $p_\theta$ 에 직접 접근할 수 있기 때문에, AutoRegreesive Model 처럼 특정 데이터 셋의 log-likelihood를 최대화 하는 $\theta$ 를 찾으면 된다. 그래서 log-likelihood의 식은 아래와 같게 표현이 될 수 있다.

$$\max_{\theta} \log p_X(\mathcal{D}; \theta) = \sum_{x \in \mathcal{D}} \log p_Z \big( f_\theta^{-1}(x) \big) + \log \left| \det \left( \frac{\partial f_\theta^{-1}(x)}{\partial x} \right) \right|$$

8. 양쪽 항 다 미분이 가능하기 때문에, gradient인 $\nabla_\theta \log p_X(x;\theta)$ 는 구할 수 있어서 최적화 또한 문제없다.
   • 만약 추론(inference)에서 sampling을 해야된다면 이는, VAE와 같게 $z \sim p_Z(z) \quad x = f_\theta(z)$ 으로 구할 수 있다.
   • z도 latent variable이긴 하지만, VAE의 z와 같은 역할을 한다고 볼 수는 없다. Normalizing Flow에서 z는 x와 차원이 같기 때문이다.
   • 이 과정을 하기 위해서는 $f_\theta$ 를 invertible하고 jacobian 행렬 계산이 용이하도록 parameterized 해야한다. (여러 모델들을 보면서 어떻게 parameterized가 되는지 살펴볼 것이다.)

---

Triangular Jacobian

9. 자, 그럼 지금까지 배운 flow model의 조건들에 대해서 살펴보겠다.
   • p(z) 는 샘플링과, likelihood 계산이 효율적으로 가능한 분포를 선택해야한다.
   • 또한 tractable한 Invertible transformation 을 해야한다.
   • 자코비안 행렬식 계산이 빨라야한다.
     • 기존의 자코비안 행렬식은 nXn 행렬이다. 이는 $O(n^3)$ 의 시간복잡도를 지니고 있다.
     • 따라서 이를 해결하기 위하여 행렬식의 구조를 변형해야한다.

10. 기존 자코비안 행렬식에 시간복잡도가 오래걸린다는 단점을 해결하기 위하여, 기존의 자코비안 행렬식을 먼저 봐보자. 아래의 식과 같다.

$$ x = (x_1, \cdots, x_n) = f(z) = (f_1(z), \cdots, f_n(z)) $$

$$ J = \frac{\partial f}{\partial z} = \begin{pmatrix} \frac{\partial f_1}{\partial z_1} & \cdots & \frac{\partial f_1}{\partial z_n} \\ \vdots & \ddots & \vdots \\ \frac{\partial f_n}{\partial z_1} & \cdots & \frac{\partial f_n}{\partial z_n} \end{pmatrix} $$

11. 위 식에서 우리는 해당 행렬을 상삼각, 하삼각 행렬을 만들면 행렬식의 계산이 $O(n)$ 으로 빨라지게 된다. 그렇게 하기 위해서 가정이 필요하다. 바로 $x_i = f_i(z)$ 가 $z_1, …, z_i$ 까지만 의존하게 된다면 위 행렬식은 하삼각 행렬이 된다.
    • 하삼각 행렬의 determinant는 대각선 원소들의 곱이기 때문에 $O(n)$ 으로 계산이 된다.
    • $x_2 = f_2(z_1, z_2) \quad \Rightarrow \quad \frac{\partial x_2}{\partial z_3} = 0$
    • 만약 상삼각 행렬을 만들고 싶다면 $z_i, …, z_n$ 까지 의존하게 하면 된다.

$$ J = \frac{\partial f}{\partial z} = \begin{pmatrix} \frac{\partial f_1}{\partial z_1} & \cdots & 0 \\ \vdots & \ddots & \vdots \\ \frac{\partial f_n}{\partial z_1} & \cdots & \frac{\partial f_n}{\partial z_n} \end{pmatrix} $$

---

Nonlinear Independent Components Estimation(NICE)

12. 우리는 Normalizing Flow Model의 기본적인 개념에 대해서 알아봤고, 이제 이 개념이 실제 neural network에서 어떻게 쓰이는지 알아볼 것이다. 그 예시 중 첫 번째로 Nonlinear Independent Components Estimation(NICE)에 대해서 알아볼 것이다.

13. NICE에는 두 가지 기능이 있는데, 이 두 가지 기능에 대해서 살펴볼 것이다.

Additive Coupling layers

14. 첫 번째는 Additive Coupling layers이다. 이는 $f_\theta$ 에 비선형성을 부여하기 위한 기능이다. 이 기능은 z를 $\mathbf{z_{1:d}}, \mathbf{z_{d+1:n}}$ 로 2가지의 group으로 나눈다.
    • 이때 $1 \leq d < n$ 이고, d는 임의로 지정되는 인자이다.
    • 각 neural network layer마다 d가 다르다.그러

15. 그럼 이때 우리가 계속 배웠던 Forward Mapping(z->x) 과 Inverse Mapping(x->z)을 살펴보겠다.

• Forward Mapping

  • 앞부분은 그대로 두어 $ \mathbf{x_{1:{d}}} = \mathbf{z_{1:{d}}} $ (Identity Transformation)
  • 뒷부분은 앞부분을 이용해 변환
    $$ \mathbf{x_{d+1:{n}}} = \mathbf{z_{d+1:{n}}} + m_\theta(\mathbf{z_{1:{d}}}) $$
    여기서 $m_\theta(\cdot)$는 파라미터 $\theta$를 가진 신경망이며, 입력 차원은 $d$, 출력 차원은 $n-d$이다.
    • $m$ 을 하나의 layer로 이루어진 MLP라고 생각하면 쉽다.
    • 이로 인해 비선형성이 주어진다.

• Inverse Mapping

  • Forward Mapping에서 덧셈을 사용하였기 때문에, 그 역은 뺄셈만 사용하여 invertible이 쉽게 되는 것을 확인할 수 있다.
  • 앞부분은 그대로 복원 $ \mathbf{z_{1:{d}}} = \mathbf{x_{1:{d}}} $ (Identity Transformation)
  • 뒷부분은 앞부분을 이용해 복원
    $$ \mathbf{z_{d+1:{n}}} = \mathbf{x_{d+1:{n}}} - m_\theta(\mathbf{x_{1:{d}}}) $$

16. 앞선 과정을 거치면 Jacobian 행렬식의 계산이 쉬워지게 된다. Jacobian 식은 다음과 같이 표현될 수 있다. 이유가 궁금하다면 하단의 toggle을 확인하면 좋을 것 같다.

$$ J = \frac{\partial \mathbf{x}}{\partial \mathbf{z}} = \begin{pmatrix} I_d & 0 \\ \frac{\partial \mathbf{x_{{d+1}:n}}}{\partial \mathbf{z_{1:{d}}}} & I_{n-d} \end{pmatrix} $$

자코비안 행렬식 이유

• (위-왼쪽 블록)
  $$ \frac{\partial \mathbf{x_{1:{d}}}}{\partial \mathbf{z_{1:{d}}}} = I_d $$
  (앞부분을 그대로 복사하므로 항등 행렬)

• (위-오른쪽 블록)
  $$ \frac{\partial \mathbf{x_{1:{d}}}}{\partial \mathbf{z_{d+1:{n}}}} = 0 $$ (앞부분 $\mathbf{x}$는 뒷부분 $\mathbf{z}$에 의존하지 않음)

• (아래-왼쪽 블록)
  $$ \frac{\partial \mathbf{x_{d+1:{n}}}}{\partial \mathbf{z_{1:{d}}}} = \frac{\partial \mathbf{x_{{d+1}:n}}}{\partial \mathbf{z_{1:{d}}}} $$ (앞부분 $\mathbf{z}$가 $m_\theta$에 들어가므로 뒷부분 $\mathbf{x}$에 영향을 줌)

• (아래-오른쪽 블록)
  $$ \frac{\partial \mathbf{x_{d+1:{n}}}}{\partial \mathbf{z_{d+1:{n}}}} = I_{n-d} $$
  (뒷부분 $\mathbf{z}$가 그대로 더해졌으므로 미분하면 항등 행렬)

17. 이 행렬은 하삼각 행렬이므로 행렬식은 $\det(J) = \det(I_d) \cdot \det(I_{n-d}) = 1$ 이다.
    • 따라서 이 변환은 Volume Preserving Transformation 이다.
      • 초입방체를 축소하거나 확장하지 않고, 그저 확률 질량만 이동한다.
    • 또한 7번의 maximize log-likelihood 를 떠올려 보면 자코비안 항이 $\log 1 = 0 $ 으로 여러 coupling layer를 쌓아도 상관이 없다는 것을 확인할 수 있다.

Rescaling Layers

18. 여러 Addiitive Coupling Layer가 쌓여서 하나의 NICE를 구성할 것이다. 이때 마지막 layer에서 Rescaling 을 하여 정규화를 한다. 아래는 Rescaling Layer의 Forward Mapping(z->x) 과 Inverse Mapping(x->z)을 나타낸 것이다.

• Forward Mapping
  • 각 차원 $i$에 대해 스케일 $s_i > 0$을 곱해준다. $x_i = s_i z_i$
    • 여기서 $s_i$는 $i$-번째 차원의 scaling factor.
• Inverse Mapping
  • Forward Mapping의 역변환은 나눗셈으로 하면 된다. $z_i = \frac{x_i}{s_i}$
• 자코비안 행렬
  • 자코비안 행렬은 대각선에만 $s_i$ 가 있고 나머지는 0인 대각 행렬이 된다. ($x_i = s_i z_i$ 이기 때문에)
  • $J = \mathrm{diag}(s)$, $\det(J) = \prod_{i=1}^n s_i$ 이다.

19. NICE 모델은 간단하다고 생각할 수 있지만, 실험 결과는 생각보다 좋다. 하지만 z가 x와 같은 차원이다보니 연산량이 많은 모델이기도 하다.

---

Non-volume preserving extension of NICE (Real-NVP)

20. 위의 NICE 모델은 행렬식이 1이어서 Volume Preserving Transformation를 만족한다고 했다. 그렇다면 이동하는 동시에 확장하는 것은 안될까? Real-NVP 에서 그것을 설명한다.

21. 그럼 Real-NVP의 Forward Mapping(z->x) 도 Inverse Mapping(x->z)을 살펴보겠다.

• Forward Mapping
  • 앞부분은 그대로 두어
    $ \mathbf{x_{1:{d}}} = \mathbf{z_{1:{d}}} $ (Identity Transformation)
  • 뒷부분은 scale(α) 과 shift(μ) 를 적용하여 변환
    $$ \mathbf{x_{d+1:{n}}} = \mathbf{z_{d+1:{n}}} \odot \exp(\alpha_\theta(\mathbf{z_{1:{d}}})) + \mu_\theta(\mathbf{z_{1:{d}}}) $$
    여기서 $\mu_\theta(\cdot)$, $\alpha_\theta(\cdot)$는 모두 신경망(MLP)이며,
    입력 차원은 $d$, 출력 차원은 $n-d$이다.
    • $\mu$ : 평행이동(translation) 역할
    • $\alpha$ : 스케일(scale) 조정 역할 (확장을 할 수 있는 역할)
• Inverse Mapping
  • 앞부분은 그대로 복원
    $ \mathbf{z_{1:{d}}} = \mathbf{x_{1:{d}}} $ (Identity Transformation)
  • 뒷부분은 앞부분을 이용해 복원
    $$ \mathbf{z_{d+1:{n}}} = \left(\mathbf{x_{d+1:{n}}} - \mu_\theta(\mathbf{x_{1:{d}}})\right) \odot \exp(-\alpha_\theta(\mathbf{x_{1:{d}}})) $$

22. 또한 Real-NVP의 자코비안 행렬식은 어떻게 계산이 될까? 아래에서 확인해보겠다.

• Jacobian of Forward Mapping

  • Forward mapping의 Jacobian은 블록 삼각행렬 형태가 된다.
    $$ J = \frac{\partial \mathbf{x}}{\partial \mathbf{z}} = \begin{pmatrix} I_d & 0 \\ \frac{\partial \mathbf{x_{d+1:{n}}}}{\partial \mathbf{z_{1:{d}}}} & \text{diag}!\big(\exp(\alpha_\theta(\mathbf{z_{1:{d}}}))\big) \end{pmatrix} $$

  • determinant는 대각 블록의 곱으로 단순화된다.
    $$ \det(J) = \prod_{i=d+1}^{n} \exp(\alpha_\theta(\mathbf{z_{1:{d}}})i) = \exp\Bigg(\sum_{i=d+1}^{n} \alpha_\theta(\mathbf{z_{1:{d}}})_i\Bigg) $$

23. 위 행렬식 $\det(J)$ 을 보면, NICE와 달리 1이 아닌 것을 확인할 수 있다. 따라서 Real-NVP 는 Volume Preserving Transformation 을 만족하지 않고 더욱 유연한 모델이라고 볼 수 있다. 그리고 Real-NVP에서 latent variable z에 대한 보간 실험도 했다. 아래 실험 결과를 보면 latent variable z가 압축적이지 않더라도 보간을 하면 의미 있는 결과를 얻는 것을 확인 할 수 있다. 아래는 Real-NVP 의 모델 실험 결과와 보간 실험이다

---

Continuous Autoregressive models as flow models

24. Normalizing Model의 또 다른 관점은 AutoRegreesive Model을 Normalizing Flow 관점으로 볼 수도 있다는 것이다.

25. 따라서 random variable이 Gaussian에서 연속적일 때의 AR의 식을 아래와 같이 설정할 수 있고, 각 조건부 확률 분포 또한 표현하면 아래와 같다.

$$p(\mathbf{x}) = \prod_{i=1}^n p(x_i \mid \mathbf{x_{<i}})$$ $$p(x_i \mid \mathbf{x_{<i}}) = \mathcal{N}\big(\mu_i(x_1, \cdots, x_{i-1}), ; \exp(\alpha_i(x_1, \cdots, x_{i-1}))^2\big)$$

• $\mu_i(\cdot)$ : 평균을 출력하는 네트워크 (혹은 함수)
• $\alpha_i(\cdot)$ : 로그 분산을 출력하는 네트워크 (혹은 함수)

26. 이 AR 모델을 sampling을 한다면 아래와 같이 결정론적으로 계산할 수 있다. (이는 AR을 Flow Model의 특성을 띄게 하는 중요한 부분이다.)

    • 우선 $z_i \sim \mathcal{N}(0,1)$에서 표준정규분포 샘플을 얻습니다. 그 다음 $x_i$를 재구성할 수 있습니다.

    • 첫 번째 Sampling: $x_1 = \exp(\alpha_1) z_1 + \mu_1$

    • 두 번째 Sampling: $x_2 = \exp(\alpha_2(x_1)) z_2 + \mu_2(x_1)$

    • 세 번째 Sampling: $x_3 = \exp(\alpha_3(x_1, x_2)) z_3 + \mu_3(x_1, x_2)$

27. 따라서, 위의 AR 모델이 Flow Model로 해석될 수 있다는 것을 알 수 있다. 왜냐하면 기본 분포(latent variable z)로 부터 invertible transformation을 통하여 데이터 (x)를 AR처럼 만들어 내기 때문이다.
    • 따라서 이렇게 표현하면 AR은 Flow Model의 한 종류라고도 볼 수 있게 된다.

Masked Autoregressive Flow (MAF)

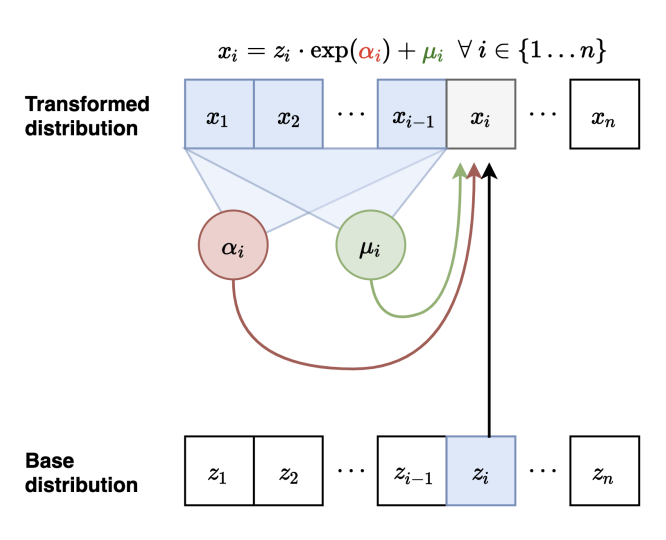
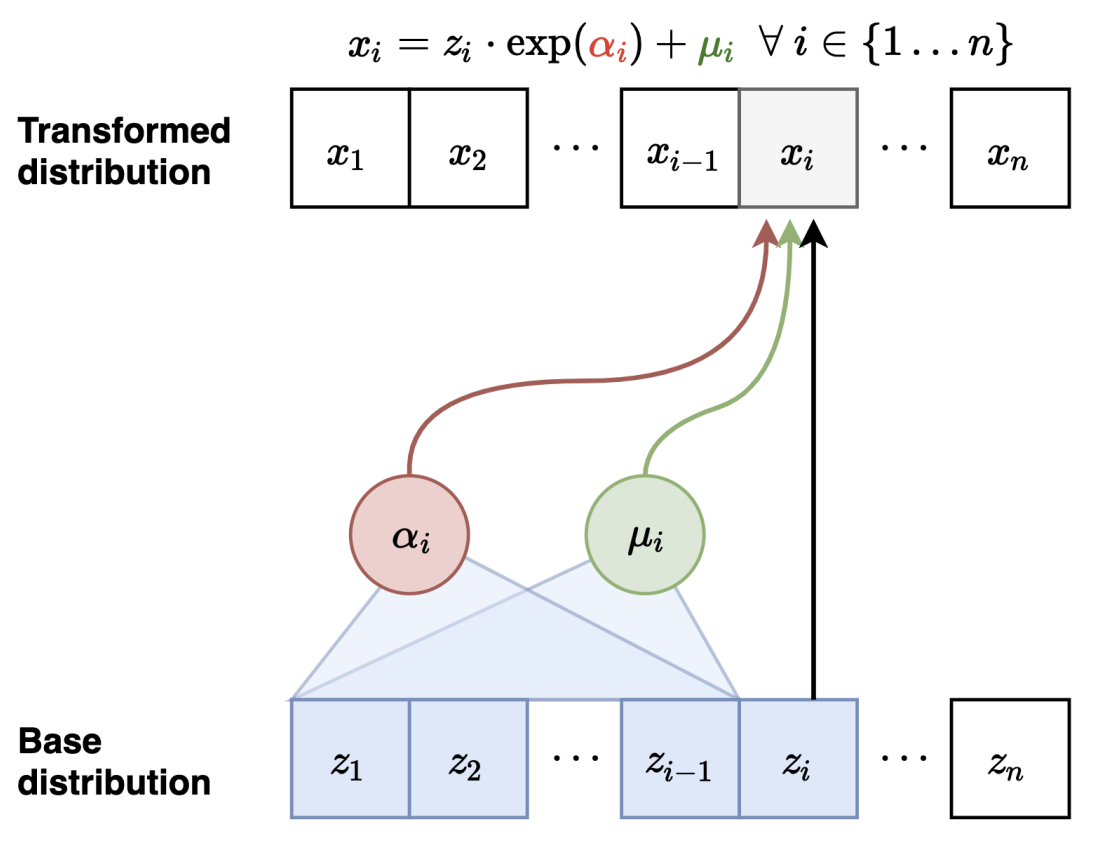
28. 위에서 봤던 구조를 직접 사용한 모델인 MAF에 대한 설명이다.

• Forward Mapping

  • 첫 번째 변수 변환: $ \mathbf{x_1} = \exp(\alpha_1) \cdot z_1 + \mu_1 $
    이때 $\mu_2(x_1), \alpha_2(x_1)$를 계산한다.

  • 두 번째 변수 변환: $ \mathbf{x_2} = \exp(\alpha_2) \cdot z_2 + \mu_2 $
    이때 $\mu_3(x_1, x_2), \alpha_3(x_1, x_2)$를 계산한다.

  • 이런 식으로 반복하여 $x_i$를 순차적으로 계산한다.

  • 여기서,

    • $\mu$ : 평행이동(translation) 역할
    • $\alpha$ : 스케일(scale) 조정 역할 (확장/축소 가능)

• Inverse Mapping

  • 학습할때 모든 $\mu_i, \alpha_i$를 먼저 계산 가능(e.g., MADE를 사용하여 병렬적으로 가능)
    • 학습이기 때문에 모든 $x_i$를 알 수 있기 ㅇ때문이다. (for)
  • 첫 번째 변수 복원: $ \mathbf{z_1} = \frac{x_1 - \mu_1}{\exp(\alpha_1)} $
  • 두 번째 변수 복원: $ \mathbf{z_2} = \frac{x_2 - \mu_2}{\exp(\alpha_2)} $
  • 세 번째 변수 복원: $ \mathbf{z_3} = \frac{x_3 - \mu_3}{\exp(\alpha_3)} $
  • 이런 식으로 $z_i$를 순차적으로 복원한다.

• Jacobian

  • 야코비안 행렬은 다른 flow model과 마찬가지로 lower diagonal이다. 따라서 계산이 수월하다.

29. MAF에서 $\alpha, \mu$의 계산은 MADE(네트워크에 마스크를 씌워서 특정 $i$ 까지만 의존하게 만드는 구조)와 같은 네트워크를 사용해서 $x_{1:i-1}$ 만 의존할 수 있도록 하고 병렬적으로 한번에 구할 수 있다. 하지만 결국 구조적 문제 때문에, MAF에서 Sampling을 할 땐 $z_1$ 만 구할 수 있으니까 Autoregressive 하게 $x_i$ 까지 계산을 해야되서 시간 복잡도가 $O(n)$ 이 걸리는 단점이 있다. 이를 해결하기 위하여 MAF가 아닌 Inverse Autoregressive Flow (IAF)가 나오게 되었다.

Inverse Autoregressive Flow (IAF)

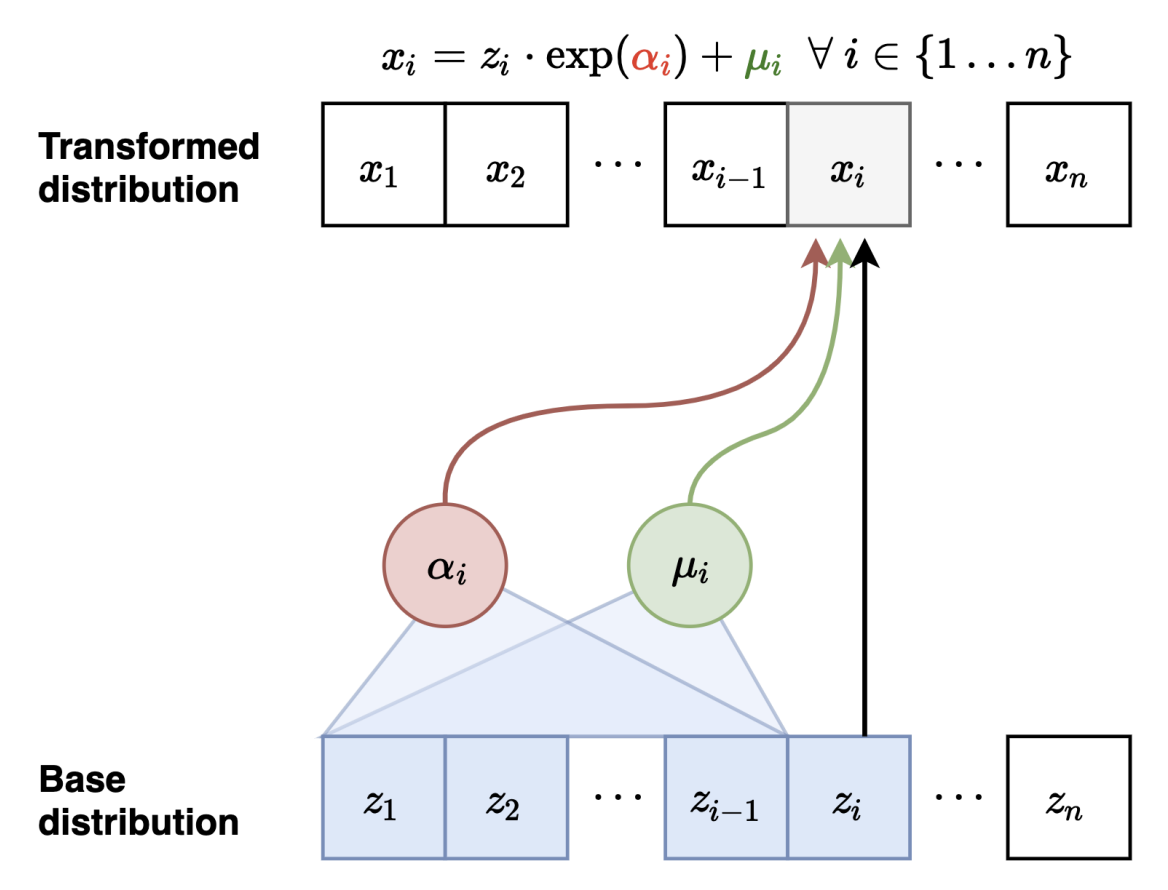
30. IAF에서는 MAF와 달리, 네트워크에 들어가는 입력을 z로 변환시켰는데, 이것이 가능한 이유는 MAF에서 보여준 network들은 invertible network이기 때문에 사실 입력, 출력이 무엇인지 상관이 없기 때문이다.

• Forward Mapping

  • 첫 번째 변수 변환: $ \mathbf{x_1} = \exp(\alpha_1)\cdot z_1 + \mu_1 $
  • 두 번째 변수 변환: $ \mathbf{x_2} = \exp(\alpha_2(z_1))\cdot z_2 + \mu_2(z_1) $
  • 세 번째 변수 변환: $ \mathbf{x_3} = \exp(\alpha_3(z_1,z_2))\cdot z_3 + \mu_3(z_1,z_2) $
  • 여기서,
    • $\mu$ : 평행이동(translation) 역할
    • $\alpha$ : 스케일(scale) 조정 역할 (확장/축소 가능)
    • 모든 $z_i$는 base 분포에서 동시에 샘플 가능.
    • $\mu_i(\cdot), \alpha_i(\cdot)$는 **$z_{1:i-1}$**에만 의존하도록 마스킹된 네트워크가 한 번에 전부 출력할 수 있으므로,
      실제 구현에서는 $x_1,\dots,x_n$을 병렬적으로 한 번에 계산할 수 있다.

• Inverse Mapping (x → z, 학습/likelihood 계산 시 사용)

  • 이 방향에서는 $\mu_i, \alpha_i$가 **$z_{1:i-1}$**에 의존하므로, 모두를 미리 병렬 계산할 수 없다.
    따라서 $z_i$를 순차적으로 복원해야 한다.
  • 첫 번째 변수 복원: $\mathbf{z_1} = \frac{x_1 - \mu_1}{\exp(\alpha_1)} $
  • 두 번째 변수 복원 : $\mathbf{z_2} = \frac{x_2 - \mu_2(z_1)}{\exp(\alpha_2(z_1))} $
  • 세 번째 변수 복원 : $\mathbf{z_3} = \frac{x_3 - \mu_3(z_1,z_2)}{\exp(\alpha_3(z_1,z_2))} $

31. 따라서 우리가 원하는 Sampling($x_i$가 나오기)을 할 때는 꽤 빠르다. 하지만 IAF도 역시 단점이 있다. 바로, x->z가 필요한 상황에서는 느리다는 것이다.
    • x->z가 필요한 상황은 모델을 훈련시키고 싶어서 maximum likelihood train이 필요할 때이다.
    • 이미지(x)에서 z로 갈 수 있어야 훈련이 가능하기 때문이다. 모든 데이터 포인트에서 이를 수행해야한다. 그럴 때 모든 데이터 포인트 (x)에 대하여 매핑되는 z를 구해야 하기 때문에, 모두 계산을 해야한다.
    • 하지만 만약, forward 단계에서 z를 cache한다면 해결이 될수도 있다고 한다.

Parallel Wavenet

32. MAF와 IAF를 요약 비교해보자.

• MAF: Likelihood 계산은 빠르지만 샘플링이 느리다. → **훈련(MLE, 밀도추정)**에 적합
• IAF: 샘플링은 빠르지만 Likelihood 계산이 느리다. → 실시간 생성에 적합

33. 그렇다면 MAF와 IAF의 장점을 모두 사용할 수 있는 방법은 없을까? 이 질문에 대한 방법은 있다. 바로 교사 모델은 MAF로 훈련하여 효율적인 훈련을 하고, 그 모델을 distillation하고, 학생 모델을 IAF 구조로 하여 학생 모델으로 sampling을 진행하면 매우 효율적인 프레임워크를 얻을 수 있다. 이것이 Parallel Wavenet이다.

$$D_{KL}(s, t) = \mathbb{E_{x \sim s}}\left[ \log s(x) - \log t(x) \right]$$

34. 위 식은 Parallel Wavenet의 목적식인데, s->t로 진행하면서 많은 이점을 얻을 수 있게 된다. 해당 목적 함수로 최적화를 진행할 때, 많은 sampling 과정을 거쳐야하는데 student 모델은 sampling이 teacher 보다 수월하기 때문에 효율적이다. 따라서 해당 목적식을 거치면 학생 모델의 분포가 교사 모델의 분포를 닮게 된다.
    • 아래는 Parallel Wavenet의 전체 흐름이다.
      • 훈련
        • Step1: Teacher 훈련
        • Step2: Student 훈련 (KL 목적식 사용) -> (Teacher는 fixed)
      • 추론
        • Only Student (Sampling이 빨라서)

35. 그 다음 Normalizing Flow의 여러 모델들을 간단히 살펴 보았는데, MintNet, Gaussianization Flows 을 살펴보았다. 자세한건 논문을 살펴보면 될 것 같고, Gaussianization Flows에서 사용된 Inverse CDF Trick이 중요해보여서 아래 사이트에서 참고하여 공부하면 좋을 것 같다.

• Inverse CDF Trick이란 Uniform 분포에서 특정한 분포(예: Gaussian)로 변환이 되는 분포이다.
  • 컴퓨터의 난수 생성기는 보통 Uniform이기 때문에 특정 분포를 띄고 싶을때 유용하게 사용된다.
• Inverse CDF Trick 참고 자료

---

Reference

• https://deepgenerativemodels.github.io/
• https://www.youtube.com/watch?v=qgTvgBCOyn8&list=PLoROMvodv4rPOWA-omMM6STXaWW4FvJT8&index=9
• https://deepseow.tistory.com/45
• https://domybestinlife.tistory.com/348