[CS236] 7. Normalizing Flows - 1
개요
- 이번 포스트에서는
CS236강의의7강뒤부분을 설명한다.
- 이전 포스트에서는
Latent Variable Models중VAE에 대한 내용을 배웠다. VAE는 $p_\theta(x) = \int p_\theta(x,z)dz$ 으로 모든 z에 대한 계산이 어렵다는 단점이 있다. (우리는 이 단점을ELBO로 해결을 했었다.) 그렇기 때문에 이번 포스트에서는VAE말고latent variable z를 사용한 다른 생성 모델을 살펴볼 것이다.
- 기존
VAE는neural network를 통해 x를 구했다. ($p(x|z) = \mathcal{N}(\mu_\theta(z), \Sigma_\theta(z))$) 하지만 이 방법은 확률론적이기 때문에, 같은 z여도 다른 x를 내놓을 수 있다. 하지만Latent Variable Models중 하나인Flow Model은 $x = f_\theta(z), z = f_\theta^{-1}(x)$ 로 invertible 하고 결정론적인 함수를 도입한다.- 해당 함수를 사용하면 x에 대응하는 오직 고유한 z가 있기 때문에, 더이상 모든 z에 대한 계산을 할 필요가 없어진다. (no enumeration)
- 기존
VAE는 모든 z를 계산할 수 없기 떄문에, 정보의 손실이 있을 수 있지만 Flow Model을 사용한다면, 고유한 z와 x가 있기 때문에 정보의 손실이 없다.
Change of Variables 공식
Flow Model에 들어가기 앞서, 필요한 기본적인 개념들을 정리할 필요가 있다.
-
연속 확률 변수(Continuous Random Variable) X에 대한 기본 개념을 아래와 같이 정리할 수 있다.
연속 확률 변수 기본 개념
-
X를 연속 확률 변수라고 하자.
-
누적 분포 함수(Cumulative Distribution Function, CDF)는 다음과 같이 정의된다:$$F_X(a) = P(X \leq a)$$
-
확률 밀도 함수(Probability Density Function, pdf)는 누적 분포 함수의 도함수로 표현되며 다음과 같다:CDF는 누적된 확률을 나타내는 함수이기 때문에, 특정 값에서 값이 얼마나 자주 나오는지에 대한 정보를 직접적으로 알 수 없다.- 따라서
CDF를 미분함으로써 변화율을 얻고, 특정 값 주변 구간에서 값이 얼마나 자주 발생하는지를 나타내는 확률 밀도 함수(pdf) 를 정의한다.
$$p_X(a) = F’_X(a) = \frac{dF_X(a)}{da}$$
-
실제로는 특정한 분포 형태(parameterized densities)를 가정하고 사용하게 되며, 대표적으로는 다음과 같은 분포들이 있다:
- Gaussian 분포 (정규분포): 확률 밀도 함수는 다음과 같다: $$X \sim \mathcal{N}(\mu, \sigma), \quad p_X(x) = \frac{1}{\sigma \sqrt{2\pi}} \exp\left( -\frac{(x - \mu)^2}{2\sigma^2} \right)$$
- Uniform 분포 (균등분포): 확률 밀도 함수는 다음과 같다:$$X \sim \mathcal{U}(a, b), \quad p_X(x) = \frac{1}{b - a} \cdot \mathbf{1}[a \leq x \leq b] $$
-
-
X가 단일 스칼라 값이 아닌 연속 확률 벡터(즉, 다변량 확률 변수)인 경우에는, 공동 확률 밀도 함수(Joint Probability Density Function)를 사용한다.
-
예를 들어, 다변량 정규분포(Multivariate Gaussian)의 경우 확률 밀도 함수는 다음과 같다:
$$p_X(\mathbf{x}) = \frac{1}{\sqrt{(2\pi)^n |\Sigma|}} \exp\left( -\frac{1}{2} (\mathbf{x} - \mu)^T \Sigma^{-1} (\mathbf{x} - \mu) \right)$$
- ( \mu )는 평균 벡터
- ( \Sigma )는 공분산 행렬
- ( n )은 차원 수
-
-
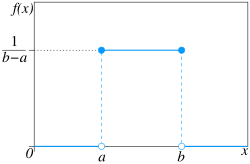
- 만약 z가 [0,2] 구간에서 uniform random variable 이라고 가정하자. 이때 PDF는 $p_z$ 이다. 그렇다면 $p_z(1)$ 은 무엇일까?
- $p_z(1) = \frac{1}{2}$ 이다. (모르겠으면 위 기본 개념을 살펴보면 될 것 같다.)
- 이때 $x = 4z$ 라고 한다면 $p_x(4)$ 는 무엇일까?
- $p_x(4) = p(x = 4) = p(4z = 4) = p(z = 1) = p_z(1) = \frac{1}{2}$ 일까? 아니다.
- x는 [0,8] 구간에서 uniform random variable이므로, $p_x(4) = \frac{1}{8}$ 이다.
- 이는,
확률 밀도 함수(PDF)에서 단순히 값을 대입하는것이 아니라 변화율을 고려해야한다는 직관을 보여준다. - 이를 해결하기 위하여 variable을 변경하는 공식을 대입해보자.
- 만약 $X= f(Z)$ 이고 f가 단조함수라면 $Z = f^{-1}(X) = h(X)$ 라고 표현할 수 있을 때 공식은 아래와 같다.
$$p_X(x) = p_z(h(x))|h^{\prime}(x)|$$
-
이게 확률 자체가 아니라
PDF이기 때문에 위의 공식을 적용해야한다.PDF는 “면적을 길이당 확률로 나눈 값"이라서, 변수 변환으로 길이가 늘어나면, 그 구간에 퍼진 확률은 같아야 하니까 밀도는 도함수만큼 줄어야 확률 질량이 보존된다. 따라서 $X = 4Z$ 의 문제는 위 공식으로 해결이 가능하다.직관적인 개념과 증명
-
조금 더 직관적으로 이해하기 쉽게 풀어볼 것이다.
-
우리는 X에 대한 $p_x(x)$ 를 구하고 싶다.
-
하지만 지금 우리가 아는 분포(언어)는 Z이다. 따라서, 확률 밀도 Z에서 X에 대한 밀도 정보를 가져와보자.
- $Z = f^{-1}(X) = h(X)$ 처럼, 역함수를 사용하면 X를 Z의 언어로 바꾸어 표현이 가능하다.
- 그럼 이것을 $p_Z(Z)$ 에 넣어 해당 정보를 얻을 수 있다.
-
그리고 이것을 다시 X의 규모로 조정을 해야한다.
- $\frac{dz}{dx}$ , 즉, X가 변할 때 Z의 변화량을 곱하면서 스케일 조정이 가능하다.
-
그렇다면, 정확한 증명은 아래 사진과 같다.
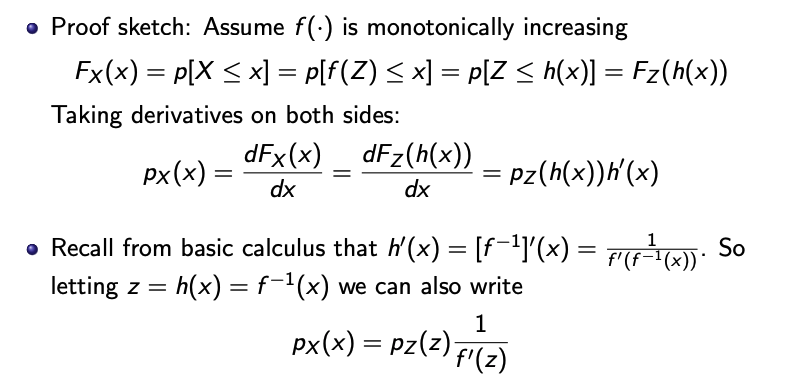
-
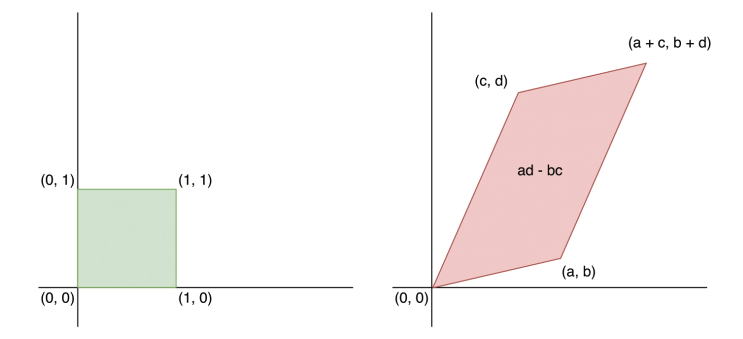
- 그럼 단순한 스칼라 값이 아니라 vector일 때를 살펴보겠다. 어떤 균등 분포 $[0,1]^n$ 에 있는 Z가 있다고 했을 때 $n = 2$인 2차원이라면 좌표평면에서 정사각형의 형태이다. 하지만 invertible한 행렬 A를 $X = AZ$ 로 한다면 X는 평행사변형이 된다.
- 이때 평행사변형의 부피는 $|det(A)|$ 로 구할 수 있다. (기하학적인 증명에 의하여)
- 우리는 X로 변환한다면 해당 부피가 얼마나 줄어들거나 늘어나는지에 대한 스케일을 조정해야한다.
- 따라서 $W = A^{-1}$ 라고 하면 우리는 아래와 같은 식을 얻을 수 있다.
$$ \begin{aligned} p_X(x) &= p_Z(Wx) / |det(A)| \\ &= p_Z(Wx) |det(W)| \end{aligned} $$
- $W = A^{-1}$ 일 때, $det(W) = \frac{1}{det(A)}$ 을 만족한다.
- 이제 일반적인 상황을 살펴보자. 지금까지는 선형 변환을 하는 A를 다루었다. 하지만, 우리는 비선형적인 구조인
neural network를 사용하므로 비선형 변환에서 variable change가 어떻게 이루어지는지 확인할 필요가 있다.
-
비선형변환을 하면 각 점마다 국소적 선형 변환을 하여 해당 부피 변화율을 구해야하는
자코비안 행렬을 사용해서 값을 구하게 된다. 비선형 변환일 때의 variable change 식은 아래와 같다.자코비안 행렬에 대해서
자코비안 행렬
- 행렬에서
선형 변환은 항상 원점을 지나면서 좌표계가 일정하게 바뀌는 것을 의미하지만비선형 변환은 위치에 따라 원점을 보존하지 않고 좌표계를 뒤틀거나 휘게 만들 수 있다. - 따라서 x,y 좌표계에서 u,v 좌표계로
선형변환을 하면 두 좌표계를 번갈아서 이동할 수 있지만, 만약 변환이비선형적이라면 하지못한다. 이때 나온게Jacobian 행렬이다. - 이 행렬은
비선형 변환을 거친 좌표계에서 국소적으로 점마다 선형변환으로 근사할 수 있다. - 아래는
(u,v)좌표계를비선형 변환을 하여(x,y)로 만들었을 때 J 행렬을 나타낸다. $$ J = \begin{bmatrix} \frac{\partial x}{\partial u} & \frac{\partial x}{\partial v} \\ \frac{\partial y}{\partial u} & \frac{\partial y}{\partial v} \end{bmatrix} $$
자코비안 행렬식
비선형 변환을 이용해서 도형의 부피(넓이)를 구하려고 할 때, 선형적 공간에서 부피(넓이)를 구하고 각 point 별로 늘어진 만큼 보정해주면 된다.- 따라서
(u,v)좌표계에서(x,y)좌표계로 변환 될 때 행렬식 관계는 다음과 같다. $$dx \ X \ dy = |J|(du \ X \ dv)$$
- 행렬에서
$$p_X(\mathbf{x}) = p_Z\left( f^{-1}(\mathbf{x}) \right) \left| \det\left( \frac{\partial f^{-1}(\mathbf{x})}{\partial \mathbf{x}} \right) \right|$$
- f가
neural network라고 생각하면 된다.
$$p_X(\mathbf{x}) = p_Z(\mathbf{z}) \left| \det\left( \frac{\partial \mathbf{f}(\mathbf{z})}{\partial \mathbf{z}} \right) \right|^{-1}$$
- $det(A^{-1}) = det(A)^{-1}$ 으로, 공식을 두가지를 사용할 수 있다.
- x와 z는 같은 차원이다.
-
이제 이 general한 공식을 가지고 2차원 확률 변수에서 예를 들어 보겠다.
- $Z_1$과 $Z_2$는 연속 확률변수이고, 결합밀도 $p_{Z_1,Z_2}$를 가짐
- $u : \mathbb{R}^2 \to \mathbb{R}^2$ 는 가역 변환(invertible transformation)
- 입력 2개 $(Z_1, Z_2)$를 받아 출력 2개 $(u_1, u_2)$를 생성
- 헷갈릴 수 있는데, u는 2개의 함수를 묶어서 벡터 형태로 만든
벡터값 함수이다. 따라서 u1, u2는 각각 함수라고 생각하면 된다. - $u = (u_1, u_2)$
- $v = (v_1, v_2)$는 $u$의 역변환
- $X_1 = u_1(Z_1, Z_2)$, $X_2 = u_2(Z_1, Z_2)$라고 하면
- $Z_1 = v_1(X_1, X_2)$, $Z_2 = v_2(X_1, X_2)$ 으로도 나타낼 수 있다.
- 이제 $p_{X_1, X_2}(x_1, x_2)$ 를 구해보자면 아래와 같다.
$$ \begin{aligned} p_{X_1, X_2}(x_1, x_2) &= p_{Z_1, Z_2}\big(v_1(x_1, x_2), v_2(x_1, x_2)\big) \left| \det \begin{bmatrix} \frac{\partial v_1(x_1, x_2)}{\partial x_1} & \frac{\partial v_1(x_1, x_2)}{\partial x_2} \\ \frac{\partial v_2(x_1, x_2)}{\partial x_1} & \frac{\partial v_2(x_1, x_2)}{\partial x_2} \end{bmatrix} \right| \\ &= p_{Z_1, Z_2}(z_1, z_2) \left| \det \begin{bmatrix} \frac{\partial u_1(z_1, z_2)}{\partial z_1} & \frac{\partial u_1(z_1, z_2)}{\partial z_2} \\ \frac{\partial u_2(z_1, z_2)}{\partial z_1} & \frac{\partial u_2(z_1, z_2)}{\partial z_2} \end{bmatrix} \right|^{-1} \end{aligned} $$
- 첫번째항이
inverse term이고 두번째 항이forward term이다.
- 다음 lecture에서 이제 이 공식을 가지고 실제
생성 모델을 만들어볼 것이다.