[CS236] 5. Latent Variable Models-1

GoodYoung included in DL Theory Lecture Deep Generative Models

2025-07-14 1485 words 7 minutes

Contents

개요

이번 포스트에서는 CS236 강의의 5강 내용을 정리한다.

Autoregressive 구조는 장/단점을 지닌다. 장점은 likelihood를 평가하여 maximum likelihood를 구할 수 있어 훈련이 비교적 쉽다.

반면, 단점은 순서대로 생성하여 생성 시간이 오래걸린다. 그리고 비지도 학습을 사용하여 데이터의 특징을 추출하는 것이 명확하지 않다. 이 점이 잠재 변수 모델을 사용해서 해결할 수 있는 일 중 하나이다.

이번 챕터에서는 이 latent variable(잠재 변수)가 있을 때 생성 모델이 추론과 학습을 수행하는 방법에 대해서 설명할 것이다.

Latent Variable Model

위 그림과 같이 사람 이미지와 같은 이미지 데이터 안에는 단순히 픽셀 데이터가 아니라 그 안에 성별, 눈 색깔 등의 여러 변동성 큰 정보들이 포함되어 있다. 하지만 이 모든 정보들을 annotated 하여 이용하기 쉽지 않다. 그렇기 떄문에 latent variable에 원본 데이터 상에 숨겨진 특징들이 존재하게 된다.

만약 특정한 특징을 나타내는 latent variable(z)을 사용하여 생성하게 되면, 우린 더욱 더 유연한 생성 모델을 얻을 수 있을 것 이다.

그래서 이 latent variable(z)을 반영하여 모델의 확률 분포 $p(x,z)$를 구하는 Latent Variable Model에 대해서 알아볼 것이다.

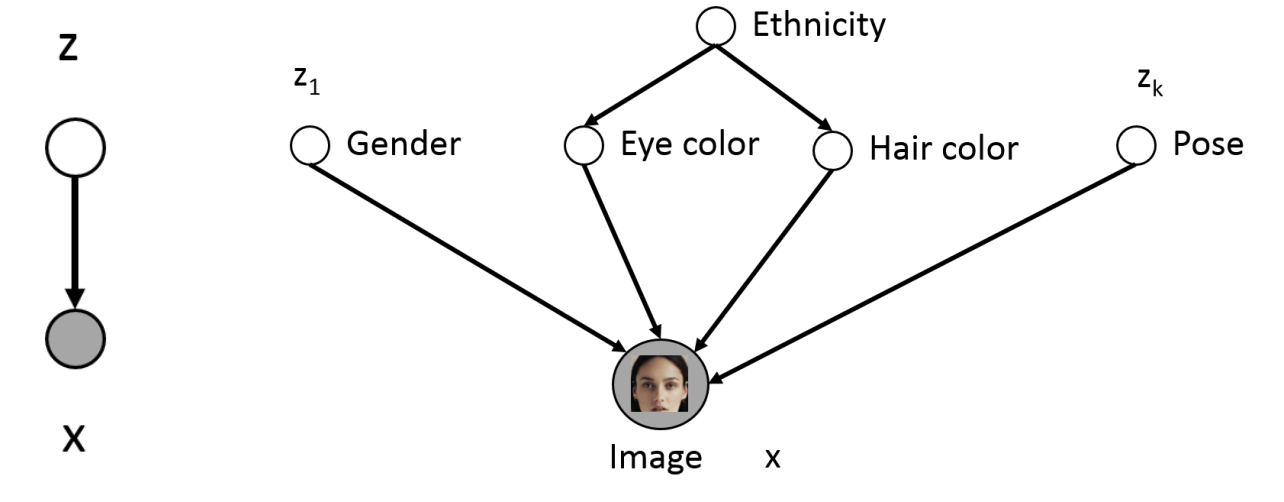
왼쪽 그림은 Latent Variable Model을 간략하게 나타낸 구조이고 오른쪽 그림은 베이지안 네트워크일 때를 나타낸다.

우리는 $x$와 $z$의 결합 분포인 $p(x,z) = p(z)p(x|z)$ 를 구하게 될 것이고 이것이 베이지안 네트워크로 가면 $p(x,z) = p(z_1)p(x|z_1)+…+p(z_k)p(x|z_k)$ 가 될 것이다.

이렇게 잠재변수 z를 포함한 모델링을 사용하면 x만을 활용한 것보다 쉽다. 또한 만약 z의 특징을 각각 추출할 수 있다면, 그것을 이용해서 다른 종류의 task에도 이용이 가능하다. (ex)eyeColor = Blue만 식별 가능)

하지만 현실적으로 모든 z중에 특정 z만 따로 추출하는 것이 어렵다는 것이다.(이 말은 위에서 현실적으로 모든 z의 확률을 구할 수 없어서 베이지안 네트워크를 사용하기 어려울 수 있다는 말과 동일하다.)

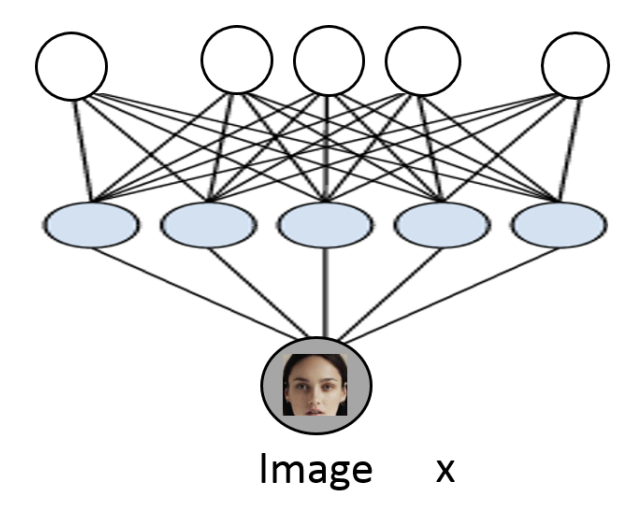
따라서 우리는 이 문제를 해결하기 위하여 단순한 z(가우시안) 만을 가정하여 deep neural network(모든 각각의 관계의 정보를 따로따로 확인하지 않아도 모든 정보를 고려해줄 수 있다.) 를 사용하여 이 z를 예측하려고 한다.

$z \sim \mathcal{N}(0,1)$
$p(x|z) = \mathcal{N}(\mu_\theta(z), \Sigma_\theta(z))$
이 문제는 비지도학습의 representation learning이기 때문애 학습 시 z에 대해서 잘 학습(z의 특징을 잘 추출)되기를 희망하게 된다. (이 모델이 어떤 z를 추출할지 명확하지 않다.)
만약 학습이 잘된다면, z의 분포를 클러스터링 하여 우리가 원하는 클러스터에 해당하는 z의 값($p(z)$)을 구할 수 있고 이 z를 가지고 새로운 데이터 $p_\theta(x,z)$를 만들어낼 수 있게 된다. 다음 챕터에서 이에 대해 더 자세히 설명할 것이다.

Mixture of Gaussians (GMM,VAE)

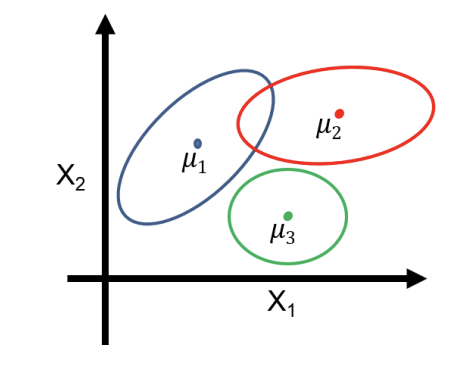
그렇다면 z를 어떻게 예측 하는 방법에 대해서 자세히 알아볼 필요가 있다. 데이터의 분포를 확인하면 위 그림과 같을 것이다. 그 후, $K$개의 가우시안 분포(혼합 성분)를 나눌 수 있다. 그럼 생성 과정에선 K개 중 하나를 선택하여 그 K에 해당하는 평균, 공분산을 따르는 가우시안 분포에서 x를 샘플링한다. (이는 VAE에서 생성 과정에서도 동일하다.)

$\mathbf{z} \sim \text{Categorical}(1, \cdots, K)$
$\mathbf{x} \sim p(\mathbf{x} \mid \mathbf{z} = k) = \mathcal{N}(\mu_k, \Sigma_k)$ (likelihood)

이 방법은 생성 과정 뿐 아니라, x가 주어졌을 때 어떤 z에 속하는지 맞출 수 있는 추론 과정에도 (posterior $p(z|x)$) 사용할 수 있다. (clustering, unsupervised representation learning)

또한 Mixture of Gaussians의 전체 확률 ($p(x)$)도 구할 수 있는데 다음과 같은 식으로 가능하다.

$p(\mathbf{x}) = \sum_{z} p(\mathbf{x}, z) = \sum_{z} p(z) \cdot p(\mathbf{x} \mid z) = \sum_{k=1}^{K} p(z=k) \cdot \mathcal{N}(\mathbf{x}; \mu_k, \Sigma_k)$
이때 얻을 수 있는 직관은 simple한 $p(x|z)$를 활용하여 복잡한 혼합 모델($p(x)$)을 구할 수 있다는 것이다.

지금까진 z를 어떻게 예측을 할지에 대해서 알아보았다. 이 Mixture of Gaussians에서는 Neural Network(NN)를 사용하지 않아 z의 수가 많아지면 계산하기 어려운 단점이 있다. 그럼 우린 이 z를 가지고 deep neural network를 사용한 VAE에서 어떻게 활용이 되는지 알아볼 필요가 있다.

Mixture of Gaussians에서는 NN을 사용하지 않기 때문에 임의의 k에 따른 평균과 표준편차를 조회 테이블에서 각각 구할 수 있다. 하지만 VAE에선 유한한 수의 k개를 구하지 않아도 된다.

무한한 수의 혼합 성분(각각 가우시안을 가지는)이 있다고 생각 해도 된다.
$\mathbf{z} \sim \mathcal{N}(1, I)$
$p(x|z) = \mathcal{N}(\mu_\theta(\mathbf{z}), \Sigma_\theta(\mathbf{z}))$

또한 z를 샘플링 하고 z를 neural network에 넣어 가우시안 요소에 대한 평균, 표준편차를 구할 수 있다.

VAE의 생성 과정은 GMM과 동일하다. 구성 요소($K$)를 정하고 z값을 샘플링한다. 그 다음 z에 맞는 평균, 표준편차를 구한 다음(neural network를 통하여) x를 샘플링 하는 과정으로 진행된다.

Maximum Marginal Likelihood

만약 훈련 때 위 그림 처럼 어떤 pixel이 보이지 않을 경우를 생각해보자. 이때 $\mathbf{X}$ 를 관측된 부분이라고 하고 $\mathbf{Z}$ 를 관측되지 않은 초록색 영역이라고 하자.

pixel cnn처럼 autoregressive model은 안보이는 나머지 부분을 포함한 전체 결합 확률 분포를 다음과 같이 정의할 수 있다. $p(\mathbf{X},\mathbf{Z};\theta)$

우리는 관측된 $\mathbf{X}$ 만을 사용하여 모든 가능한 $\mathbf{Z}$ 를 구해야한다. 그렇게 하기 위하여 우리는 marginal likelihhod를 구해야 한다.

모든 가능한 $\mathbf{Z}$ 를 고려해서 합산해야 한다.
$p(\mathbf{x}) = \sum_{z} p(\mathbf{x}, z) = \sum_{z} p(z) \cdot p(\mathbf{x} \mid z)$
하지만 여기 z가 고차원이라면 이 것을 계산하는데 엄청난 비용이 들 수 있다.

만약 Variational Autoencoder의 경우라도 위와 비슷하다. 훈련 시간에 z가 관찰되지 않고 특정 x를 관찰할 확률을 평가하려면 z가 취할 수 있는 모든 가능한 값을 살펴보고 얼마나 x를 생성할 가능성이 있는지 알아봐야한다.

z는 연속확률분포 이므로, 모든 가능한 z의 값들을 적분해야한다.

$\mathbf{z} \sim \mathcal{N}(1, I)$
$p(x|z) = \mathcal{N}(\mu_\theta(\mathbf{z}), \Sigma_\theta(\mathbf{z}))$
$p(\mathbf{x}) = \int p(\mathbf{x}, z) , dz = \int p(z) \cdot p(\mathbf{x} \mid z) , dz$
VAE 또한 z의 차원이 증가할수록 엄청난 비용이 든다.

따라서 우리는 훈련을 할 때 특정 데이터 셋을 생성할 확률 ($p(x)$)를 최대화 하는 매개변수를 찾으려고 할 것이다. 이때 autoregressive model처럼 x변수만 있는 것이 아니라, x와 z가 있기 때문에 Maximum Marginal Likelihood로 계산해야한다.

$$\log \prod_{x \in \mathcal{D}} p(x; \theta) = \sum_{x \in \mathcal{D}} \log p(x; \theta) = \sum_{x \in \mathcal{D}} \log \sum_{z} p(x, z; \theta)$$

하지만 계속 한계점을 언급했던 것 처럼 $\log \sum_{z} p(x, z; \theta)$ 는 z의 차원이 커질수록 계산이 불가능 하다.

더불어, z가 연속형이어도 적분을 사용해야하기 때문에 계산하기 어렵고, gradient도 계산하기 어렵다.
그래서 아주 저렴한 approximation 방법이 필요하다.

Naive Monte Carlo

$$p_\theta(x) = \sum_{\text{All values of } z} p_\theta(x, z) = |\mathcal{Z}| \sum_{z \in \mathcal{Z}} \frac{1}{|\mathcal{Z}|} p_\theta(x, z) = |\mathcal{Z}| \mathbb{E_{z \sim \text{Uniform}}(\mathcal{Z})} \left[ p_\theta(x, z) \right]$$

$$\sum_{z} p_\theta(x, z) \approx |\mathcal{Z}| \cdot \frac{1}{k} \sum_{j=1}^{k} p_\theta(x, z^{(j)})$$

몇가지 가능한 대안 중 하나가 Naive Monte Carlo이다. 모든 z에 대한 계산을 하는 것이 아니라, monte carlo를 사용하여 몇개의 z만 가지고 근사값을 계산할 수 있다.

위에서 본 marginal likelihood의 식에서 평균의 형태로 바꾸고, 그것을 기대값으로 표현한 식(3)으로 변경하면 monte carlo 샘플링으로 근사가 가능한 형태로 변형이 된다.

Monte carlo는 기대값을 샘플들의 평균으로 근사할 수 있게 한다.

하지만 단순하게 z에 대하여 uniform 샘플링을 하면 variance가 크고 모델이 불안정하다. 따라서 더욱 똑똑한 z 샘플링 방식이 필요하다.

또한 z, $p(x,z)$ 가 거의 0이라 의미있는 샘플을 못뽑는다.

Importance Sampling

$$p_\theta(x) = \sum_{z \in \mathcal{Z}} p_\theta(x, z) = \sum_{z \in \mathcal{Z}} \frac{q(z)}{q(z)} p_\theta(x, z) = \mathbb{E_{z \sim q(z)}} \left[ \frac{p_\theta(x, z)}{q(z)} \right]$$

위 한계를 극복하기 위해 Important Sampling 방법을 도입한다. 위의 방법에서는 의미있는 z를 추출하지 못하므로 더욱 의미 있는 z를 더 자주 뽑는 분포 $q(z)$를 두는 방법을 사용한다.

참고로, 기대값의 정의는 다음과 같다.
$\mathbb{E_{z \sim q(z)}} [f(z)] = \sum_{z \in \mathcal{Z}} q(z) \cdot f(z)$

$$p_\theta(x) \approx \frac{1}{k} \sum_{j=1}^{k} \frac{p_\theta(x, z^{(j)})}{q(z^{(j)})} \quad \text{where } z^{(j)} \sim q(z)$$

기대값의 식이 나왔기 때문에 monte carlo를 사용할 수 있게 된다. 이때 z가 uniform 분포에 따른 것이 아니라 q의 분포에 따라 샘플링이 된다.

그렇다면 좋은 q의 분포가 무엇일까? 라는 의문이 생길 수 있다. $p_\theta(x,z)$ 가 z들을 자주 뽑는 분포가 좋은 q의 분포이다.

$$\mathbb{E_{z^{(j)} \sim q(z)}} \left[ \frac{1}{k} \sum_{j=1}^{k} \frac{p_\theta(x, z^{(j)})}{q(z^{(j)})} \right] = p_\theta(x)$$

또한 이는 unbiased estimator이다. Unbiased estimator는 추정한 값의 평균이 진짜 참값을 정확히 맞춘다는 뜻이다. (정답에 수렴한다.)

Monte carlo 실험을 아주 여러번 실행하면 결국 실제 값을 얻을 수 있게 된다.
해당 개념에 대한 정확한 내용은 이 사이트를 참고하면 좋을 것 같다.

Evidence Lower Bound(ELBO) - 1

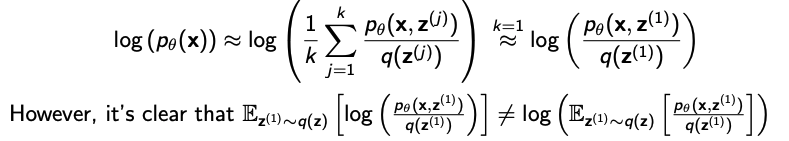
훈련 시, 우리가 관심이 있는 것은 데이터 포인트의 log-likelihood를 최적화 하는 것이다. 그래서 $p_\theta(x)$ 에 log를 씌우려고 봤더니 Jensen Inequality 때문에 로그 안에 샘플을 하나만 넣으면 편향이 생긴다. 위 그림의 2번째 줄의 수식들은 Monte carlo 식을 기대값으로 표현한 것이다.

23번 수식을 다시 보면, 각 data point들에 대한 marginal-log를 구하는 것을 확인할 수 있다.
로그의 특성(로그는 오목(concave)함수다.)상 샘플 평균에 로그를 씌우면 값이 크게 나오고, 로그 후 샘플 평균을 취하면 작게 나온다.

위 그림은 Jensen Inequality를 설명한 것이다. 선형결합을 한 것이 log 함수 값보다 훨씬 낮다는 것을 알 수 있다.

이 성질을 활용하여 다시 위 사진의 수식에서 $f(\mathbf{z}) = \frac{p_\theta(\mathbf{x}, \mathbf{z})}{q(\mathbf{z})}$ 를 넣어보면 아래와 같은 식으로 정리를 할 수 있다.

$$\log \left( \mathbb{E_{\mathbf{z} \sim q(\mathbf{z})}} \left[ \frac{p_\theta(\mathbf{x}, \mathbf{z})}{q(\mathbf{z})} \right] \right) \geq \mathbb{E_{\mathbf{z} \sim q(\mathbf{z})}} \left[ \log \left( \frac{p_\theta(\mathbf{x}, \mathbf{z})}{q(\mathbf{z})} \right) \right]$$

오른쪽 항을 이렇게 되면 우리가 원하는 객체에 대한 하한이 생긴다. 이를 Evidence Lower Bound(ELBO)라고 부른다.

오른쪽을 최적화 하면, 왼쪽도 희망적으로 증가할 것을 의미한다.
x가 evidence, x는 관찰된 부분이라는 뜻이다.

왼쪽을 최적화를 하진 못한다. 왜냐하면 왼쪽 항은 기대값을 먼저 계산 후, 그 결과에 로그를 취하는 형태이다. 하지만 기대값은 결국 28번 수식과 같이 통으로 $p_\theta(x)$ 로 나타낼 수 있기 때문에 결국 계산이 불가능하다는 것을 알 수 있다.

하지만 ELBO는 로그를 계산 후, 그 결과에 기대값을 취하는 형태이다. 따라서 이건 샘플링 기반으로 근사가 가능하다.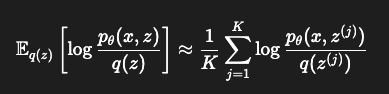

위 그림처럼 monte carlo를 사용할 수 있다.
그 후 $z^{(j)} \sim q(z)$ 여러개 샘플링하여 각각에 대해 log 값을 계산하고, 그것을 평균내면 된다.

따라서 ELBO를 활용하여 식을 전개하면 아래와 같다. 등호는 $q = p(z \mid x; \theta)$ 일때만 성립한다. 이에 대한 자세한 내용은 다음 강의에서 이어서 하겠다.

$$ \begin{aligned} \log p(x; \theta) &\geq \sum_{z} q(z) \log \left( \frac{p_\theta(x, z)}{q(z)} \right) \\ &= \sum_{z} q(z) \log p_\theta(x, z) - \sum_{z} q(z) \log q(z) \\ &= \sum_{z} q(z) \log p_\theta(x, z) + H(q) \ \text{(H(q) is entropy)} \\ \end{aligned} $$ $$ \begin{aligned} &\text{Equality holds if } q = p(z \mid x; \theta)\\ &\log p(x; \theta) = \sum_{z} q(z) \log p(z, x; \theta) + H(q) \end{aligned} $$