[CS236] 2. Background

GoodYoung included in DL Theory Lecture Deep Generative Models

2025-04-20 1262 words 6 minutes

Contents

개요

CS236: Deep Generative Models (Stanford)는 스탠포드 대학교에서 진행하는 딥러닝 기반 생성 모델(Deep Generative Models) 에 대한 심화 강의이다.

이번 포스트에서는 CS236 강의의 2강 내용을 정리한다.

2강에서는 말그대로 Generative 분야를 공부하기 전에 필요한 배경 지식을 설명하고 있다.

조건부 독립 (conditional independence)
generative model vs discriminative model

생성 모델이란 주어진 데이터(x)의 확률 분포(p(x))를 학습하여 샘플링하여 유사한 데이터를 생성해내는 것이다. ($x ~ p(x)$)

이런 확률 분포 p(x)에 대하여 여러 활용을 할 수 있는데, 아래는 그 활용에 대해서 나타낸다.
- 밀도 추정: 데이터 유사도 기반 이상 탐지 (원하는 object엔 p(x)가 높다.)
- Unsupervised representation learning: 공통된 특징 추출

그럼 이제 이러한 데이터의 확률분포 p(x)를 어떻게 표현을 할 것이냐가 먼저이다.

Representation p(x)

확률 분포의 표현은 여러가지이다. 베르누이 분포와 범주형(categorical)분포는 위 사진과 같이 표현할 수 있다.

만약 3개의 discrete random variable인 이미지 데이터라면, $p(R = r, G = g, B = b)$의 joint distribution을 구하기 위하여 $256 * 256 * 256 - 1$의 파라미터가 발생한다.

이때 말하는 파라미터란 무엇인가?
- 파라미터란 확률 분포를 정의하기 위해 필요한 개별 확률값을 의미한다.
- $X_1, X_2 \in {0, 1}$ 의 변수가 있다고 가정할 때 가능한 조합은 4가지 ((0,0), … (1,1))이다.
- 각 조합에 대해 확률 값을 지정해야 하지만, 전체 확률 합은 1이어야 하므로 4개 중 3개만 자유롭게 정하면 나머지 하나는 자동으로 정해진다.
  - 따라서 이 경우 $4 - 1 = 3$ 개의 파라미터를 가진다.

만약 n개의 binary(Bernoulli) random variable이라면 가능한 image의 수는 $2 \times 2 \times … \times 2 = 2^n$ (n: pixel 수)일 것이다.

그럼 이때 이 분포에서 sampling을 한다면 특정 분포의 joint distribution $p(x_1,…,x_n)$은 $2^n - 1$의 파라미터가 필요하다.

따라서 random variable의 수에 따라 파라미터의 수가 기하급수적으로 증가한다는 사실을 알 수 있다. 이 모든 값들을 컴퓨터에 저장하기엔 무리가 있다.

그렇기 때문에 수학적 가정이 필요한 순간이다. 그래서 독립성 가정(Independence Assumption)을 하겠다. $X_1, … , X_n$ 베르누이 분포를 만족하는 확률 변수들이 있다고 가정했을 때 $p(x_1, … , x_n) = p(x_1)\dot\dot\dot p(x_n)$ 을 만족한다.

이 경우, 가능한 상태(이미지)는 동일하게 $2^n$이고 joint distribution의 파라미터는 $n$이다.

Marginal distribution $p(x_1)$의 파라미터가 1이다.
따라서 $1 + 1 + … + 1$이기 때문에 파라미터는 n이 된다.

독립성 가정은 너무 strong해서 위의 그림 처럼 모든 값이 독립적으로 무작위 값을 선택하여 샘플링 결과가 안좋다.

$$p(S_1 \cap S_2 \cap \cdots \cap S_n) = p(S_1) \cdot p(S_2 \mid S_1) \cdot \cdots \cdot p(S_n \mid S_1 \cap \cdots \cap S_{n-1})$$ $$p(S_1 \mid S_2) = \frac{p(S_1 \cap S_2)}{p(S_2)} = \frac{p(S_2 \mid S_1) \cdot p(S_1)}{p(S_2)} $$

따라서 다른 가정이 필요하여 두가지 중요한 rule(공식)이 있다. 위는 순서대로 Chain rule (probability)와 Bayes' rule의 식이다.

$$p(x_1, x_2, \ldots, x_n) = p(x_1) \cdot p(x_2 \mid x_1) \cdot p(x_3 \mid x_1, x_2) \cdots p(x_n \mid x_1, \ldots, x_{n-1})$$

Chain Rule을 사용하면 위의 식이 된다. 이때 파라미터는 $1+2+…+2^\text{n-1} = 2^n - 1$이다.

여전히 exponential하다는 것을 알 수 있다. 이 chain rule을 사용한 식에 conditional independence를 가정을 한다.

$$p(x_1, x_2, \ldots, x_n) = p(x_1) \cdot p(x_2 \mid x_1) \cdot p(x_3 \mid x_2) \cdots p(x_n \mid x_{n-1})$$

그렇게 되면 위의 식과 같아지고 파라미터는 $2n - 1$로 해결이 가능해졌다. ($X_{i+1} \perp {X_1, \ldots, X_{i-1}} \mid X_i$ 이렇게도 표기한다.)

Bayes Network

Chain rule을 통해 모든 확률변수의 joint distribution을 표현할 수 있지만, 이때 conditional independence를 활용하면 필요한 파라미터 수를 대폭 줄일 수 있다. 베이지안 네트워크는 이러한 조건부 독립 구조를 그래프 형태로 표현한 모델이다.

베이지안 네트워크는 각 확률 변수마다 노드를 가진다.
노드 간 관계는 부모 자식 구조($\text{Pa}(i)$)로 표현이 된다.
각 노드마다 부모 노드의 값에 조건부 형태로 표현을 할 수 있고 전체 분포는 아래 식과 같다.
$p(x_1, x_2, \ldots, x_n) = \prod_{i \in V} p(x_i \mid x_{\text{Pa}(i)})$

Conditional Independence를 기반으로 복잡한 분포를 단순하게 표현을 하여 조합 수가 많은 경우에도, 각 노드의 부모 수만큼만 파라미터가 필요하여 효율적이다.

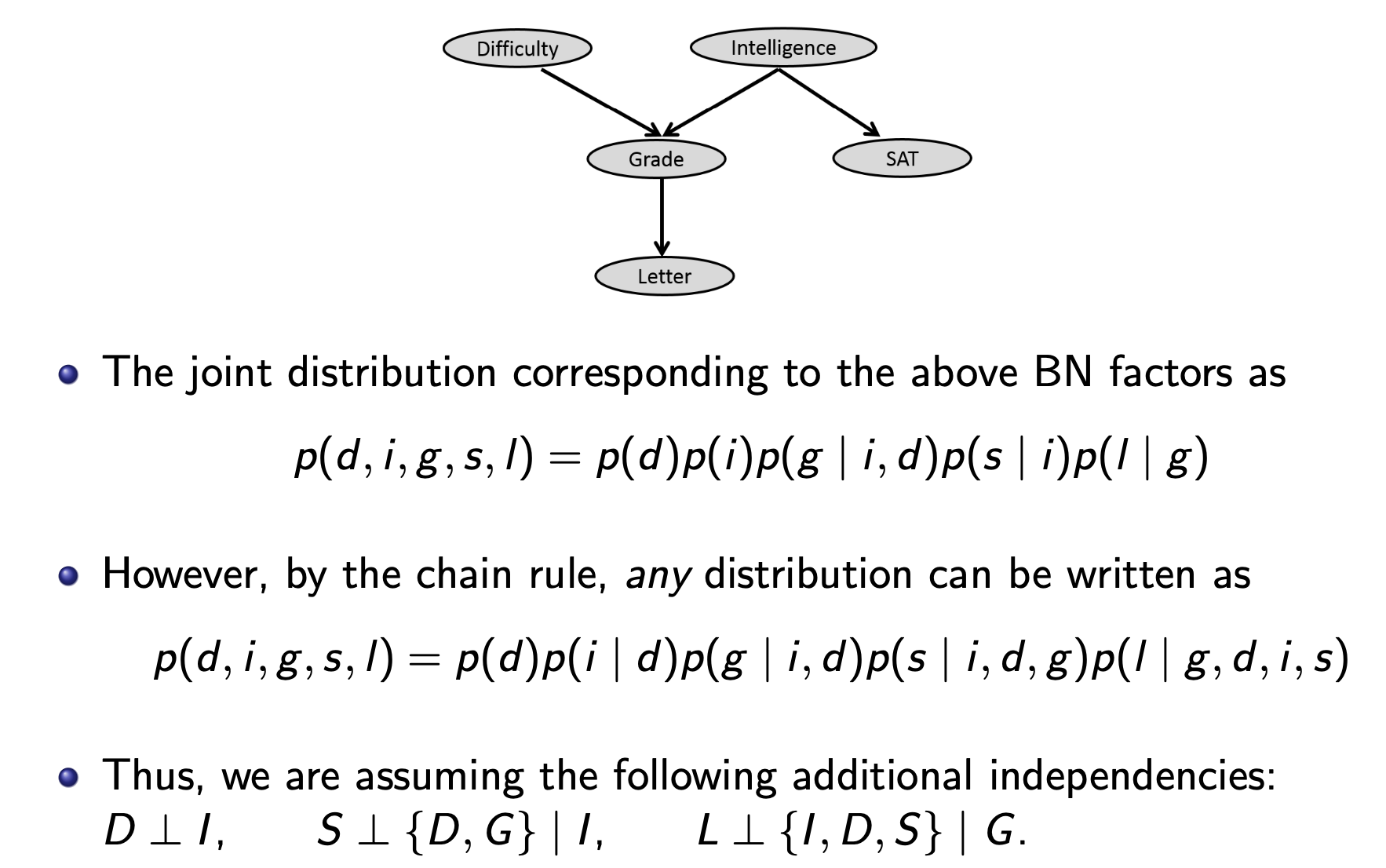
위 그림을 보면 그래프를 베이지안 네트워크로 표현을 할 수 있고, 독립성들을 파악하기 쉽다.

최종 정리를 하자면 베이지안 네트워크는 확률 변수들 간의 조건부 독립성을 방향 그래프(DAG)로 표현한 모델이다.

Naive Bayes

$$p(y, x_1, \ldots, x_n) = p(y) \prod_{i=1}^{n} p(x_i \mid y)$$

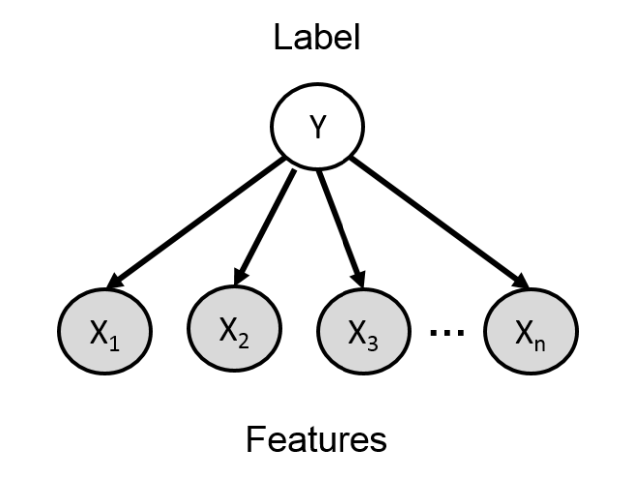
이메일이 스팸인지 여부(y) 를 판단할 때, Naive Bayes를 사용하여 분류를 진행한다. 이때 이 방법은 가정이 있게되는데 바로 단어들이 클래스 $Y$가 주어졌을 때 조건부 독립이라고 가정한다. 이 가정을 활용한 식은 위 식과 같다.

나이브 베이즈 분류기는 학습 시 각 조건부 확률 $p(X_i | Y)$와 클래스 분포 $p(Y)$를 학습한다. 그리고 추론 시 $p(Y = 1 | X)$를 계산하면 된다. 추론 시 베이즈 정리를 적용 하면 아래 식과 같아지게 된다.

이 나이브 베이즈 분류기는 완벽하지 않지만, 유용할 수 있다.
나이브 베이즈 분류기는 베이지안 네트워크의 아주 단순화된 형태라고 생각하면 될 것 같다.

$$p(Y = 1 \mid x_1, \ldots, x_n) = \frac{ p(Y = 1) \prod_{i=1}^{n} p(x_i \mid Y = 1) }{ \sum\limits_{y \in {0,1}} p(Y = y) \prod_{i=1}^{n} p(x_i \mid Y = y) }$$

Generative & Discriminative Model

생성 모델과 판별 모델을 노드로 관계를 나타낸 것이다. 생성 모델은 x,y사이의 전체 관계($p(x,y) = p(x|y)p(y)$)를나타내고 판별 모델은 주어진 x에 대해 y를 바로 예측($p(y|x)$)을 한다.

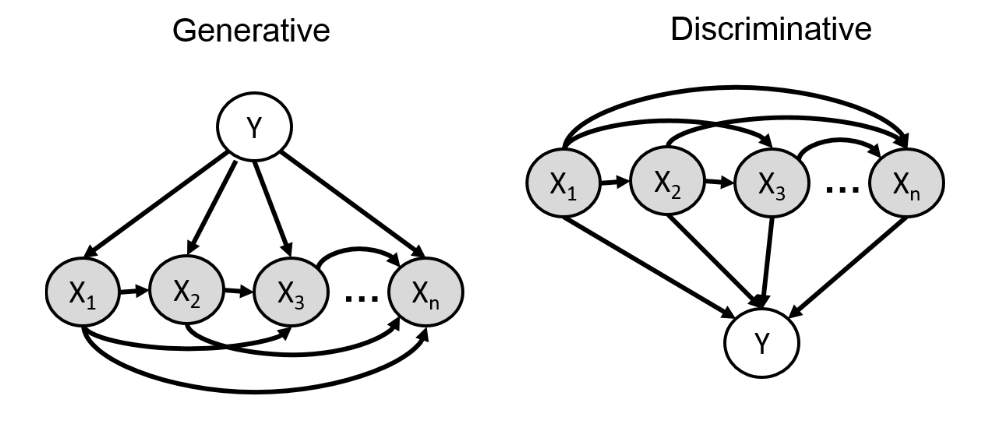
따라서 생성 모델은 모든 조건부 분포를 다 배울 필요가 있지만 판별 모델은 분류만 하므로 x의 분포를 신경을 안써도 된다.

따라서 이런 생성 모델의 복잡한 관계를 naive Bayes 가정을 활용하여 단순하게 만들 수 있게 된다.

위 그림을 보면 y를 알면 x를 알 수 있게 된다.

이런 나이브 베이즈를 사용한 모델은 가정으로 인하여 X들간의 상관관계는 무시되기 때문에 $X_1$과 $X_2$가 y와 항상 같이 나온다면 $X_1$과 $X_2$가 실제로 각각 유의미해도 $p(X_1|Y) = p(X_2|Y) $ 으로 처리한다.

하지만 판별 모델 중 하나인 로지스틱 회귀는 각 특성의 기여도를 조정할 수 있어 이런 중복 문제를 해결할 수 있다.

로지스틱 회귀란 Linear Regression에 로지스틱 함수를 적용한 모델이다. 아래는 관련 식이다.
$z(\alpha, x) = \alpha_0 + \sum_{i=1}^{n} \alpha_i x_i$ 의 선형 결합으로 나타낼 수 있다.
$p(Y = 1 \mid x; \alpha) = \sigma(z(\alpha, x)) = \frac{1}{1 + e^{-z(\alpha, x)}}$ 으로 확률로 변경할 수 있다.
이 같은 식을 통하여 decision boundary를 정할 수 있게 된다.

이런 생성 모델도 장점이 있는데 바로 X의 일부 값이 관측되지 않았을 때도 추론이 가능하다는 점이다.

Neural Models

$$h(A, b, x) = f(Ax + b)$$ $$p_{\text{Neural}}(Y = 1 \mid x; \alpha, A, b) = \sigma\left( \alpha_0 + \sum_{i=1}^{h} \alpha_i h_i \right)$$ 28. 기존 로지스틱 회귀는 선형 관계라 구조가 단순하다. 따라서 비선형 모델링(Neural Network)이 필요해졌다. 따라서 위의 식과 같이 표현이 가능하고 기존보다 더 다양한 파라미터가 생긴 것을 확인 할 수 있다.

따라서 지금까지의 모델들을 정리를 해보면 아래와 같다.

Chain Rule 공식
- $p(x_1, x_2, x_3, x_4) = p(x_1) \cdot p(x_2 \mid x_1) \cdot p(x_3 \mid x_1, x_2) \cdot p(x_4 \mid x_1, x_2, x_3)$
Bayesian Network (assumes conditional independency)
- $p(x_1, x_2, x_3, x_4) \approx p(x_1) \cdot p(x_2 \mid x_1) \cdot p(x_3 \mid \cancel{x_1}, x_2) \cdot p(x_4 \mid \cancel{x_1}, \cancel{x_2}, x_3)$
Neural Models
- $p(x_1, x_2, x_3, x_4) \approx p(x_1) \cdot p(x_2 \mid x_1) \cdot p_{\text{Neural}}(x_3 \mid x_1, x_2) \cdot p_{\text{Neural}}(x_4 \mid x_1, x_2, x_3)$

Continuous Variable

$X$가 연속확률변수일 때는 지금까지 배운 방법을 어떻게 적용시키는 지에 대하여 나온다.

바로 Probability Density Function (PDF)를 사용하여 모델링을 하고 Chain rule, Bayes rule에 똑같이 조건부 확률 형태를 적용하면 된다.

이때 모델링 시 사용되는 분포가 있다.
- 정규 분포, 다변량 정규 분포 등이 있다.
정규분포와 같은 분포에서는 각 점에서의 확률이 아니라 확률 밀도 $p(x)$가 주어지고, 우리가 원하는 실제 확률은 이 밀도 값을 구간에 대해 적분해서 얻는다.

그럼 이런 연속확률변수를 사용하여 어떻게 Bayesian network를 활용한 모델이 구성될 수 있는지에 대한 예제를 설명할 것이다.

이제 설명하는 모델들은 $Z$-> $X$ 의 관계를 $p(Z, X) = p(Z) \cdot p(X \mid Z)$ 으로 **분해(factorization)**가 가능한 Bayesian network라고 생각하면 된다.

아래 세개의 모델들은 다음과 같은 순서로 진행되고 그 순서에서 안에 구성만이 다른 것이다.
1. z가 어떤 분포에서 샘플링이 된다.
2. 그 z의 값으로 정규분포가 정해진다. 그리고 그 정규분포에서 X를 샘플링을 한다.

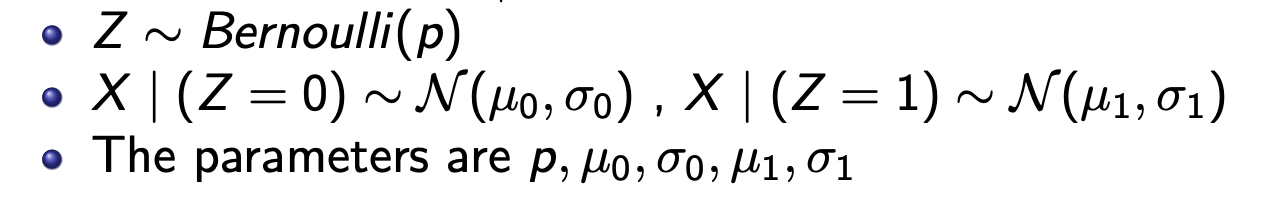
첫번째 모델은 Mixture of 2 Gaussian이다. 베르누이 분포에서 뽑은(2가지 경우) z에 해당하는 분포에서 X를 샘플링을 한다.

z는 어떤 분포($\mu_0, \mu_1)$에서 샘플링(X)을 할 지 알려준다.

두번째 모델은 uniform 분포에서 뽑아서 뽑은 z를 중심으로 아주 약간 움직인 분포로 구성할 수 있다.

세번째 모델은 정규분포의 평균과 분산이 신경망으로부터 결정이 된 분포에서 샘플링이 된다.

신경망 기반 조건부 확률 분포이다.

결론적으로 베이지안 네트워크는 다양한 생성 모델(Gaussian mixture, VAE 등)을 구조적으로 설명하고 일반화 할 수 있다.