[CS231n] 09.CNN Architectures
Contents
개요
CS231n의 9강에 대한 내용을 정리 할 것이다.
- 9강에 나오는
CNN Architecture중에GoogLeNet과ResNet에 대해서 살펴볼 예정이다.
GoogLeNet
- 이때부터 이제
Network를 깊게 효율적을 만들기 시작했다.
Network가 깊어질수록 학습하는데 걸리는 컴퓨팅 시간이 많이 걸린다. 따라서Network를 깊고 효율적으로 만들기 위해서GoogLeNet에서는Inception module을 추가하였다.
-
Inception Module이란 로컬 네트워크의 한 유형이다. 이는 네트워크의 네트워크 (Network In Network(NiN))의 개념에 바탕을 두고 있다.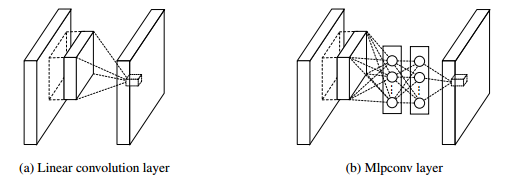
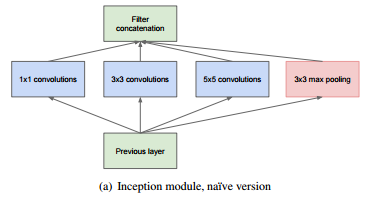
Inception Module은위 그림과 같이 병렬로 서로 다른 크기의 filter를 병렬로 돌려 차원을 줄여주는 것이다.
- 서로 다른 크기의 filter가 있으므로 여러 특징을 추출하는 효과를 가진다.
- 위 그림은
naive Inception module이다. Filter들의stride와padding을 통하여 입력과 출력 차원을 일치시키고 depth를 높였다.
- 이 module의 문제는
computational complexity이다.- Pooling layer가 depth를 유지하기 때문에 every layer에서 전체적인 depth가 깊어진다.
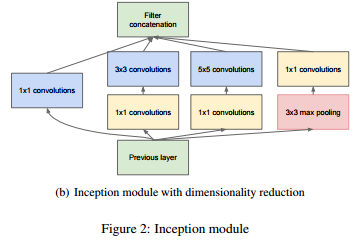
- 이를 해결하려고
boottleneck layer가 나온다.- 33, 55 filter에 들어가기 전 1*1 filter를 사용하여 depth를 줄인다.
- 따라서 기존과 확연히 다른 연산을 수행하는 것을 확인할 수 있게 된다.
- 1*1 를 사용하면 정보 손실이 발생할 수 있지만 이러한 예측을 수행하는 경우 이들의 조합을 계산하여 추가적으로 비선형성을 도입하므로 이를 보완할 수 있다.
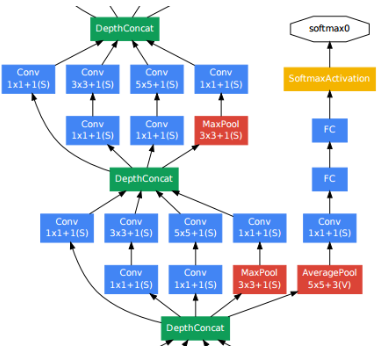
- 또한
GoogLeNet에서는auxiliary classification output이 있다.- To inject additional gradient at lower layers
Gradient가 잘 전달이 되지 않는 깊은Network에서 중간 layer도 도움이 된다.- 깊은 네트워크 때문에
gradient vanishing현상을 극복하려고 inject를 한다.
- To inject additional gradient at lower layers
- 이는 메인 네트워크의 최종 손실과 함께 결합되어 최종 학습 과정에 기여하게 된다.
ResNet
- 다음은 2015년에
ILSVRC에서 우승을 한ResNet이다. 이는revolution of Depth인 만큼 많이 깊은 network이다.
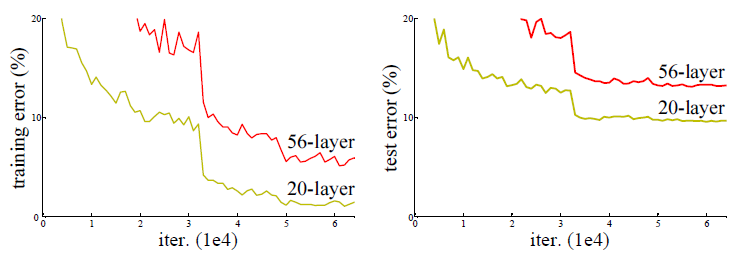
- 엄청 깊게
CNN을 쌓으면 더 나은 결과가 나오나 싶지만 결과는 아니였다.
- Train시
overfitting이 예상이 되어 오류가 아주 적을 것이라 예상을 했지만 그것의 문제가 아니다.- 이는 모델 자체는 학습이 이뤄지고 있어서
vanishing gradient문제가 아닌degradation problem이다.
- 이는 모델 자체는 학습이 이뤄지고 있어서
- 이는
optimization problem이다. 적어도 깊은 layer는 shallower의 성능은 기본적으로 있어야 하지만 그 조차도 아니다.- 깊은 layer는 shallower model보다 최적화 하기 어렵다.
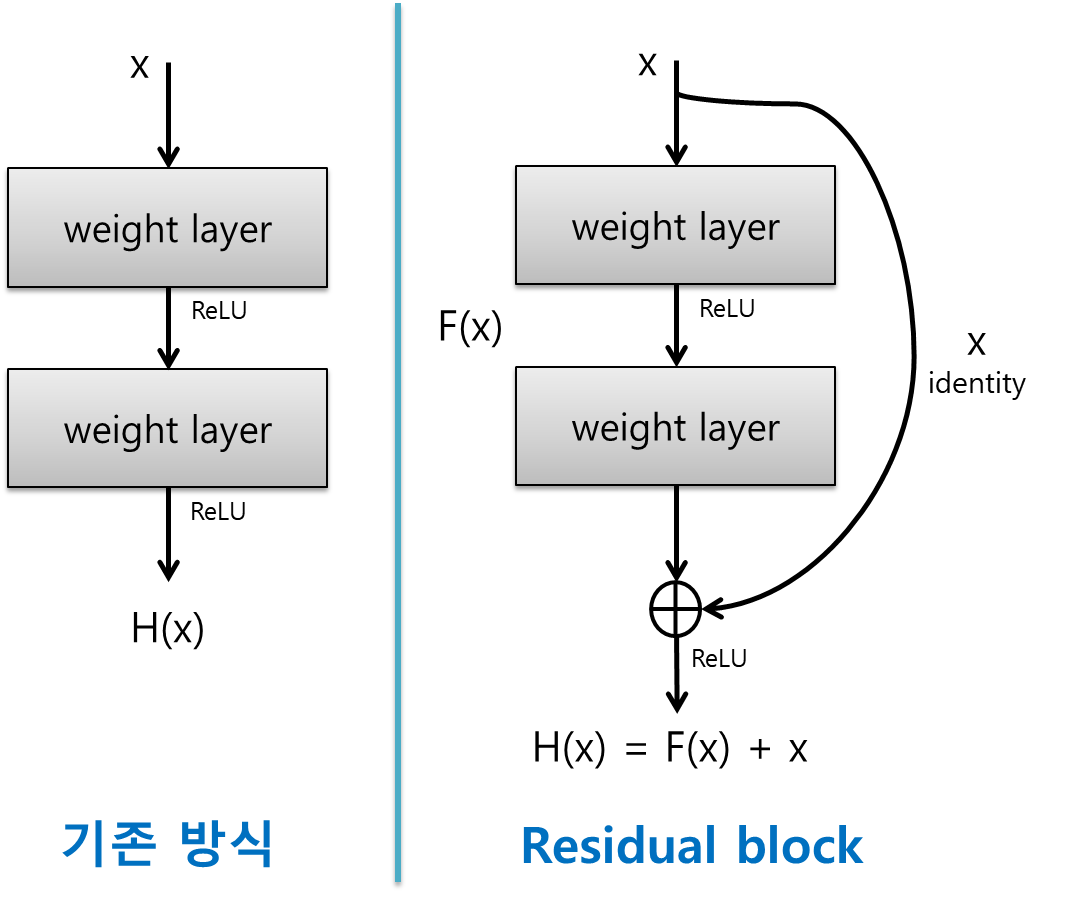
- 이걸 해결하려고
residual connection이 나왔다.
- 이는 아주 간단하게 입력을 출력에 더하는 아이디어 이런 단순한 아이디어 이다.
- 모델이 학습을 할 때 $H(x)$를 하는 것이 아니라 x를 뺀 나머지(잔차 $F(x)$)를 학습을 하게 된다.
- 이를 더 자세히 이해하자면 학습이 많이 될수록 x는 점점 출력값 $H(x)$에 근접하게 된다.
- 이
residual connection에서는 x가identity mapping이 되기 때문에 $H(x) = F(x) + x$에서 추가 학습량 F(x)는 점점 작아져서 최종적으로 0에 근접하는 최소값으로 수렴되어야 할 것이다.
- 이렇기 때문에 함수 전체를 학습하는 대신, 더 단순한 잔차만 학습하게 되므로
residual connection은 학습 과정이 더 빠르고 쉽고 깊은 네트워크에서 안정적이다.
- 이를 수식적인 이해를 한다면 아래와 같다.
Residual connection이 있는 신경망에서 아래 같이 표현을 할 수 있다.
$$y = F(x) + x$$
-
기본 신경망에서는 손실 함수 $L$은 체인 룰을 통해 gradient update를 하게 된다. $$\frac{\partial L}{\partial x} = \frac{\partial L}{\partial y} \cdot \frac{\partial y}{\partial x}$$
-
Residual connection이 있을 때 기울기 전파는 아래와 같다.
$$y = F(x) + x$$
$$\frac{\partial y} {\partial x} = \frac{\partial (F(x) + x)}{\partial x}$$
- $\frac{\partial x}{\partial x} = 1$ 이므로 다음과 같이 표현할 수 있다.
$$\frac{\partial y}{\partial x} = \frac{\partial F(x)}{\partial x} + 1$$
- 결국,
gradient전파는 다음과 같이 계산이 된다.
$$\frac{\partial L}{\partial x} = \frac{\partial L}{\partial y} \cdot (\frac{\partial F(x)}{\partial x} + 1)$$
Residual connection이 없는 경우, $(\frac{\partial F(x)}{\partial x})$가 매우 작아지면 기울기 소실 문제가 발생할 수 있다.
- 하지만,
Residual connection이 있는 경우, $(\frac{\partial F(x)}{\partial x} + 1)$의 형태로 계산되므로, $(\frac{\partial F(x)}{\partial x})$가 0에 가까워지더라도, 항상 1이 더해지기 때문에 기울기가 완전히 사라지지 않게 되어vanishing gradient현상도 해결이 될 수 있다.
- 즉,
Residual connection을 통해 기울기가 더 안정적으로 전파될 수 있으며, 이는 깊은 신경망에서도 학습이 잘 이루어지도록 도와주게 된다.