[CS231n] 06.Training Neural Networks I

GoodYoung included in DL Theory Lecture

2024-07-18 1566 words 8 minutes

Contents

개요

CS231n의 6강에 대한 내용을 정리 할 것이다.

저번 강에서는 Convolutional Neural Networks에 대해 배웠고 이번 강에서는 이 Neural Networks를 어떻게 하면 잘 학습시킬 수 있을지에 대해서 배울 것이다.

Activation Function

Deep Network에 비선형성을 부여하는 Activation Function의 종류들에 대해서 알아볼 것이다.

Sigmoid

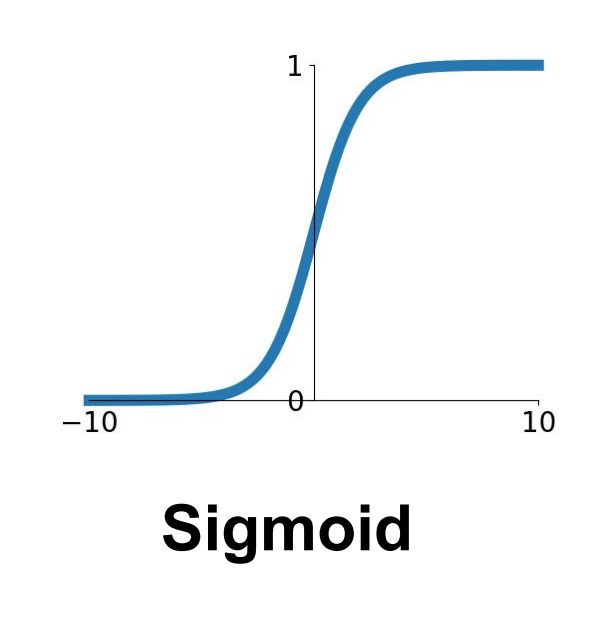
$$\sigma(x) = \frac{1}{1 + e^{-x}}$$

먼저 첫 번째로 Sigmoid이다. 함수의 모양은 위 그림과 같고 (0,1) 사이의 값을 가지게 된다.Sigmoid가 가지게 되는 몇가지 문제들이 있다.

첫 번째 문제는 경사도를 죽일 수 있는 문제이다.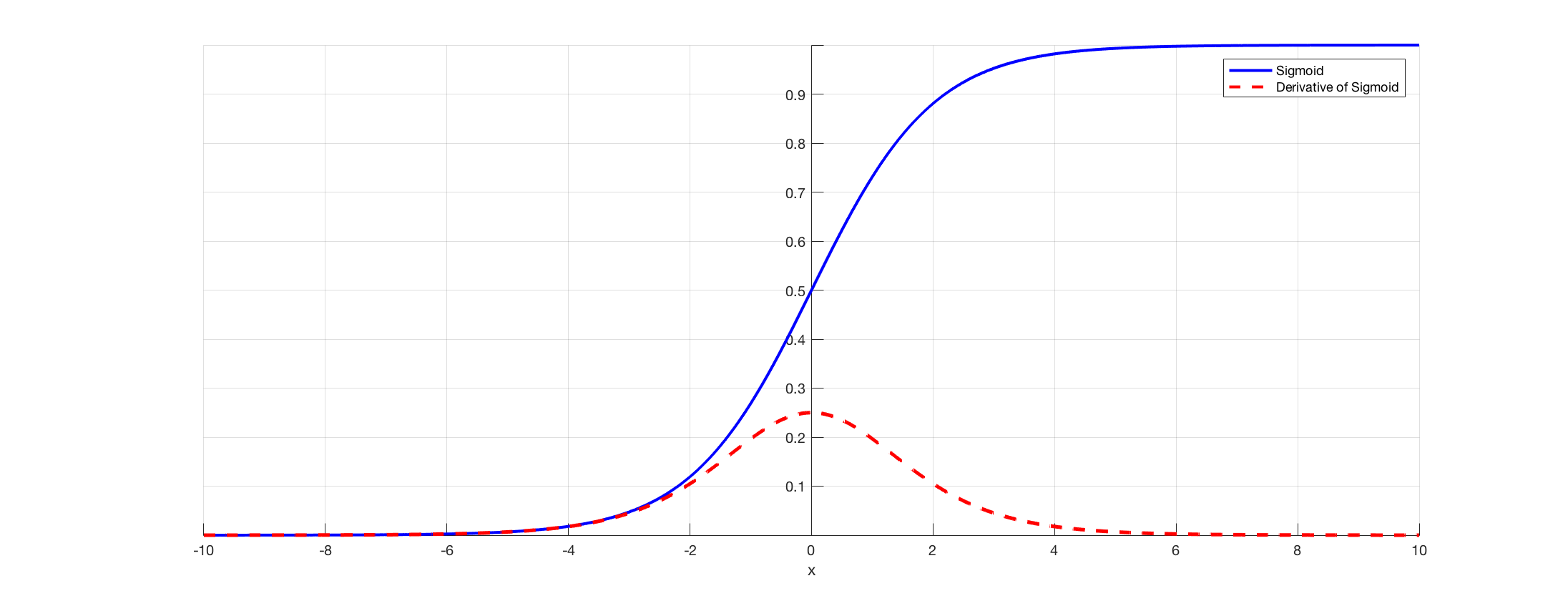

이는 입력으로 들어오는 x가 -10, 10이라면 global gradient(이전 노드의 기울기)는 0이 되고 이것이 역전파를 통해 다운스트림($global grdient * local gradient$) 되면 global gradient가 0이므로 아래 노드들은 0으로 수렴하게 되어 기울기가 소실이 된다.
- 이러한 기울기 소실로 인하여 W의 값을 더이상 update 하지 못하는 문제를 vanishing gradient라고 한다.

두 번째 문제는 output이 zero-center가 아닌 문제이다. 즉, Signmoid의 output이 항상 양수이기 때문에 0을 중심으로 있지 않는 문제가 발생하게 된다.

ouput이 항상 양수 이라면 입력값 또한 양수인 것인데, 그렇게 된다면 back propagation에서 $\frac{dl}{df} * \frac{df}{wi}$ 로 W의 기울기를 chain-rule로 구하게 된다.

근데 우리가 이전 4강에서 배운 chain-rule의 pattern 중 mul gate(곱)일 때 grdient가 서로 전환이 된다고 배웠다. 따라서 $\frac{df}{wi}$ 이것이 바로 $x_i$인 것을 알 수 있게 된다.
- 이때 $x_i$가 이전 layer의 sigmoid 연산을 거친 output이기 때문에 무조건 양수이다.

입력값은 항상 양수라면 back propagation을 할 때 $\frac{dl}{df}$(global gradient이다.)의 부호를 따라가게 되어서 gradient의 부호는 항상 양수이거나 음수가 된다.
- 부가적으로 gradient의 부호는 다운 스트림으로 내려온 gradient의 부호와 같아진다고 생각하면 쉽다.

이렇게 부호가 모두 양수 또는 음수가 되어버리면 발생하는 문제는 gradient update를 할 때 나타난다.

w1,w2가 있다면 gradient update시 항상 (+)(+) 이거나 (-)(-)가 된다. 따라서 위 그림과 같이 파란색 방향(최적의 gradient update)과는 다르게 비효율적으로 지그재그 방향으로 내려가게 되는 상황이 벌어지게 된다.

이를 해결할 수 있는 방법은 input값에 mean을 모두 빼버리면 zero-mean data가 된다. 그렇게 되면 X가 양수/음수를 모두 가지고 있는 상황을 만들 수 있게 된다.

마지막 세 번째 문제는 Sigmoid에서의 exp의 연산의 계산 비용이 많이 들어간다는 것이다.
- 따라서 위 세 가지의 문제로 잘 사용하지 않게 된다.

tanh

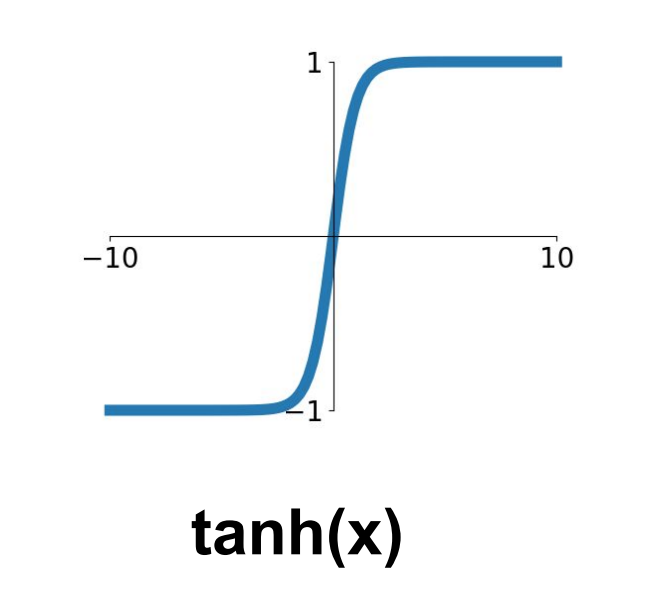
다음은 tanh함수이다. 이는 범위를 (-1,1)까지 하여 Sigmoid의 단점인 non-zero-center문제를 해결하게 되었다.

하지만 여전히 그래프를 봐도 확인 할 수 있지만 경사도를 죽일 수 있는 문제는 해결되지 못하였다. 따라서 Network가 깊어지는 모델이 많아진 요즘 활성화 함수로 잘 사용하지 않게 된다.

ReLU

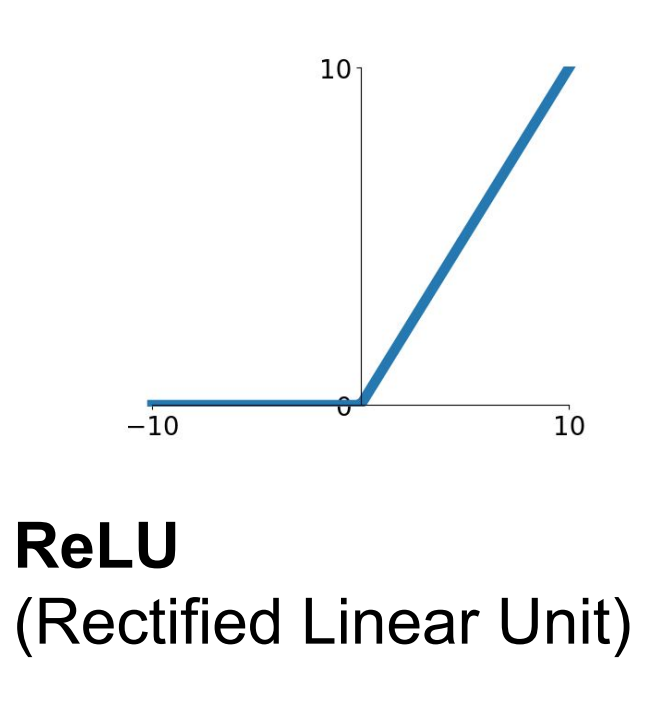
$$f(x) = max(0,x)$$

다음은 ReLU함수 이다. 이는 위 두 함수과 다르게 양수에서 경사도를 죽일 수 있는 문제를 해결 하였다.

또한 이 함수는 최대값만 계산하기 때문에 연산이 효율적이고 실제로 앞선 함수들과 비교하여 6배가 빠르다고 한다.

하지만 ReLU함수도 몇가지 문제점이 있다. Non-zero-center문제를 가지고 있고 또한 음수일 경우에는 경사도를 죽일 수 있는 문제가 발생할 수 있다.

따라서 W를 initialization하는 과정에서 잘못되었을 때 dead ReLU가 발생할 수 있다.
- 따라서 이런 dead ReLU를 피하기 위하여 초기화를 할 때 positive한 bias를 얻게 초기화를 하는 방법도 있지만 효과가 경미하다.

또한 learning rate를 크게 설정하는 대규모 훈련 시 W가 너무 크게 비약해서 학습이 안되는 상황이 발생할 수도 있다.

실제로 ReLU를 사용한 Network에서 10~20% 정도가 dead ReLU에 빠진다고 한다.
- 문제이긴 하지만 그럼에도 불구하고, train은 잘 된다고 한다.

Leaky ReLU

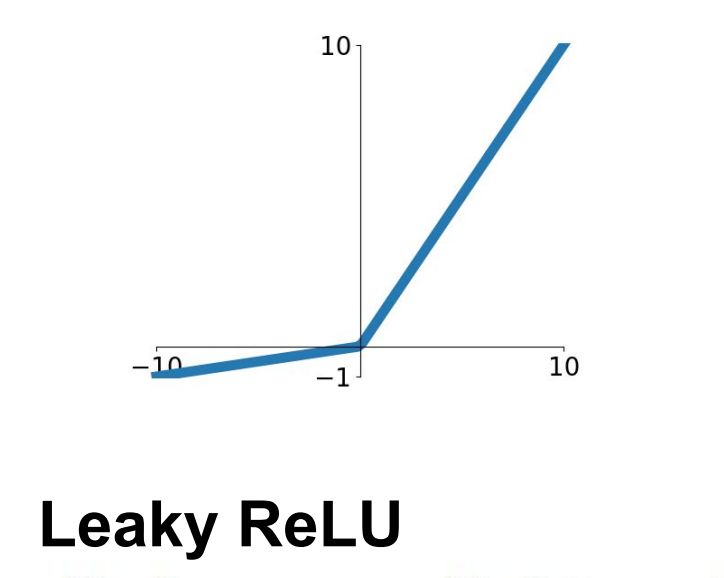
$$f(x) = max(0.01x,x)$$

ReLU와 다르게 음수에도 음수 기울기를 주어 경사도를 죽일 수 있는 문제를 해결하고자 한다.
- ReLU와 같게 연산이 빠르다는 장점도 있다.

PReLU

$$f(x) = max(ax,x)$$

PReLU는 음수 영역에 backpropagation에서의 파라미터로 기울기 값으로 유연성을 더해주어 조금 더 융통성을 가해 주었고

ELU

다음의 ELU는 평균 출력이 더욱 0에 가까워지게 만든 함수이다. 그래서 다음과 같은 장점이 있다.
- 노이즈에 더욱 견고해진다.
- Leaky ReLU와 비교했을 때 비활성화 상태를 더욱 robust하게 얻을 수 있다.

Maxout Neuron

$$\max(w_1^T x + b_1, w_2^T x + b_2)$$

다은은 Maxout Neuron이다. 파라미터를 더 두어서 두가지의 function의 max를 취하게 된다.
- 경사도를 죽일 수 있는 문제는 사라졌지만 뉴런 당 parameter가 2배로 증가하는 단점이 있다.

Data Preprocessing

다음은 좋은 데이터를 만들기 위한 data preprocessing과정에 대해 설명할 것이다.

일반적으로 image 데이터의 경우에는 zero-mean만 전처리를 수행한다.
- 입력값이 전부 양수이면 W가 한 방향으로만 업데이트가 일어나기 때문에 비효율적이다.
- 오직 첫 layer에서만 zero - centering이 되고, 그 이후에 네트워크가 깊어지면 깊어질수록 활성화 함수로 값이 양수만 나와서 첫 layer 정도에만 의미가 있다.

image의 경우에는 normalize를 많이 하지 않는다.
- 왜냐하면 image의 경우 각 위치에는 이미 상대적으로 규모와 분포가 있기 때문이다.
- 이미지는 픽셀 값이 전부 같은 범위(0~255)이기 때문이다.

또한 image의 경우 일부 작업(PCA, Whitening)을 하지 않는다.
- 일반적으로 원본 image 위에 convolution layer를 통하여 공간 구조를 포함한 특징 추출을 하기 때문이다.

Zero-mean의 전처리를 할 경우 훈련데이터에서 얻은 경험적인 image의 평균을 test데이터에서 그대로 사용한다.

이때 mean의 값을 이미지의 전체 데이터로 할지, 아니면 각각 독립된 채널마다의 mean으로 이용할 지 선택할 수 있는데, 이는 큰 차이는 나지 않는다고 한다.

Weight Initialization

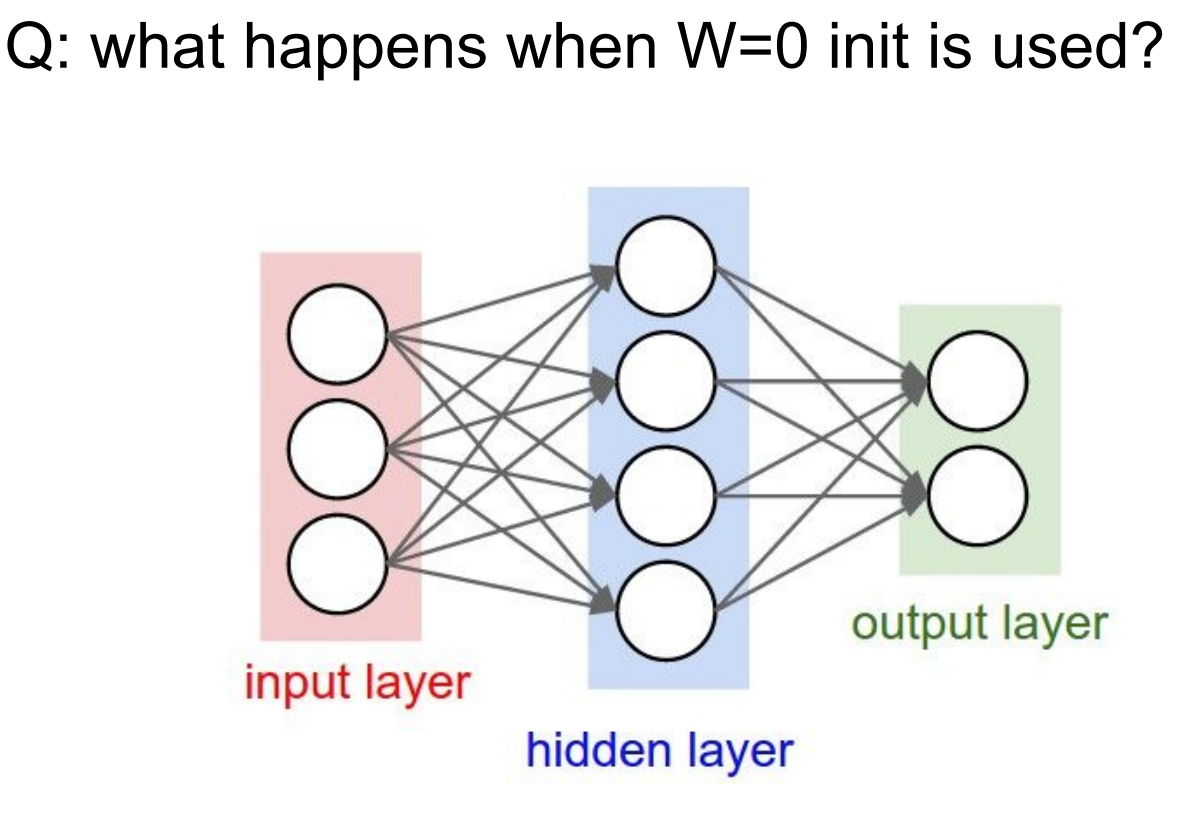
다음은 W를 초기화 하는 방법에 대해서 알아볼 것이다.

위 그림처럼 w가 0으로 초기화가 된다는 질문을 남긴다. 그렇게 되면 입력값에서부터 뉴런이 모두 동일한 결과를 내놓는다.

따라서 W를 초기화 시키는 여러 방법에 대해서 설명한다. 첫 번째 방법은 Small random number이다.
```
W = 0.01 * np.random.randn(D,H)
```

이 방법은 분포에서 샘플링을 할 수 있는 작은 난수로 설정하는 방법이다.
- 대칭성이 없어져서 small network에서는 잘 작동하지만 deep network에서는 문제이다.

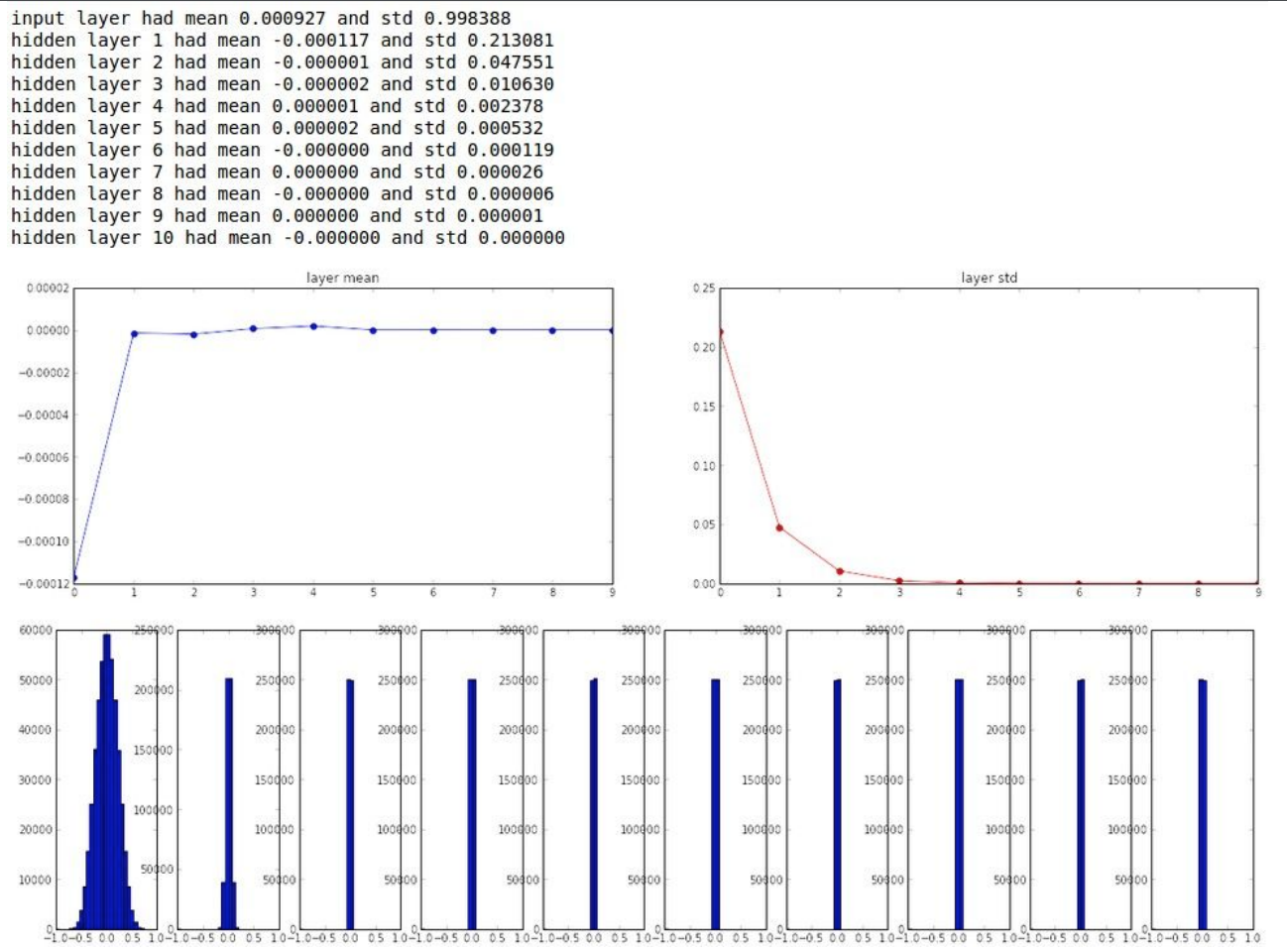
위 그림은 activation function으로 tanh, hidden layer 10개, 뉴런이 총 500개 인것을 Small random number의 방법을 사용하여 실험해본 결과를 각 layer마다 분포를 확인한 것이다.
- 그림의 윗 부분을 보면 tanh가 zero-center이기 때문에 layer를 지날 수록 mean이 0으로 나온다.
  - 표준편차는 0으로 붕괴된다.

그림의 아랫 부분을 보면 첫 layer에는 가우시안 분포를 띄지만 점점 무너지는 것을 확인할 수 있게 된다. 왜냐하면 각 layer에 작은 숫자를 곱하면($W*x$에서 W가 임의의 작은 수이므로 작은 수를 계속 곱하니까) 모든 값이 빠르게 줄어들고 무너지는 것을 확인할 수 있다.

또한 이때 back propagation을 할 때는 입력 값이 매우 작다. $W*X$ gate에서 W의 local gradient는 X이다. 따라서 X가 작기 때문에 가중치가 매우 작은 기울기를 얻고 업데이트되지 않는다.
- vanishing gradient 현상이 일어난다.

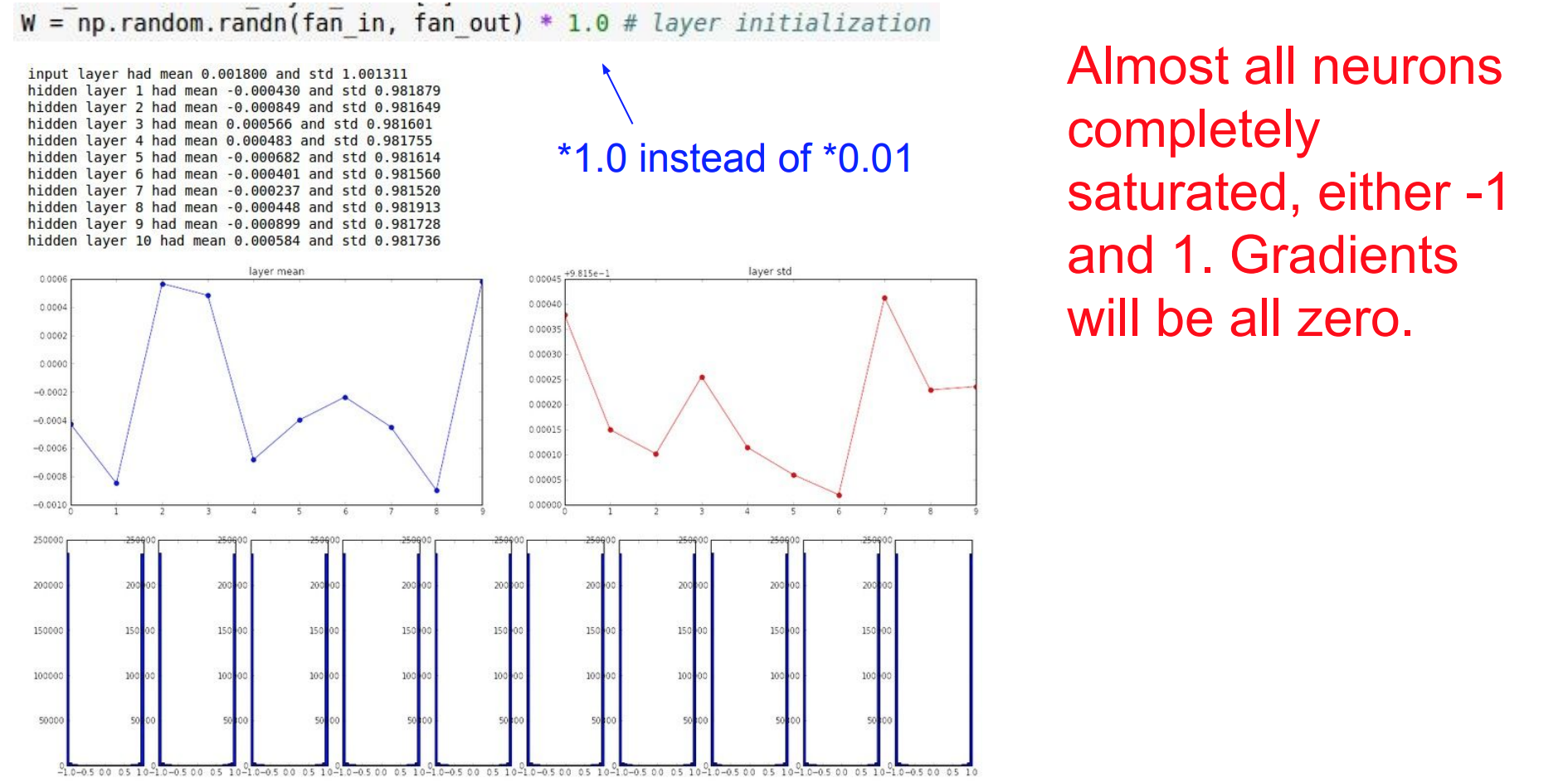
두 번째 방법은 W의 값을 반대로 크게 한다면?

W = 1 * np.random.randn(fan_in, fan_out) # input, output의 수

출력 값들이 1과 -1쪽으로만 가서 explode가 된다.
- 따라서 tanh에서 1,-1은 각각 기울기가 0인 지점이다. 따라서 gradient가 0이 되어 update가 되지 않는다.

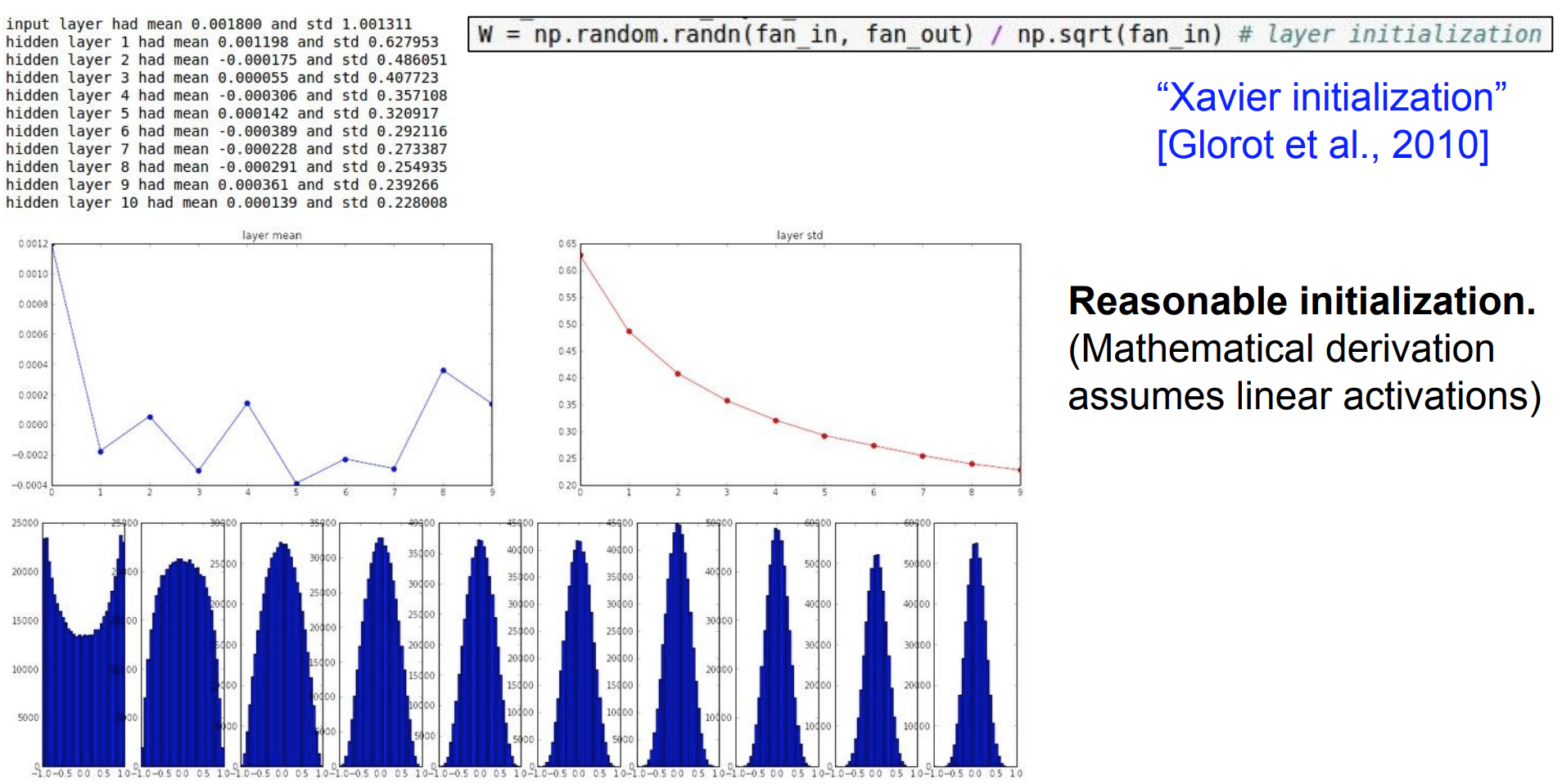
앞 선 두 방식 말고 W의 값을 입력의 수를 계산하여 입력 수를 np.sqrt로 나누어 스케일링을 해주는 방식이 있다. - 이는 작은 숫자면 작은 숫자로 나누고 더 큰 가중치를 얻으면 더 큰 가중치가 필요하다 - 즉, 상대적으로 입력값의 개수에 따라 값을 조절하여 초기화 하기 때문에 합리적인 방식이다.

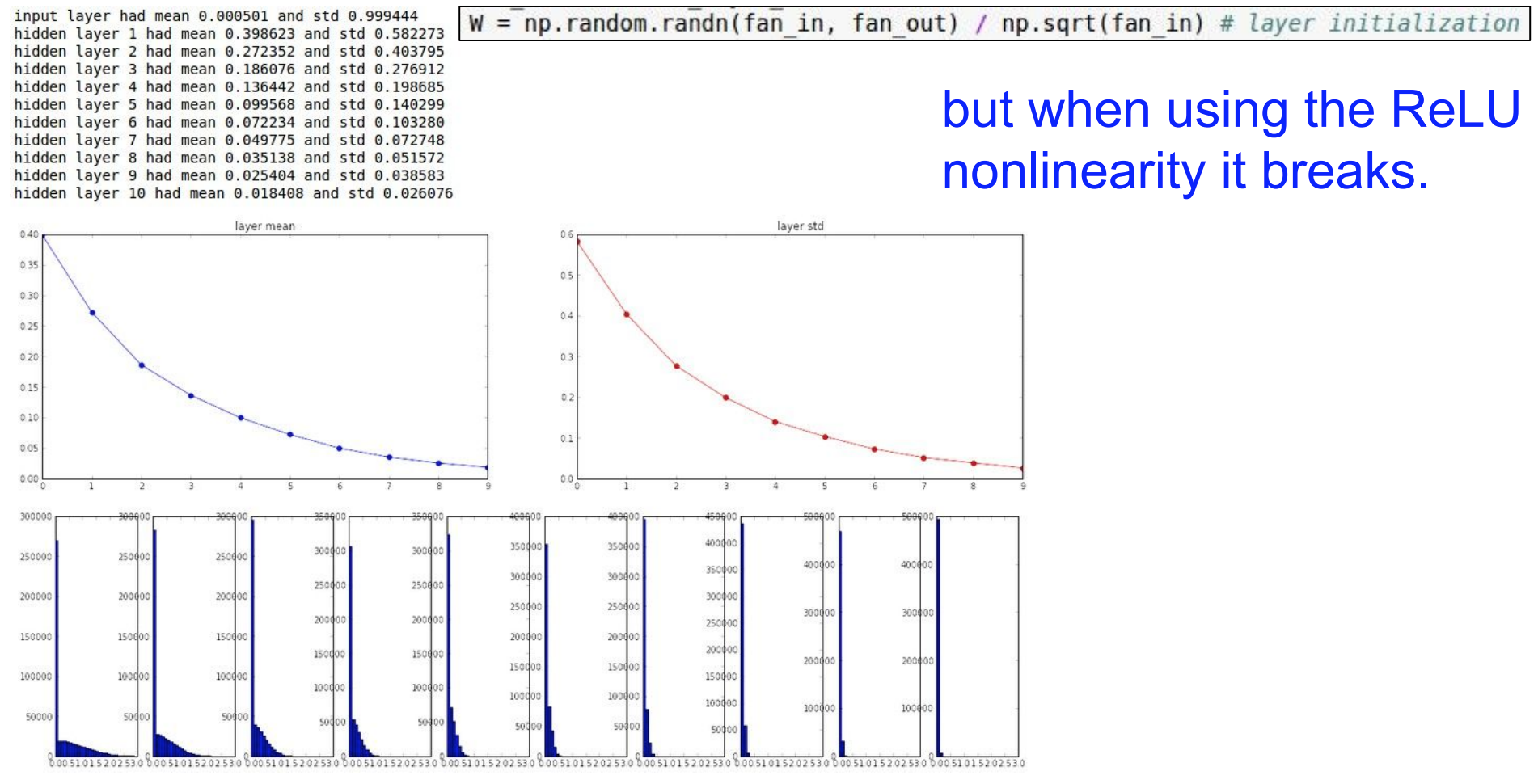
이 방식에 tanh말고 ReLU를 사용하면 다시 문제가 발생한다. 왜냐하면 ReLU를 사용하면 실제로 얻는 분산이 반으로 줄기 때문에 매번 유닛의 약 반을 0으로 설정된다.
- ReLU의 음수 부분은 전부 0으로 되기 떄문이다.
- 따라서 위 그림을 보면 표준편차가 0에 점점 가까워 지는 것을 확인 할 수 있게 된다.

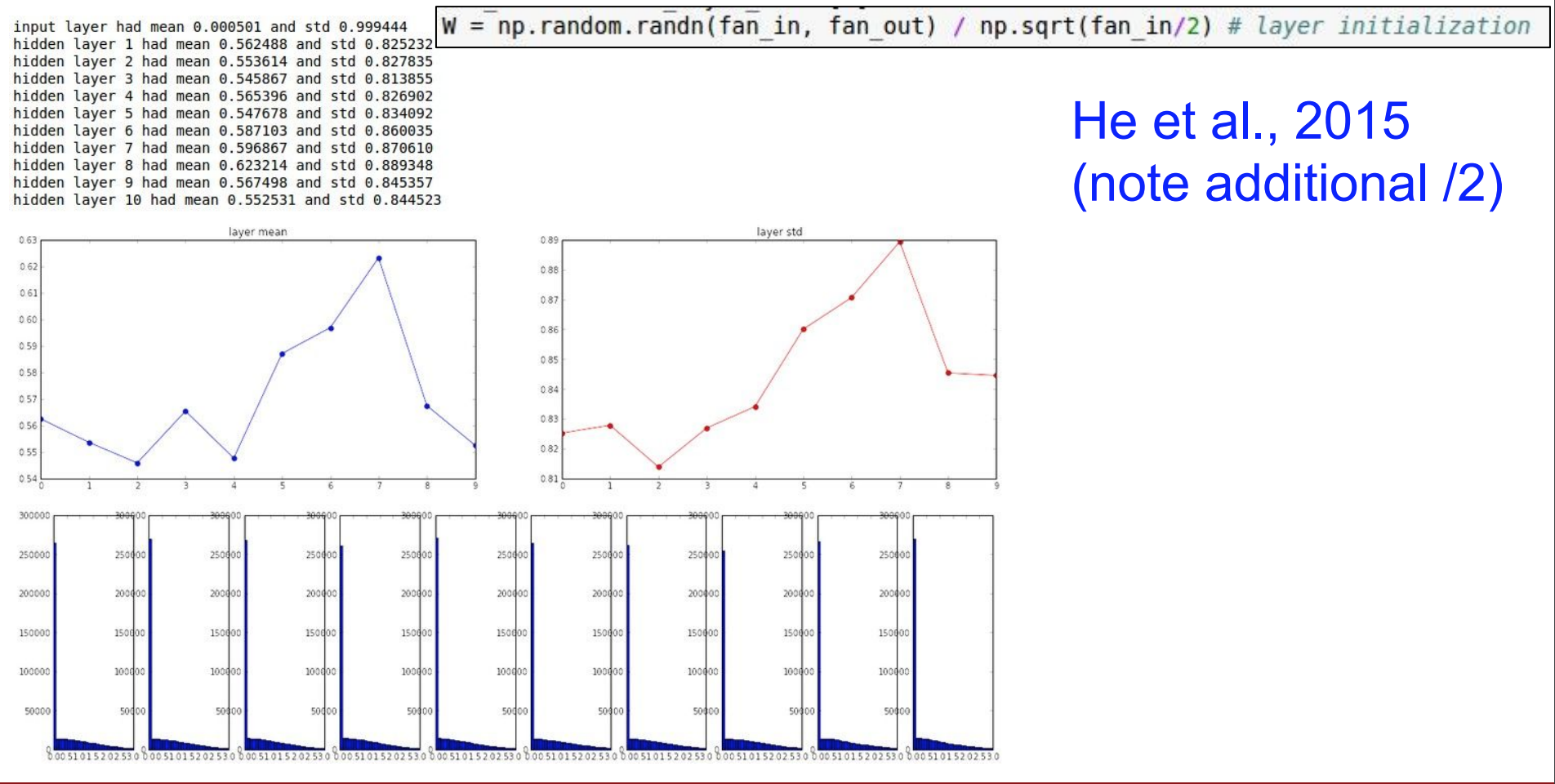
이러한 문제를 해결하기 위하여 2로 더 나눈 추가 항목을 사용하여 이를 설명할 수 있다. (카이밍혜 방법)
- 뉴런이 ReLU로 인하여 절반이 죽어버린다는 근거로 2를 더 나눈 것이다.

마지막 layer의 그래프를 보면 좀 더 나아지는 것을 확인 할 수 있게 된다.
- 따라서 작은 차이에도 weight의 값들에 대해서 주의를 기울이면, 큰 차이가 난다는 것을 강조합니다.

Batch Normalization

Deep Networks를 지나면 W, activation function들에 의해 초기 데이터가 변할 수 있다. 따라서 Depp Networks를 지나도 매 층마다 데이터의 분포를 재조절하여 교정하는 방법이 Batch Normalization이다.

즉, 현재 batch에서의 평균과 분산을 이용해서 훈련 처음부터 batch normalization을 취해주어 모든 층에서 정규 분포를 따르게 하는 것이다.
- Batch란 은닉층에 들어온 dataset을 말한다.
- 이를 사용하면 앞서 배운 W initialization말고 Batch Normalization을 두어 network의 모든 레이어에서 unit 가우스 분포를 가질 수 있는 좋은 위치에 놓도록 할 수 있게 된다.

위 그림과 같이 현재의 batch 에서 N개의 D차원 input data가 있을 때 빨간색 화살표대로 각각의 차원마다(feature element) mean과 variance를 계산할 수 있다.
- 이것이 한 batch 단위에서의 normalize이다.

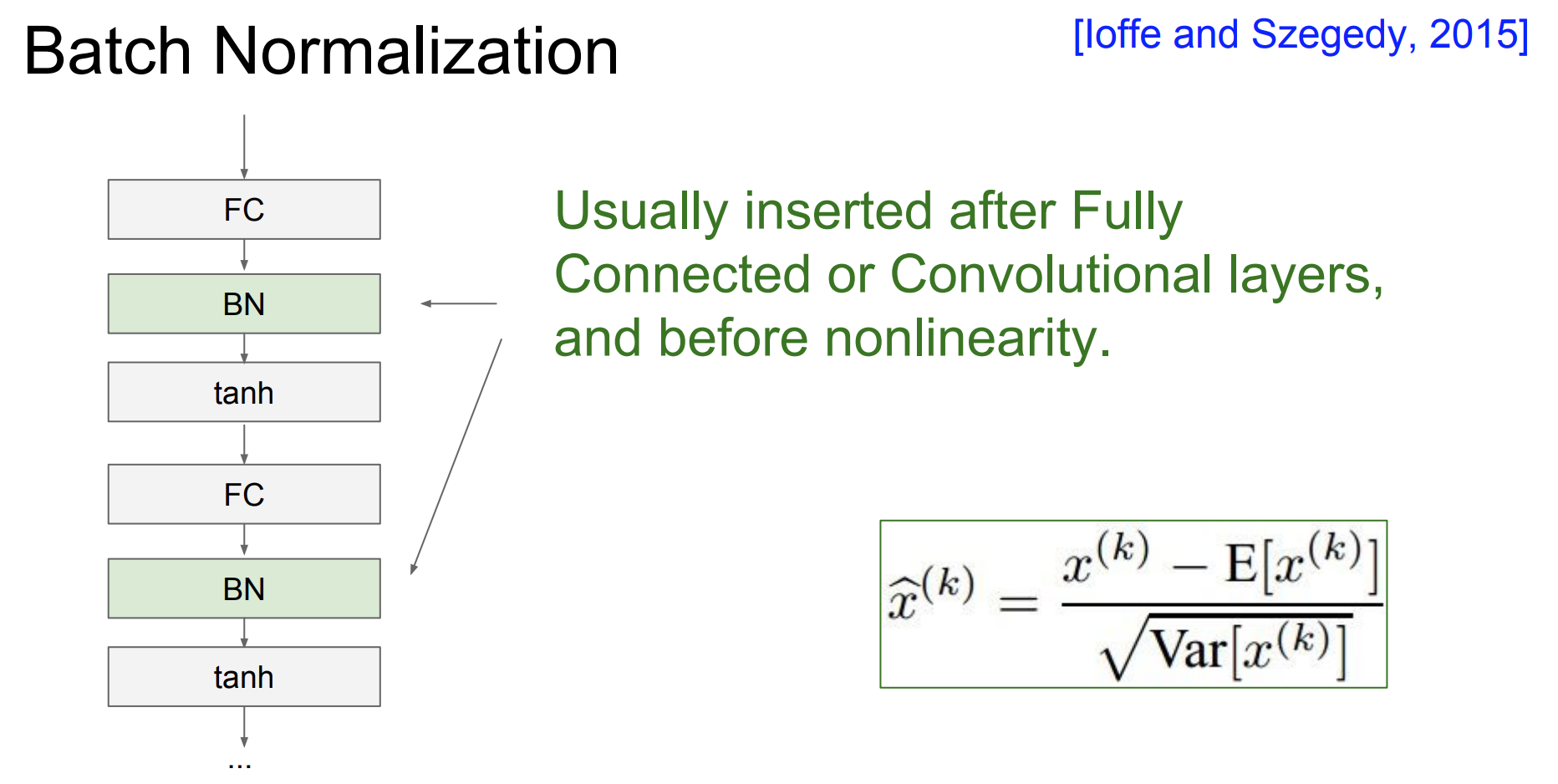
Activation Function을 거치기 전에 convolutional과 fc층 뒤에 BN을 넣어주게 된다.
- Convolutional층에서는 공간적 정보가 손실이 되면 안되기 때문에 activation map당 하나의 평균, 표준편차를 구하여 normalize를 수행하게 된다.
- Batch normalization은 tanh (-1~+1)로 가는 입력값들을 tanh함수의 linear한 부분(기울기가 존재하는 범위)으로 범위를 강제하는 것이다.

이렇게 normalize를 한 값을 다시 변환하고 싶을 때 위 그림의 scale and shift의 식을 이용하면 된다.
- 감마는 표준 편차이기 때문에 scaling의 효과를 주고, 베타는 평균 값이기 때문에 shift의 효과를 주는 것입니다.

Batch normalization이 structure를 흐릴 수 있다는 생각이 들 수 있는데 데이터를 scaling, shfting 해주는 것이기 때문에 데이터의 구조는 바뀌지 않습니다.
- 선형변환이기 때문에 공간 구조가 무너지지 않다고 생각하면 이해하기 쉬울 것이다.
  - 처음부터 그래프의 개형이 변하지 않는다.
Data leakage의 이유 때문에 test dataset 에서 batch norm을 할때에는 train dataset 에서 이용한 mean과 variance를 이용한다.

Babysitting the Learning Process

모델의 전체적인 학습 과정을 어떻게 바라봐야하는지, 등의 전체적인 프레임을 살펴본다.

첫 번째로 preprocessing data이다. 보통 image 데이터는 zero-mean을 사용한다.

두 번째로 choose the architecture이다. 그 다음으로 network를 초기화 하는 것이다.
- 이를 통해 forward pass를 하고 loss가 합리적인지 확인하고 싶다.
- 또한 정규화를 추가를 했을 때 loss가 증가하는지도 확인해야한다.

그리고 학습을 시키는데, sanity check으로 확인하여 매우 작은 데이터가 완벽하게 과적합 하는지 확인을 한다.

이제 전체 데이터를 학습 시키고, Loss를 확인하면서 Learning Rate를 조정한다.

또한 loss는 그대로인데 accuracy가 증가한 이유가 무엇일까?
- 확률이 여전히 꽤 분산되어 있기 때문이다.
- 이 확률들을 올바른 방향으로 약간 이동하게 하면 loss는 그대로지만 정확도가 크게 높아질 것이다.

Hyperparameter optimization

적절한 hyperparameter를 찾는 방법으로 cross-validation를 설명한다. 그것의 방법은 아래와 같다.
- Frist stage: only a few epochs to get rough idea (좋은지 안좋은지 빠르게 알 수 있게 된다.)
- Second stage: 더 오래 길게 수행한다.
- 감지하기 위한 팁이 있다면 loss가 기존과 3배가 증가하면 종료

다음 방법으로는 Grid search, Random search방법이다.
Grid Search는 주어진 범위를 랜덤이 아닌 등간격으로 탐색한다는 점에서 random search와 차이점이 있다.
- 이 경우 특정부분의 특징을 가진 parameter가 무시되기 때문에 random search 방법이 선호된다.

Random search의 방법은 58번의 방법과 같이 랜덤하게 사용하면 된다.

다음은 loss를 해석하는 방법에 대한 설명이 나온다. 위 그림을 보면 lr값은 update의 속도와 방향의 정확도를 전부 가지고 있는 빨간색 그래프가 제일 좋다.

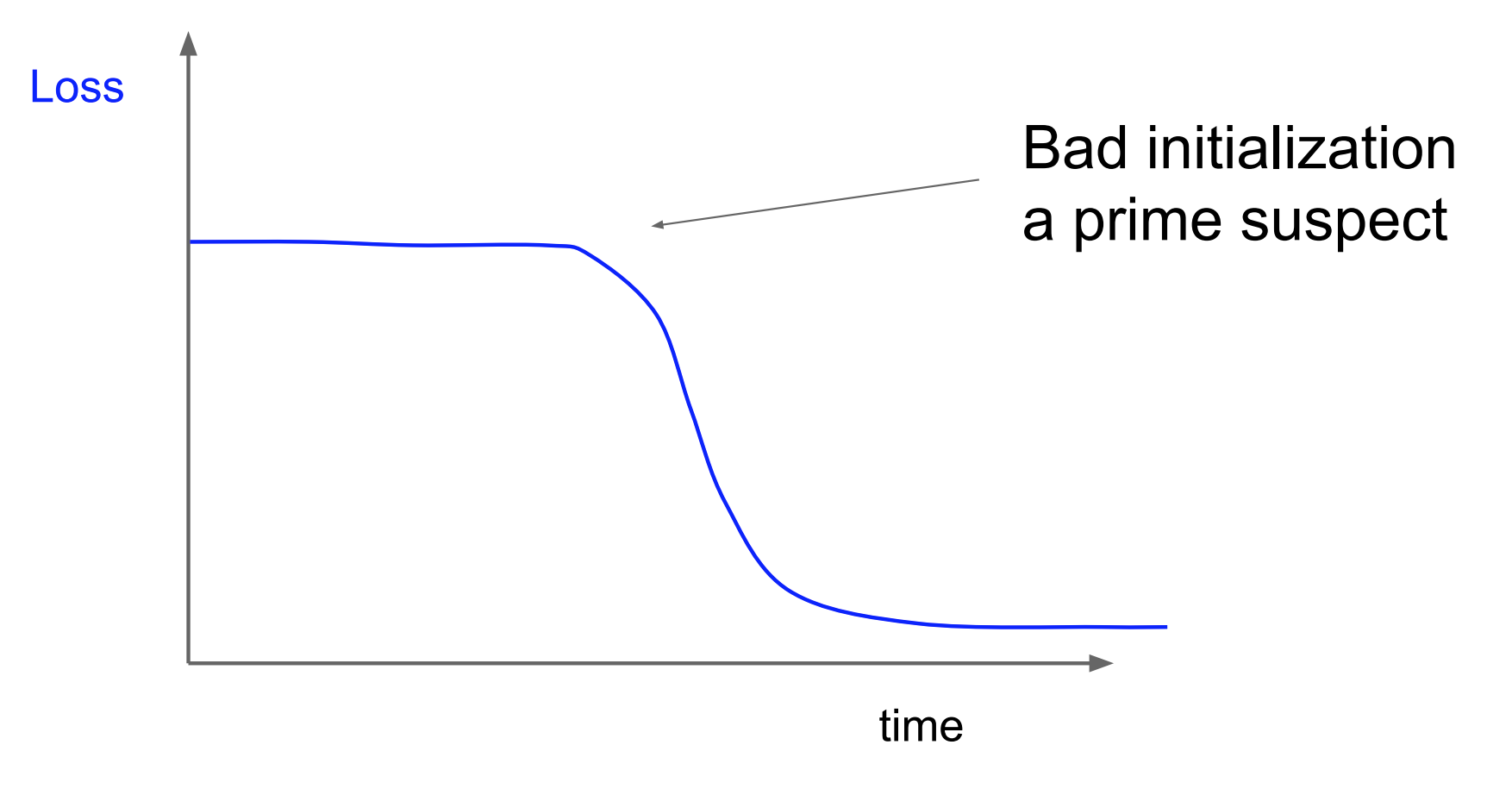
다음 그림은 lr의 값을 너무 작게 선정 했을 때 발생할 수 있는 문제를 나타낸다. lr의 값을 제대로 설정하지 못하여 gradient의 업데이트가 제대로 일어나지 않아서 최적의 방향을 찾는 시간이 너무 오래 걸린 것이다.

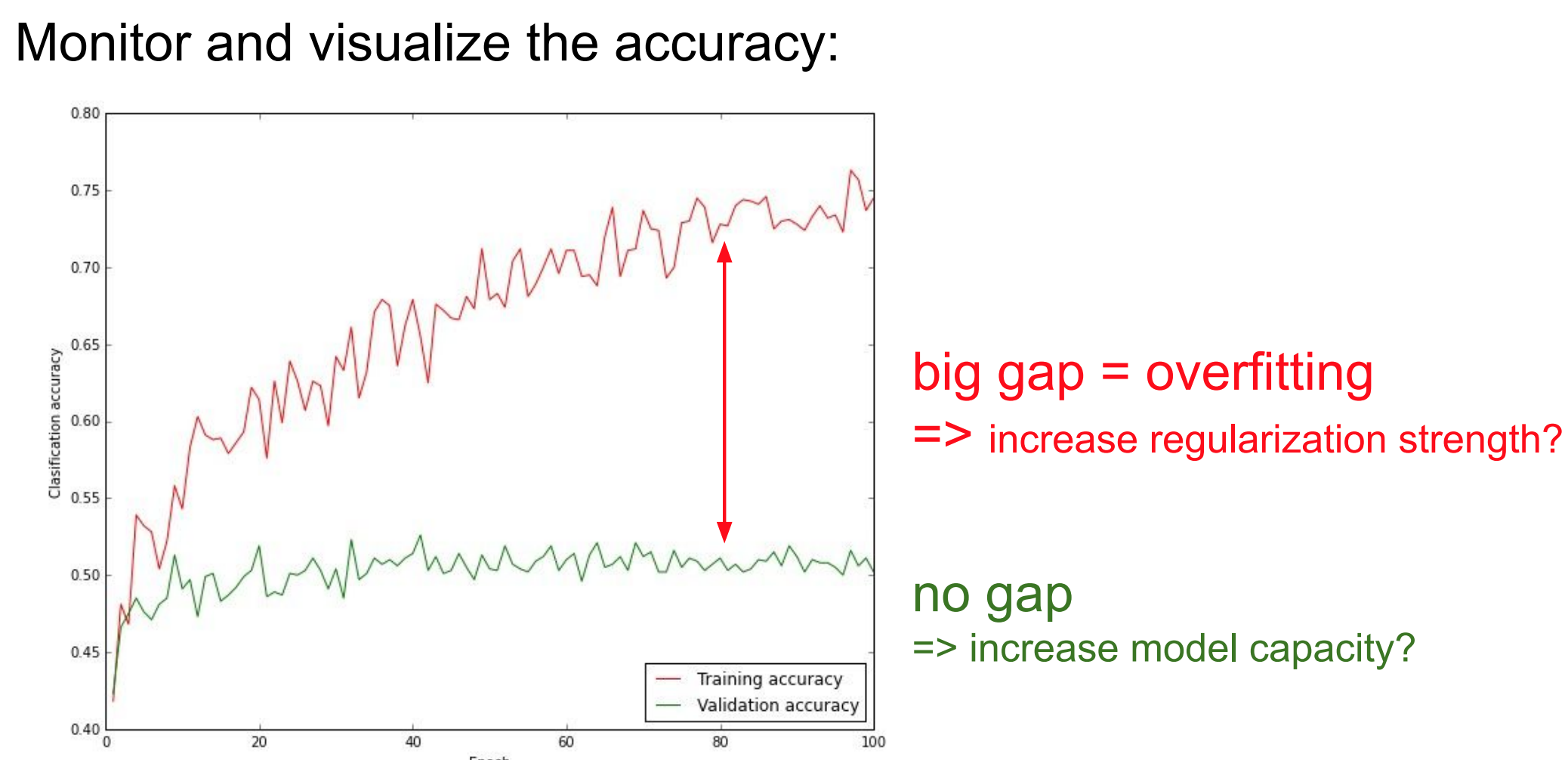
또한 위 그림은 validaiton의 acc값과 training의 acc값의 차이가 크면 안된 다는 사실을 알려준다. 왜냐하면 train에 과적합이 되었다는 사실이기 때문이다.
- 따라서 과적합을 줄여주기 위한 방법으로 규제화, 데이터 셋 더 확보 등을 생각할 수 있을 것 같다.