GoodYoung Dev Blog
Posts Tags Categories
GoodYoung Dev Blog

Contents

[CS231n] 05.Convolutional Neural Networks

GoodYoung included in DL Theory Lecture
   668 words   4 minutes 

개요

  1. CS231n의 5강에 대한 내용을 정리 할 것이다.

  1. 저번 강에서는 W를 업데이트 하는 과정 Chain-Rule과 간단한 Neural Networks에 대해서 배웠는데 이번 강에서는 Convolutional Neural Networks에 대해서 배울 것이다.

A bit of history

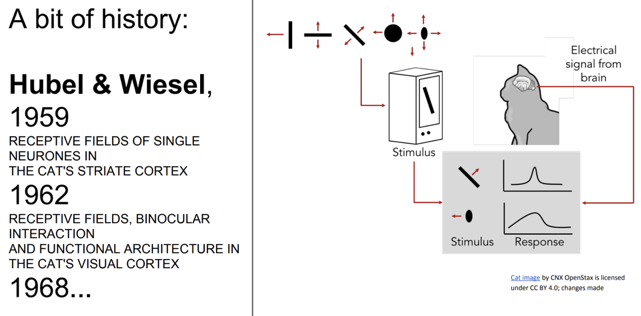
  1. 위 그림을 보면 Hubel & Wiesel이 고양이 실험을 했는데 이때 시각 피질 안의 뉴런이 local receptive field를 가지게 된다는 것을 알게 되었다.

  1. 또한 이렇게 겹쳐지는 receptive field들이 전체 시야를 이루게 된다는 사실을 알게 되었다.

  1. 어떤 뉴런은 low level, 또 어떤 뉴런은 high level의 특징들을 포착하는 것의 조합으로 이루게 된다.

  1. 이러한 지식을 기반으로 image처리를 위해 98년에 Lenet, 2012년에 AlexNet이 등장하게 되었다.

Convolutional Neural Networks

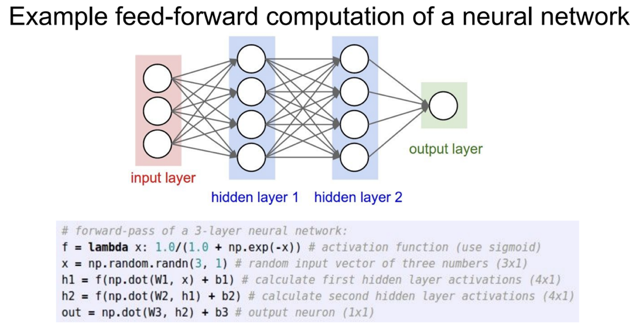
  1. 저번 시간에 node들이 linear하게 모두 연결되어 있는 층을 Fully Connected (FC)층이라고 한다.
  • 또 이 FC층이 행렬의 내적 계산을 통한 아주 효율적인 계산을 할 수 있다고 배웠다.

  1. 따라서 위 그림을 보면 하나의 layer는 하나의 연산을 통해 계산을 하여 편의성을 더해주는 사실을 볼 수 있다.

  1. 하지만 이미지 처리를 할 땐 위의 FC층이 좋지 않다. 왜냐하면 이미지의 spatial(공간적)정보가 손실이 되기 때문이다.

  1. 이러한 문제점을 해결하기 위하여 Convolutional Neural Networks (CNN)이 등장하게 되었다.

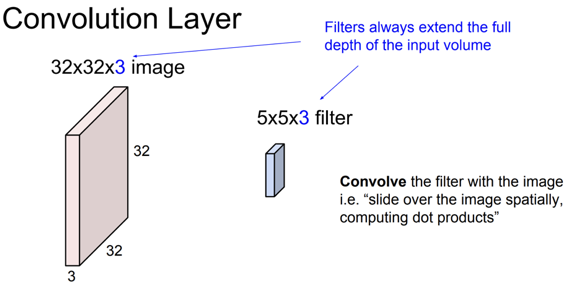
  1. CNN에 대해 더 자세히 알아보면 위 그림과 같은 이미지가 있고 필터가 존재한다. 이 필터는 우리가 linear classification에서 배웠던 W의 역할을 한다.

  1. 이런 필터는 input image위를 아래와 같이 슬라이딩 하면서 요소별 곱을 하고 그것을 또 하나의 합으로 나타낸다.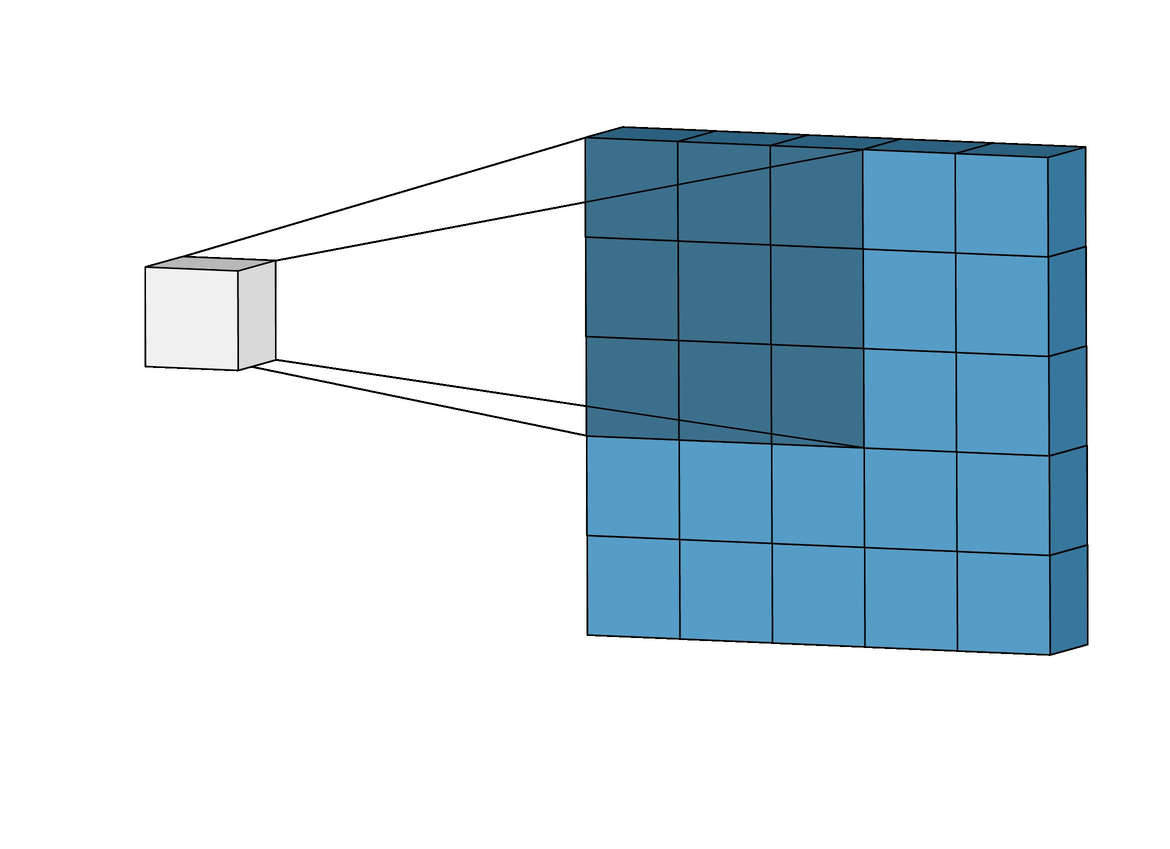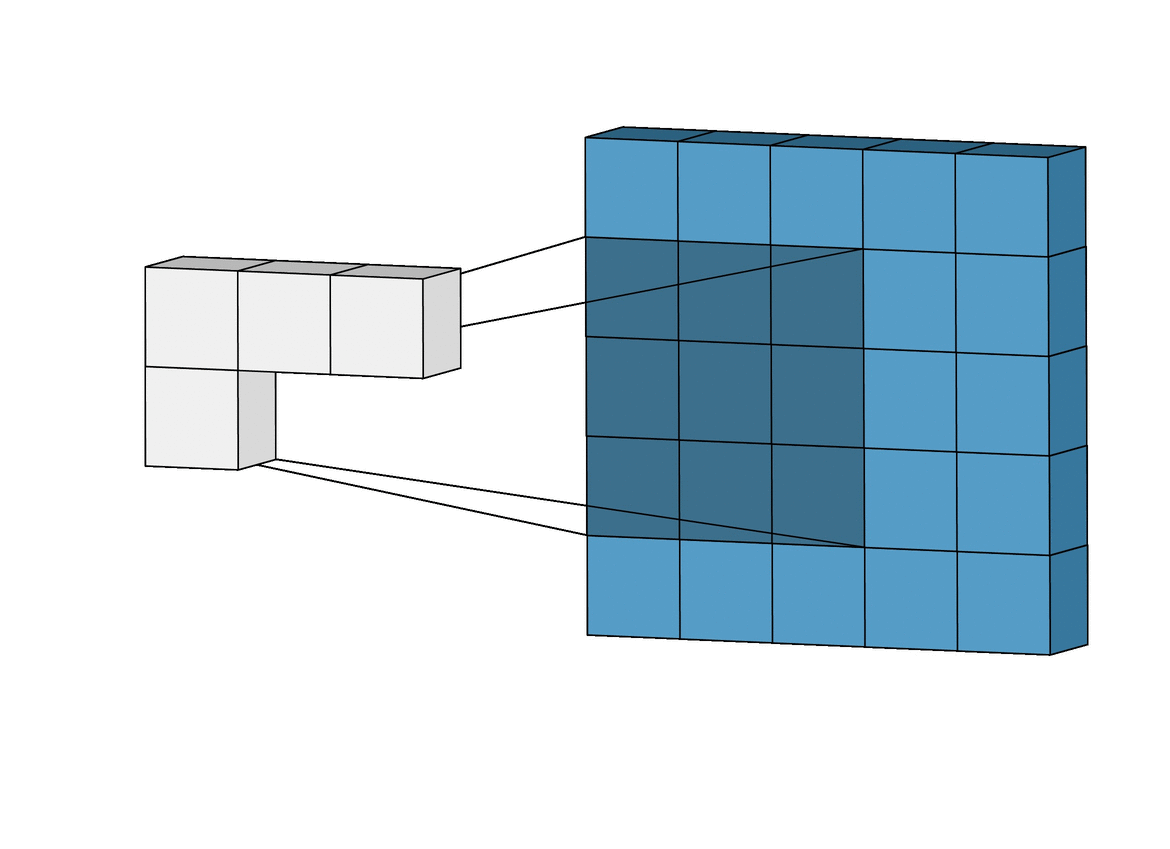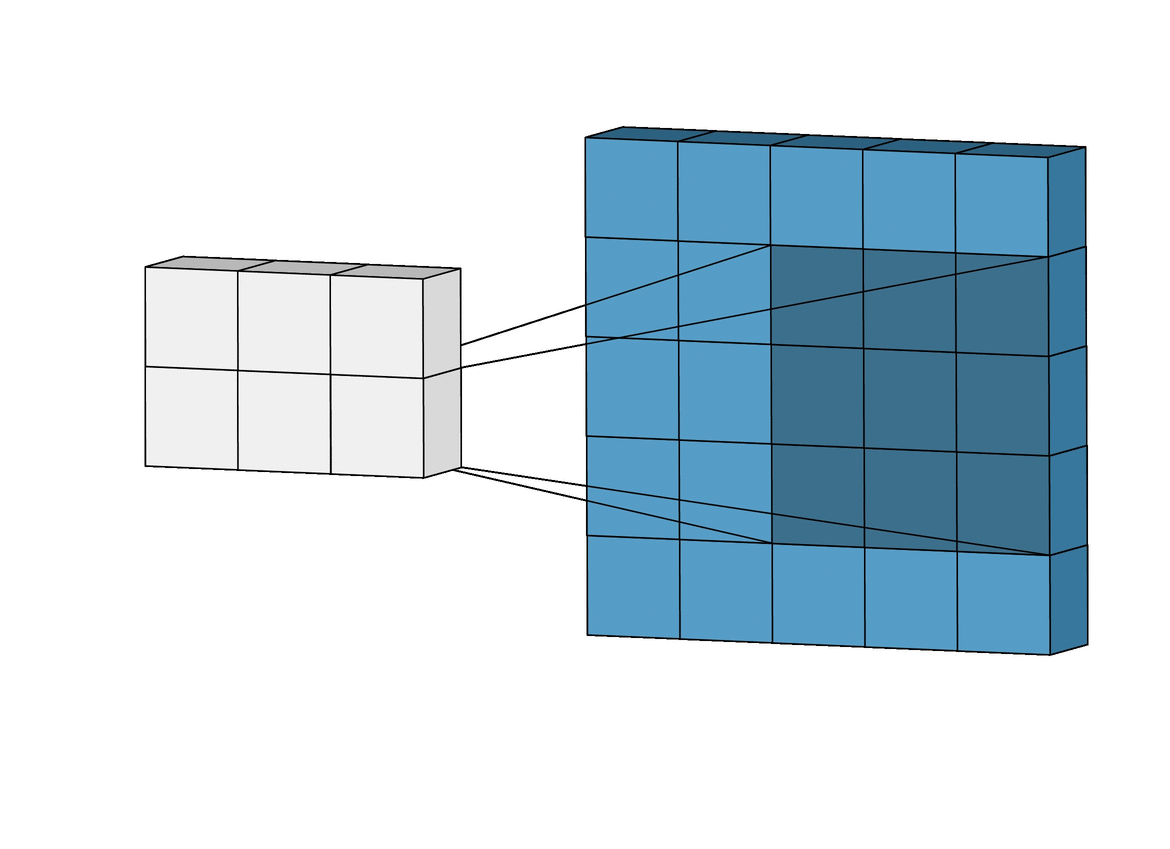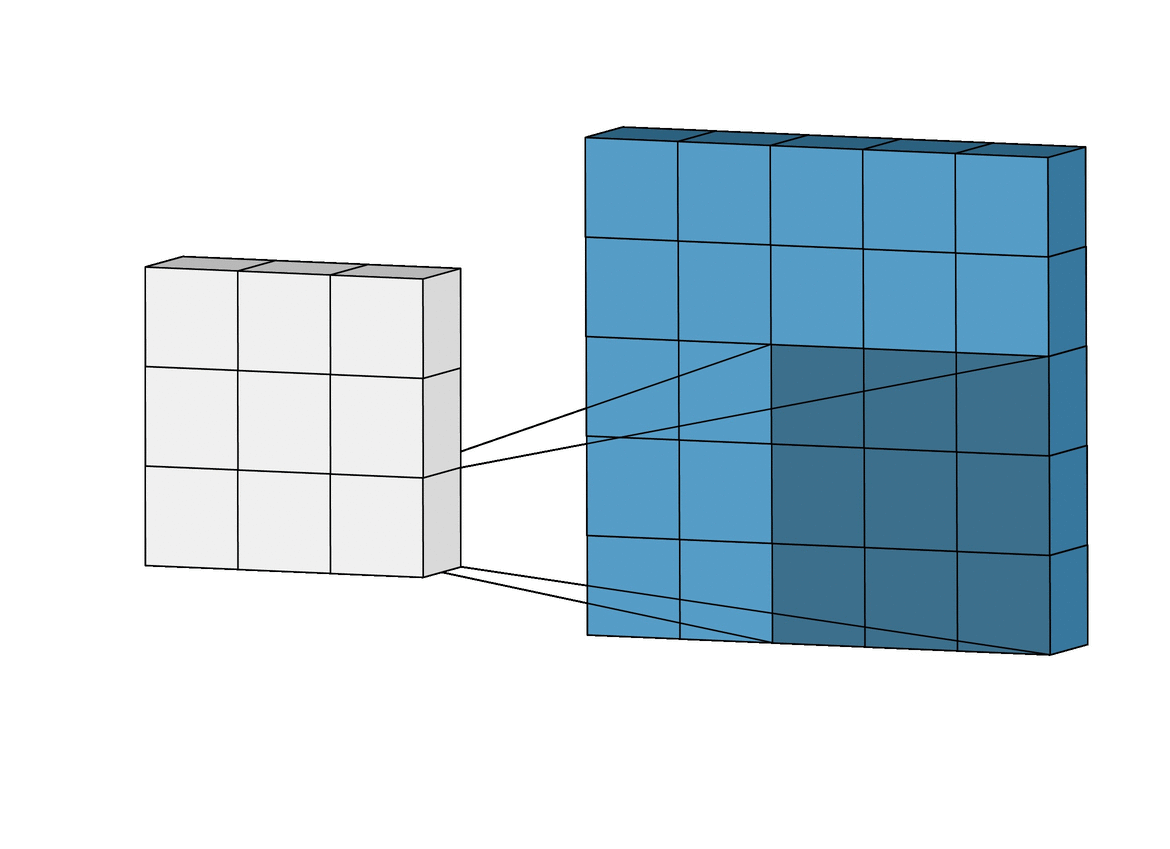

    • 위 그림에선 3 * 3의 크기의 filter가 5 * 5의 크기의 image 위를 슬라이딩 하고 있다.

  1. 이 filter에 중요한 사실이 있다. 바로 filter의 depth 크기는 input volume의 depth랑 항상 같다는 점이다.

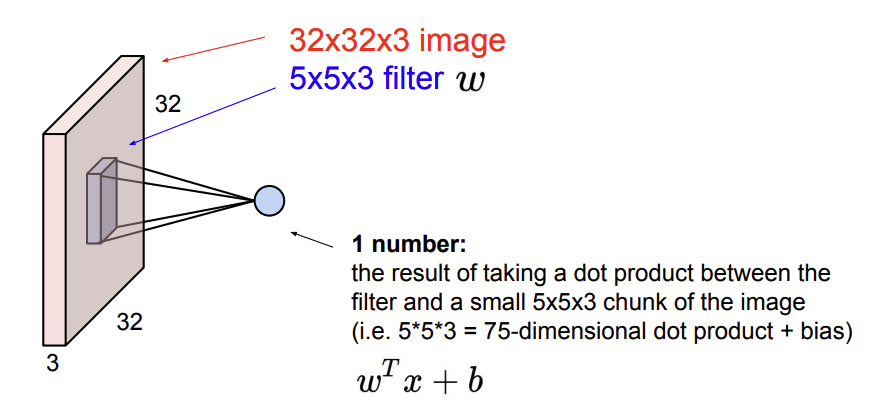
  1. 왜냐하면 우리가 시각적으로 보기에 image위를 슬라이딩 하는 것 처럼 보이지만 실제로의 연산은 $w^Tx$에서 image에서 filter가 겹쳐지는 부분만큼 가져온 후 1차원으로 늘린 연산이다.

  1. 따라서 위 그림과 같이 5*5*3의 크기인 filter연산은 곧 75-1D의 내적 연산(1차원)을 수행하는 것으로 이해하면 될 것 같다.

  1. 이렇게 연산을 수행하기 때문에 input volume의 depth랑 filter depth랑 같아야 filter의 내적 연산을 수행할 수 있게 된다.

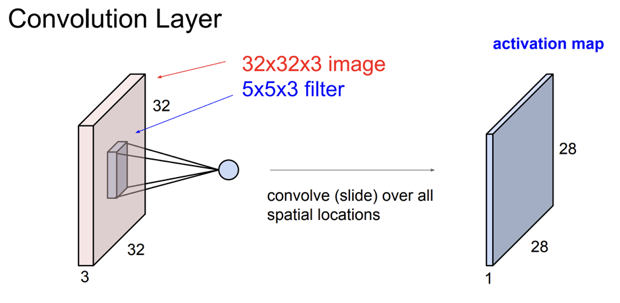
  1. 이렇게 filter가 슬라이딩을 하여 연산을 한 번 모두 하면 위 그림과 같이 하나의 activation map이 나온다.

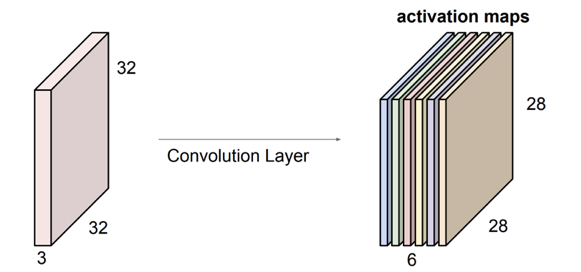
  1. 만약 필터가 6개가 있다면 앞서 말한 내적 연산을 6번 수행하여 ouput의 depth가 6인 activation map이 나오게 된다.
  • 각 필터는 input volume에서 특정 유형의 템플릿이나 개념을 찾는다.
  • 6개의 각각 다른 가중치를 지닌 activation map으로 생각하면 된다.

  1. 이런 layer들을 연속적으로 쌓아나가면 그것이 convolution network가 된다.

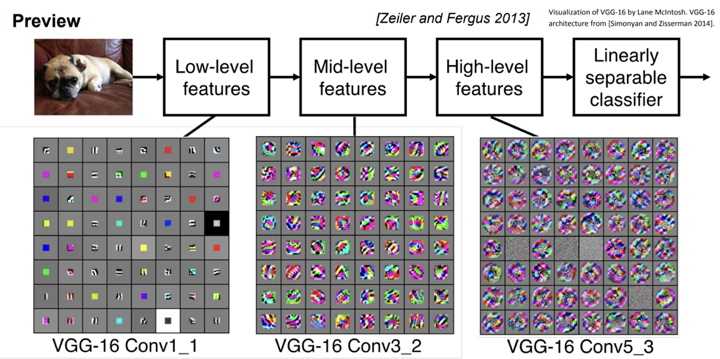
  1. 이런 convolution network에서는 처음에 low-level(edge 등등)의 특징을 추출하고 점점 깊어지면 high-level의 복잡하고 추상적인 개념들이 나타나게 된다.

  1. 이 정보들을 FC층에 넣고 각 class 수의 확률 연산을 하게되면 분류가 이루어진다.
  • 왜 FC층이 필요하며, 어떻게 분류가 이루어지는지 의문을 가졌다.
  • high-level features는 넓은 reception field를 가지고 있다. (점점 깊어질 수록 이미지의 resolution이 줄어들기 때문)
  • 이러한 복잡하고 풍부한 정보를 포함하고 있는 feature들을 linear하게 놓고 모든 정보를 연결(Fully connected)을 하여 각각의 class별 weight를 계산을 하게 되면 해당 이미지가 class별 확률(softmax)이 나오게 될 것이다.
  • 따라서 CNN으로 feature를 추출하고 FC 층에서 분류하는 이유는 이러한 과정을 통해 각 클래스별 확률을 효과적으로 계산할 수 있기 때문입니다.

  1. 이러한 방법들은 앞서 history에서 말한 인간의 인식 능력에서의 시각피질과 유사한 특징을 보이는 것을 알 수 있다.

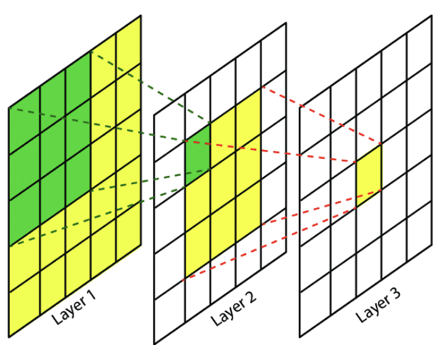
  1. 픽셀은 항상 일관된 순서를 가지며, 서로 인접한 픽셀끼리 영향을 준다.

  1. 만약 모든 근처의 픽셀이 빨간색이라면 해당 픽셀도 빨간색일 가능성이 높다. 이렇게 픽셀은 주변 픽셀 값과 비교하여 정보를 추측할 수 있습니다. 이런 특성을 locality라고 합니다.

  1. 따라서 위 그림과 같이 sub sampling과정을 통해 image의 resolution을 줄이고 local feature들에 대한 연산을 통해 global feature(high-level)로 나아가 weight 변수를 줄이고 변화에 무관한 invariance를 얻게 되는 것이다.

  1. Convolution의 표준 정의는 다음과 같다. $$f[x, y] * g[x, y] = \sum_{n_1 = -\infty}^{\infty} \sum_{n_2 = -\infty}^{\infty} f[n_1, n_2] \cdot g[x - n_1, y - n_2]$$

  1. 이제까지 대략적인 Convolution이 작동하는 방법에 대해 알아보았고 다음은 filter의 Stride에 관한 내용이다.

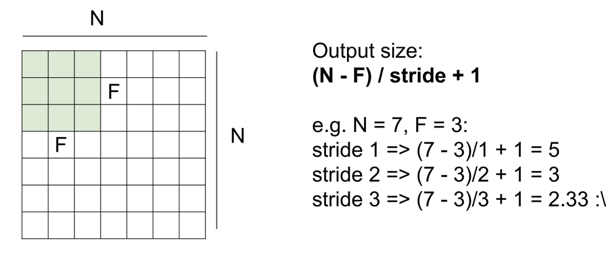
  1. Stride는 filter의 보폭, filter가 슬라이딩을 할 때 얼만큼 움직일지를 결정하는 것이다.

  1. filter가 한 번의 연산을 거친 후 output size는 다음과 같은 식으로 구한다.

  1. 하지만 이것만 활용하면 filter가 가장자리의 정보를 많이 얻기 쉽지 않다. 그래서 나온 개념이 padding이다.

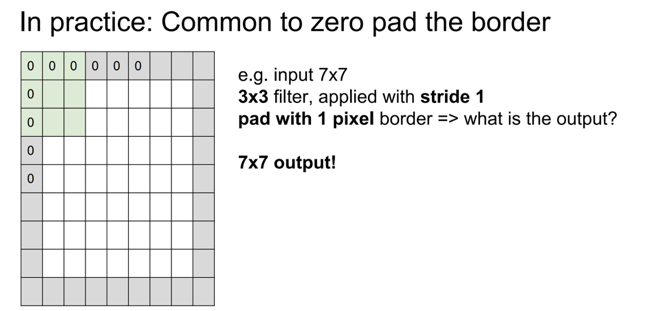
  1. Padding은 input에 0을 더하여 가장자리의 정보도 얻을 수 있게 한다.

  1. 또한 Padding은 network가 깊어질 때 image의 resolution를 동일하게 유지시키려고도 많이 사용하게 된다.

  1. 따라서 Padding까지 고려한 output size는 다음과 같다. $$ (\frac{W+2P-F}{S}, \frac{H+2P-F}{S})$$

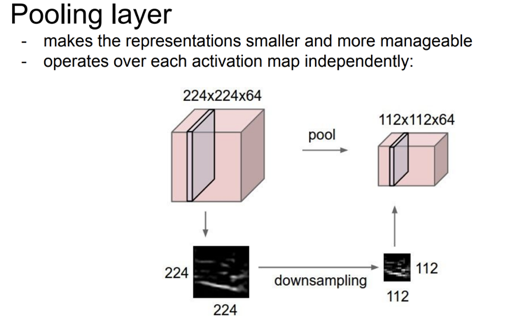
  1. 다음은 pooling에 관한 설명이다. Pooling은 이미지의 resolution을 줄이는 역할을 하게된다. 여기서 중요한 점은 오로지 resolution($(W,H)$)의 변화만 있지 depth에 변화는 없다.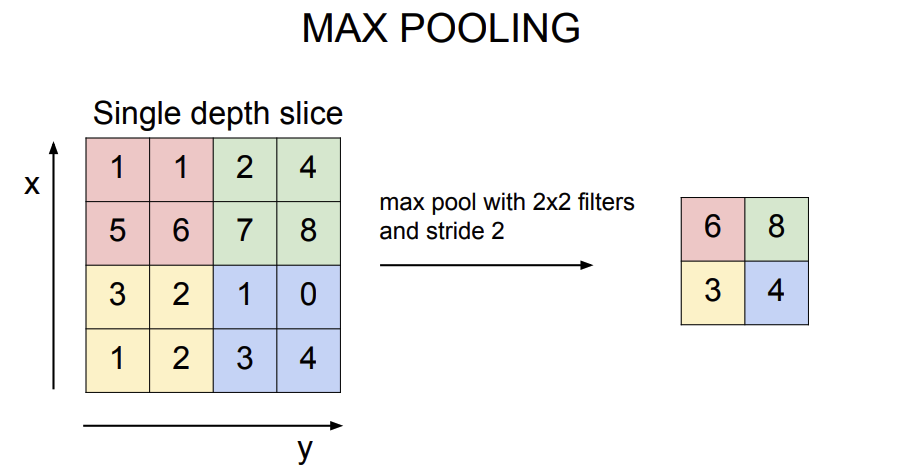

    • pooling에 방법에는 크게 두가지가 있는데 average pooling과 max pooling이 있다.
    • max pooling의 연산은 위 그림과 같고 주로 max pooling을 사용한다.

Reference

Updated on 2024-07-12
 Chain Rule, Neural Networks, CS231n
Back | Home