[CS231n] 04.Introduction to Neural Networks

개요

0. CS231n의 4강에 대한 내용을 정리 할 것이다.

1. 저번 강에서는 Loss Function과 Optimization에 대해서 배웠는데 이번 강에서는 W를 업데이트 하는 과정인 Chain-Rule과 간단한 Neural Networks에 대해서 배울 것이다.

Backpropagation

2. 지난 과정에 gradient에는 두가지 종류가 있다고 배웠다. 그 중 빠르고 정확한 analytic gradient에 대해서 활용해볼 것이다.

3. 각 과정의 연산 과정을 Computational graph을 활용하여 표현한다면 analytic gradient를 활용할 수 있게 된다.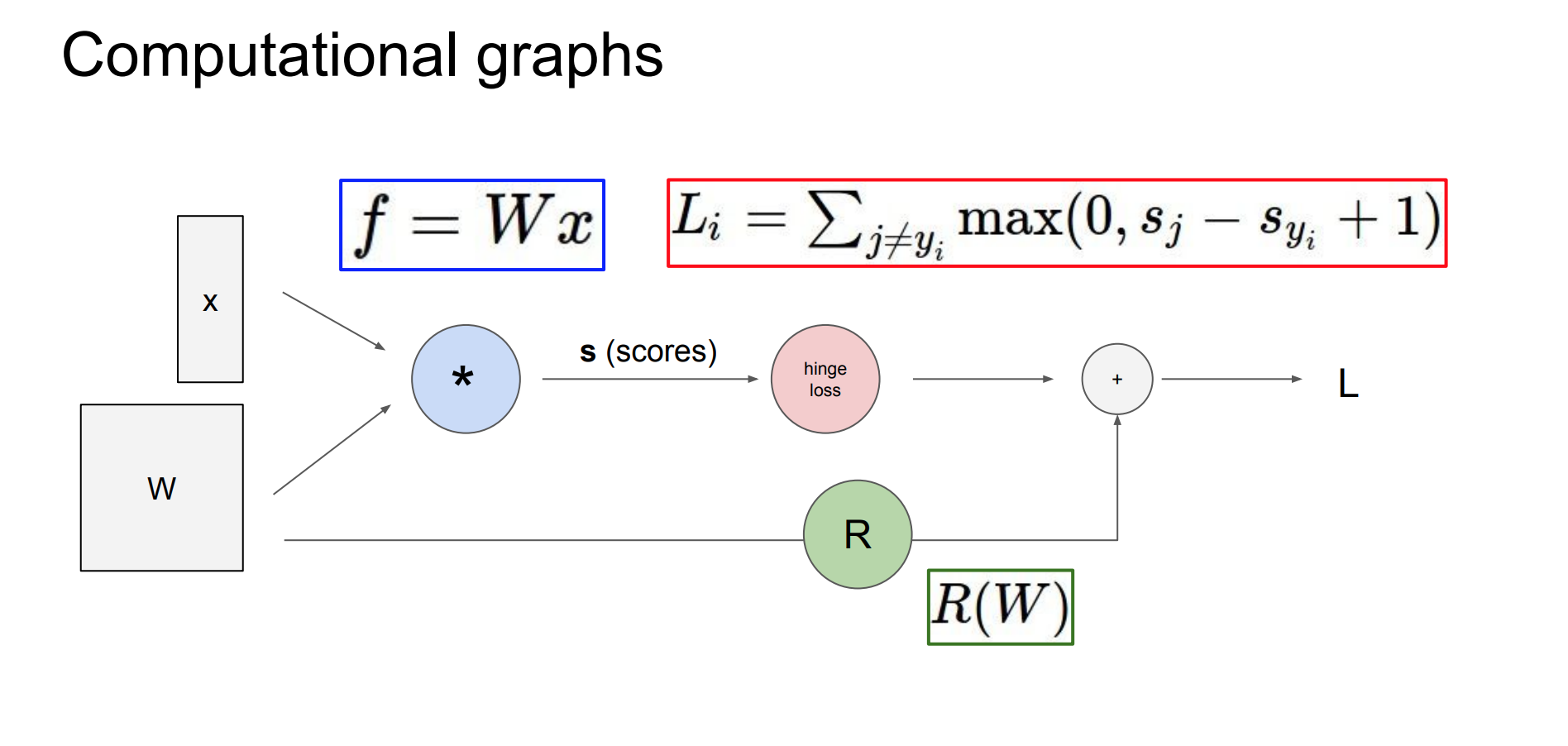

   

4. 이를 통해 함수는 BackPropagation이라는 기술을 사용하고, gradient를 얻기 위하여 Chain-rule를 활용한다.

5. BackPropagation의 과정은 다음과 같다.

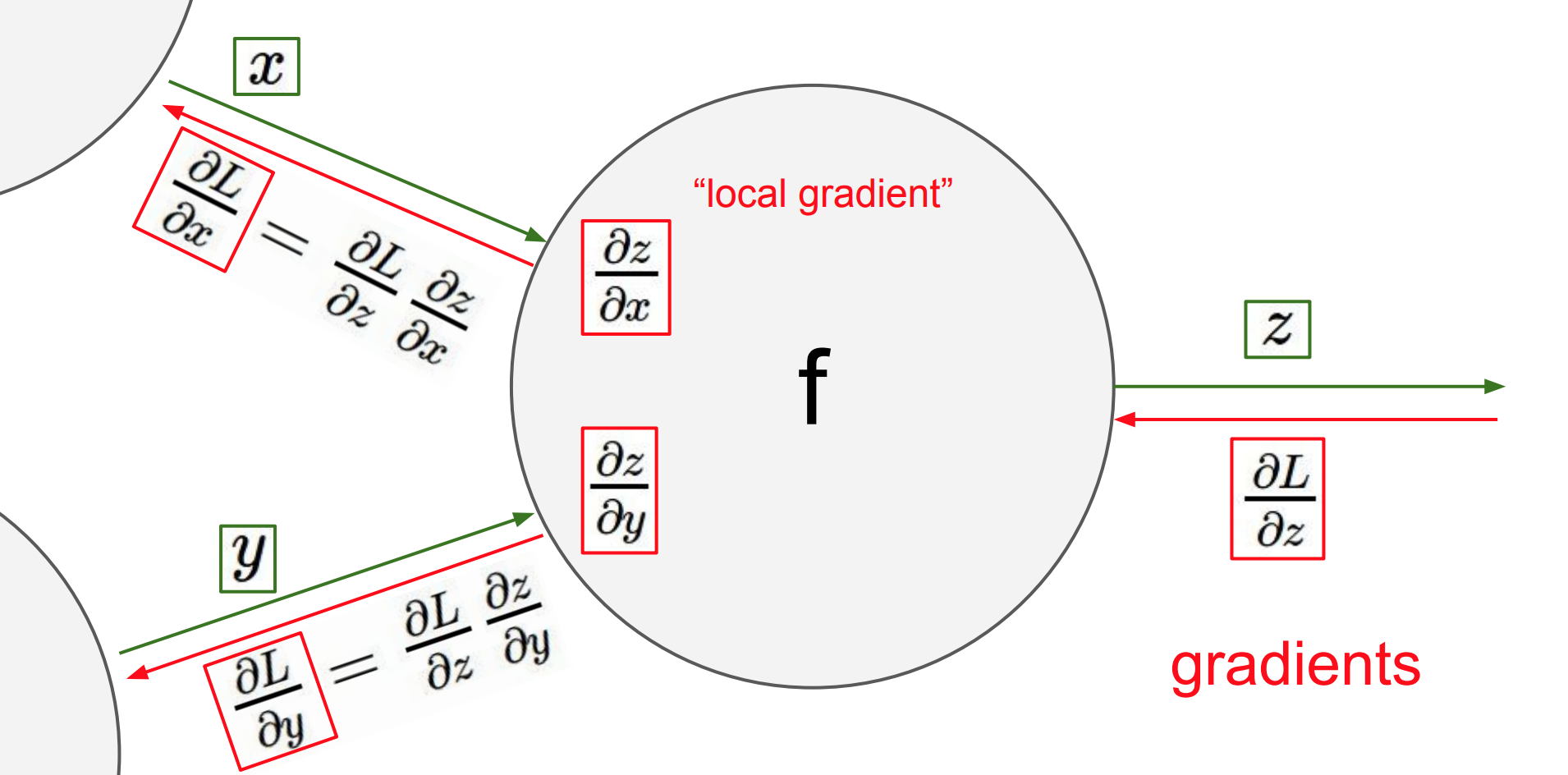
6. 각 입력이 local node로 들어오고 다음 노드로 직접 전달된다.

7. local gradient는 이때의 입력된 노드의 출력의 gradient이다.
   • 각각의 입력마다 그때의 local gradient를 구한다.
   • 즉, z에 대한 x로의 미분, z에 대한 y로의 미분을 구한다.

8. 이를 Forward Pass (Foward Propagation)이라고 한다.

9. Forward Pass의 맨 마지막에는 loss function을 통한 loss가 나온다.

10. Forward Pass가 모든 노드가 진행이 되었으면 Backward Pass (Back Propagation)이 진행된다.

11. 이때 Back Propagation은 수많은 계산을 거쳐 나온 loss에 대한 z의 미분을 나타내고 이는 global gradient (위 그림에선 빨간색 글씨로 gradients라고 표기)라고 칭한다.

12. 이때 그럼 loss에 대한 x, y의 미분값을 구할 수 있게 되는데 이때 활용되는 개념이 Chain-rule이다.

13. Forward Pass로 구한 local gradient의 값과 그 노드의 global gradient를 곱하면 우리고 최종적으로 원하는 gradient가 나오게 된다.

• $gradient = local \ gradient * global \ gradient$

14. 이런 Computational graph에서 그룹화를 할 수 있다는 사실도 알 수 있다.
    

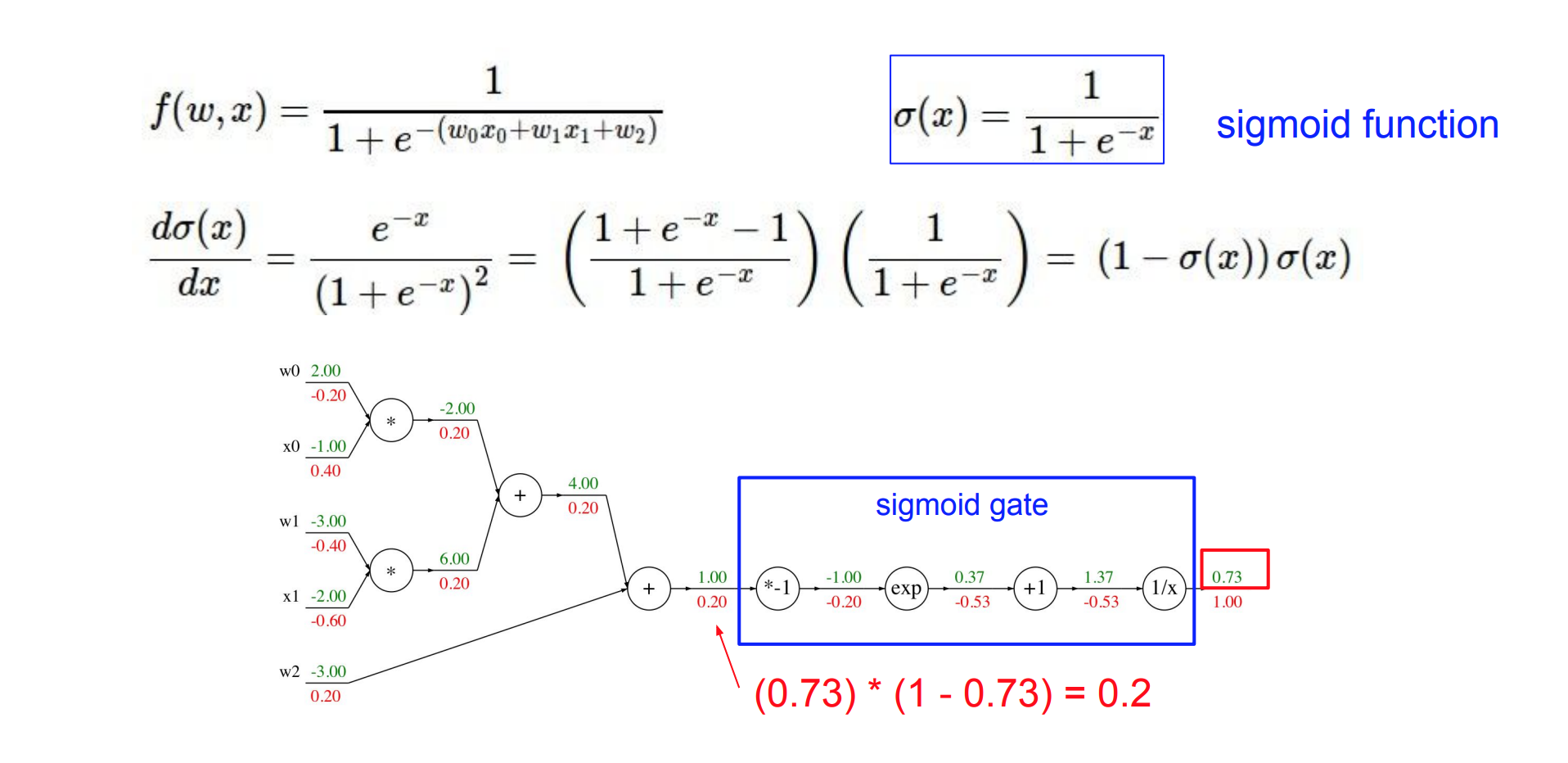
    • 위 그림을 보면 sigmoid gate로 하나의 노드로 묶어서 계산 할 수도 있다.
    • 따라서 얼마나 그룹화를 하여 노드를 표현할 것인지에 대한 고민이 필요할 수 있다.

15. 또한 Back Propagation에는 3가지 패턴이 존재한다고 한다.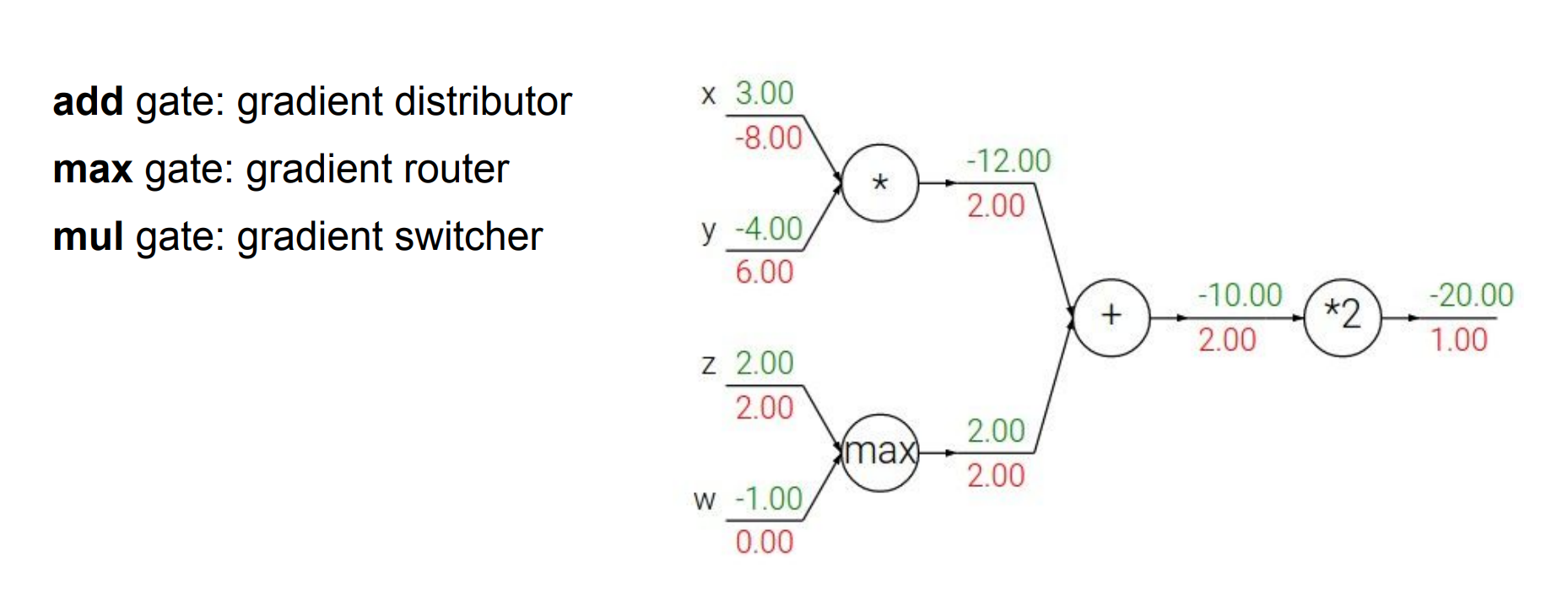

    • add gate
      • gradient 전달하는 역할
    • max gate
      • 한 방향으로 gradient 모두 전달하는 역할
    • mul gate
      • 서로 gradient 전환하는 역할

16. 종합적으로 위에서 배운 Back Propagation을 아래와 같이 일반화된 식으로 표현한다.

$$ \frac{\partial f}{\partial x} = \sum \frac{\partial f}{\partial q_i} \cdot \frac{\partial q_i}{\partial x} $$

17. 이제 위에서 배운 Back Propagation에서 변수가 벡터라고 생각한다면 gradient는 Jacobian matrix로 표현할 수 있게 된다.

• Jacobian matrix: 각 요소의 미분을 포함하는 행렬

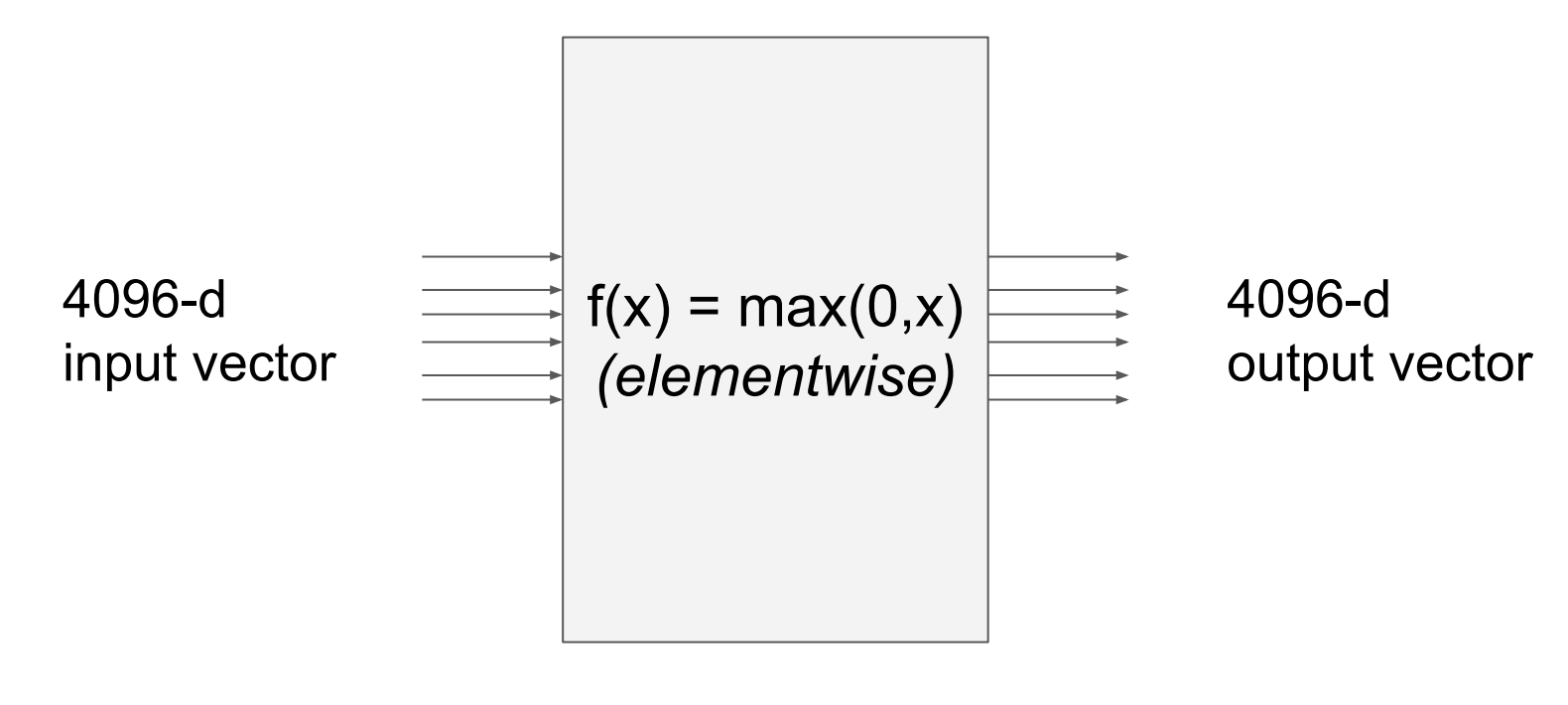
18. 따라서 4096의 input이 들어온다면 이 Jacobian matrix의 크기는 $4096 * 4096$ 일 것이다.

• 이때 gradient의 각 요소는 함수의 최종 출력에 얼마나 영향을 미치는가를 정량화 한 값으로 표현이 되고 이는 결국 편미분한 값과 이어지게 된다.
• 따라서 입력의 어떤 차원이 출력의 어떤 차원에 영향을 주는지, 그래서 Jacobian matrix는 입력의 각 요소가 오직 출력의 해당 요소에만 영향을 주기 때문에 대각 행렬이 될 것이다.

Neural Networks

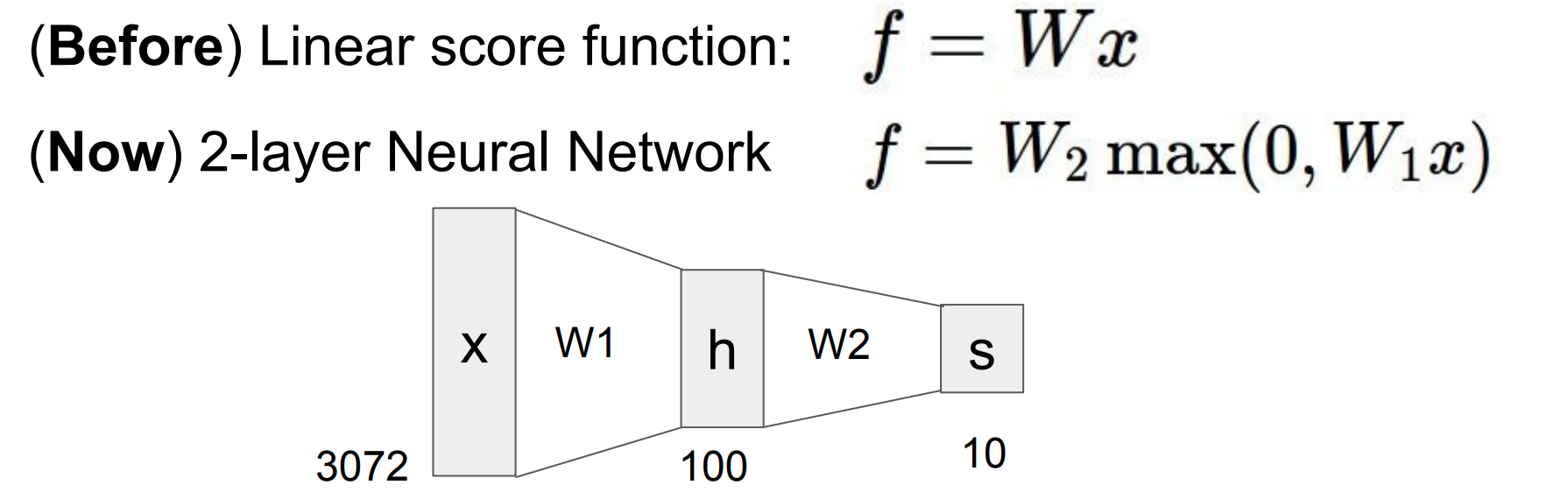
19. 위 그림 처럼 2계층 신경망을 얻기 위해 다른 것 위에 비선형 변환을 하면 된다. 이렇게 계속 층층 쌓아가면 Deep Neural Network의 형태가 된다.

• 위의 W1, W2는 각각 gradient로 학습 시키고, 그 gradient들은 Chain-rule으로 계산하여 구한다.

20. 이런 비선형성의 특징을 표현하기 위해 activation function이라는 함수가 존재한다. 이는 강의 후반부에 더 자세히 다룬다고 한다.

21. 아래는 이 Forward pass과정을 코드로 표현한 것이다.

      f = lambda x: 1.0/(1.0+ np.exp(-x)) # sigmoid (activation function)
      x = np.random.randn(3, 1) # random input vector
      h1 = f(np.dot(W1, x) + b1) # calculate first hidden layer
      h2 = f(np.dot(W2, h1) + b2) # calculate second hidden layer
      out = np.dot(W3,h2) + b3 # output neuron (1*1)
    

Reference

• https://chasuyeon.tistory.com/entry/cs231n-4%EA%B0%95-%EC%A0%95%EB%A6%AC-Introduction-to-Neural-Networks