[CS231n] 03.Loss Functions and Optimization

개요

0. CS231n의 3강에 대한 내용을 정리 할 것이다.

1. 저번 강에서는 선형 분류기에 대해서 공부를 했는데 이때 어떻게 이미지의 가중치인 W의 값들의 badness를 판단하는지(loss function), 또 W의 값들을 업데이트 하는 방법(optimization)에 대해서 집중적으로 다룰 것이다.

Loss Function

2. Loss Function이란 W를 가져와서 점수를 보고 얼마나 정량적으로 좋은지 나쁜지 알려주는 함수이다.

• 또는 실제값과 예측값의 차이를 수치화 해주는 함수이다.

3. Loos Function의 기본 식은 아래와 같다.

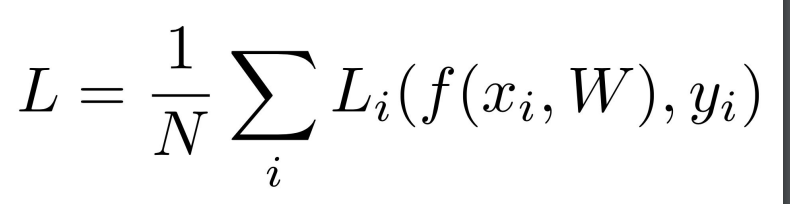
• xi: pixel value
• yi: predict label - f: predict y
• Li: loss function - L: loss mean

4. 따라서 위 식을 통해 어떤 W가 가장 좋은 결과를 가져오는지 정량적으로 판단할 수 있게 된다.

Multiclass SVM Loss

5. 다음으론 image classification에 적합한 multi-class SVM Loss에 대한 설명이다.

6. loss function의 식은 아래와 같다.

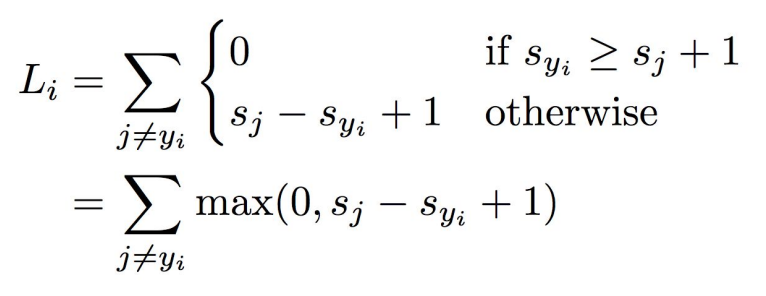
• sj: 잘못된 label의 score
• syi: 제대로 된 label의 score - 1: safety margin

7. 따라서 위 식은 제대로 예측을 했고 그 값이 safety margin보다 뛰어나다면 loss는 0을 나타내고, 그것이 아니라면 잘못된 label과 정상 label간의 차이만큼이 loss인 것을 알 수 있다.

8. 이를 그래프로 시각화를 하면 아래 그림과 같은데 이를 hinge loss라고 한다.

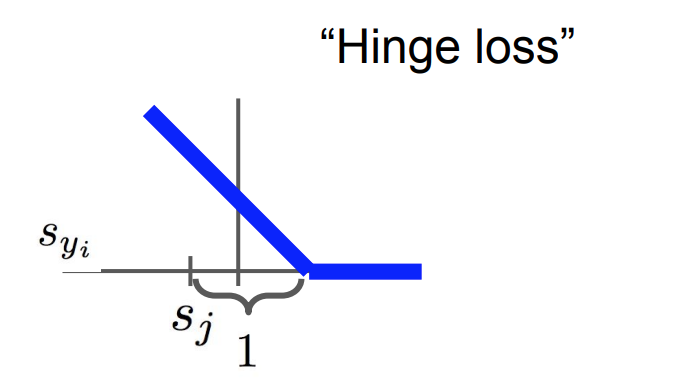
9. 이 그래프를 통해 알 수 있는 사실은 잘 분류된 point는 loss가 작거나 없고, 잘못 분류된 point는 loss가 높다.

• 잘 분류되었을 수록 syi가 클 것이다.
• 그러므로 sj - syi의 식에서 음수값이 나올 가능성이 크다.

10. 다음은 hinge loss에 관하여 6가지의 질문이 나온다.

• Q1: 잘 예측 했을 경우 데이터가 미세하게 변한다고 해서 loss의 값이 변하지는 않는다.
• Q2: hinge loss의 최솟값은 0, 최대값은 무한대일 것이다. (class score가 엄청 낮은 음수 값을 가지고 있다면)
• Q3: W를 임의의 작은 수로 초기화를 할 때 sj - syi의 값이 0일 경우 classes_num - 1의 값이 나오게 된다.
  • 이는 debugging시 유용하다.
  • 훈련 시 초기의 loss값이 classes_num - 1이 아니라면 과정 중 어떤 것이 잘못되었는지 다시 볼 필요가 있다.
• Q4: 정답 class도 계산을 한다면 기존 loss에 1이 증가한 형태일 것이다.
• Q5: Summation이 아니라 Mean이라도 loss의 값은 변함 없다. (rescale만 된다. 큰 영향 없다.)
• Q6: 아래의 그림과 같이 제곱항으로 변경한다면 결과는 달라진다. 선형적이었던 관계를 비선형적으로 바꿔서 표현이 된다.
  • 
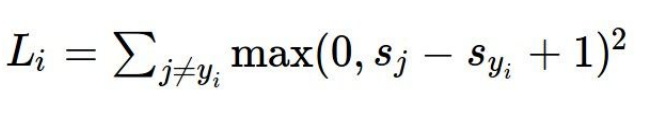
  • 따라서 잘못 예측한 것은 제곱만큼 loss가 커지게 되는 상황이 발생한다. 따라서 데이터의 특성에 따라 극심한 차이를 보고싶을 때 사용한다.

11. 따라서 어떤 loss를 사용하냐는 error값을 얼마나 신경쓰고 있고, 어떻게 정량화 할거냐에 따라 다르다.

12. 아래는 hinge-loss의 example code이다.

    def L_i_vectorzed(x, y, W):
        scores = W.dot(x) # Predict
        margins = np.maximum(0, scores - scores[y] + 1) # Calc Loss
        margins[y] = 0 # class label에 해당하는 것은 0으로 두는 일종의 trick에 해당한다.
        loss_i = np.sum(margins) # Summation Loss
        return loss_i # return
    

Regularization

13. 또다른 질문이 있다. *Loss가 0인 W를 찾았다면 이 값과 동일한 다른 W도 존재하는가?*에 대한 질문이다.

14. 정답은 있다! 이다. 기존 W에 2배를 한다고 해서 Loss는 변하지 않는다. 앞서 loss function이 최적의 W를 찾기 위해 정량적으로 나타내는 것이라고 설명을 했다.

15. 하지만 우리는 수많은 W가 0이 된다는 사실을 방금 알게 되었다. 이는 모순임을 알 수 있다.

16. 왜냐하면 오직 위 식은 data의 loss에만 신경을 쓰고 있기 때문이다. 이때의 data는 xi, 즉 training data이다. 이는 아래 그림과 같이 과대 적합 (Overfitting) 인 문제가 발생한다.

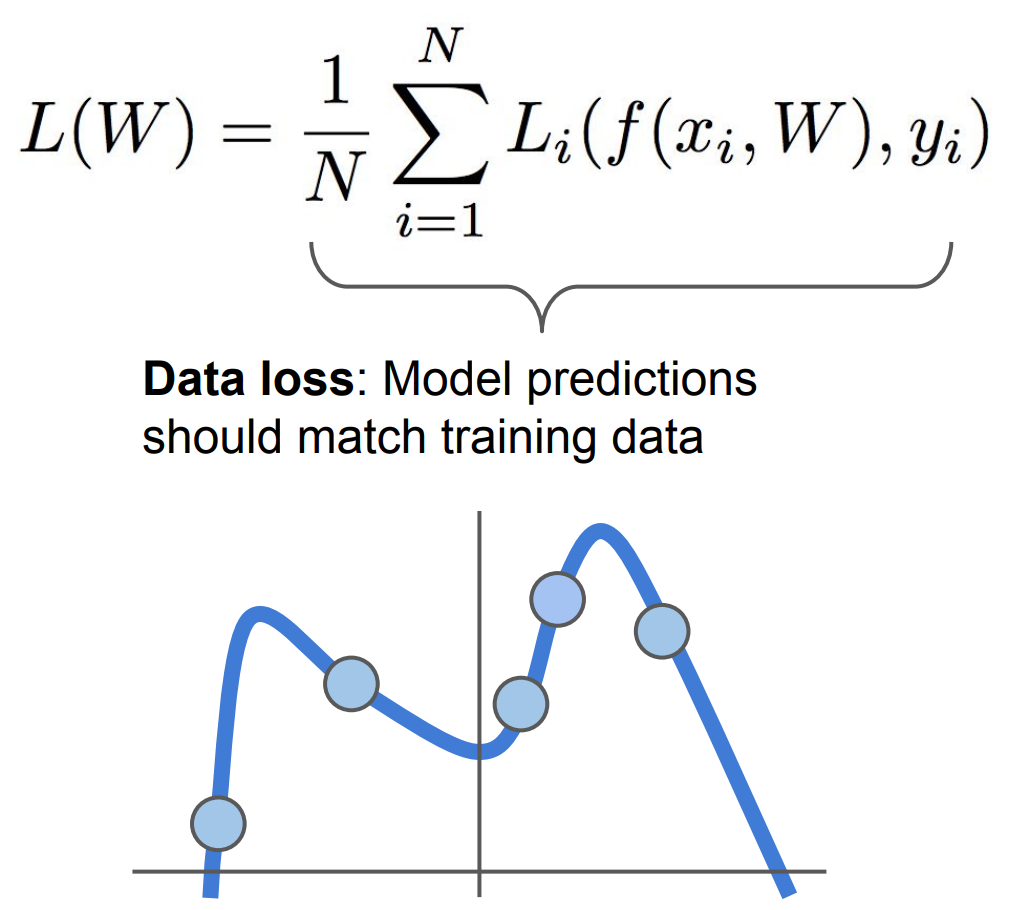
17. 우리는 test data에 대한 performance에 관심이 있지 training data에는 관심이 없다. 따라서 우리는 아래 그림과 같이 되기를 원한다.

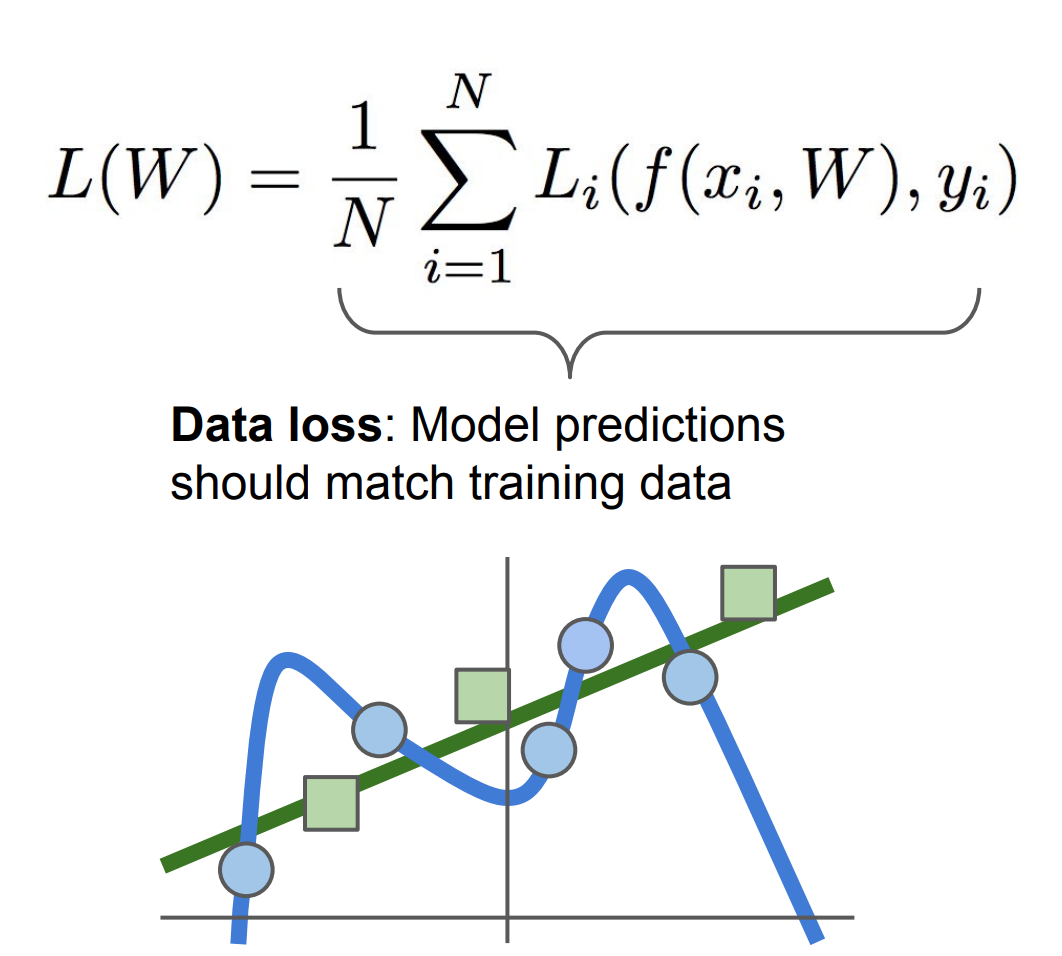
18. 따라서 기존 Loss 식에 변화를 주어야 된다. 기존 식에 Regularization을 추가하여 이 식은 분류기가 더 간단한 W를 선택하도록 패널티를 주는 역할을 한다.

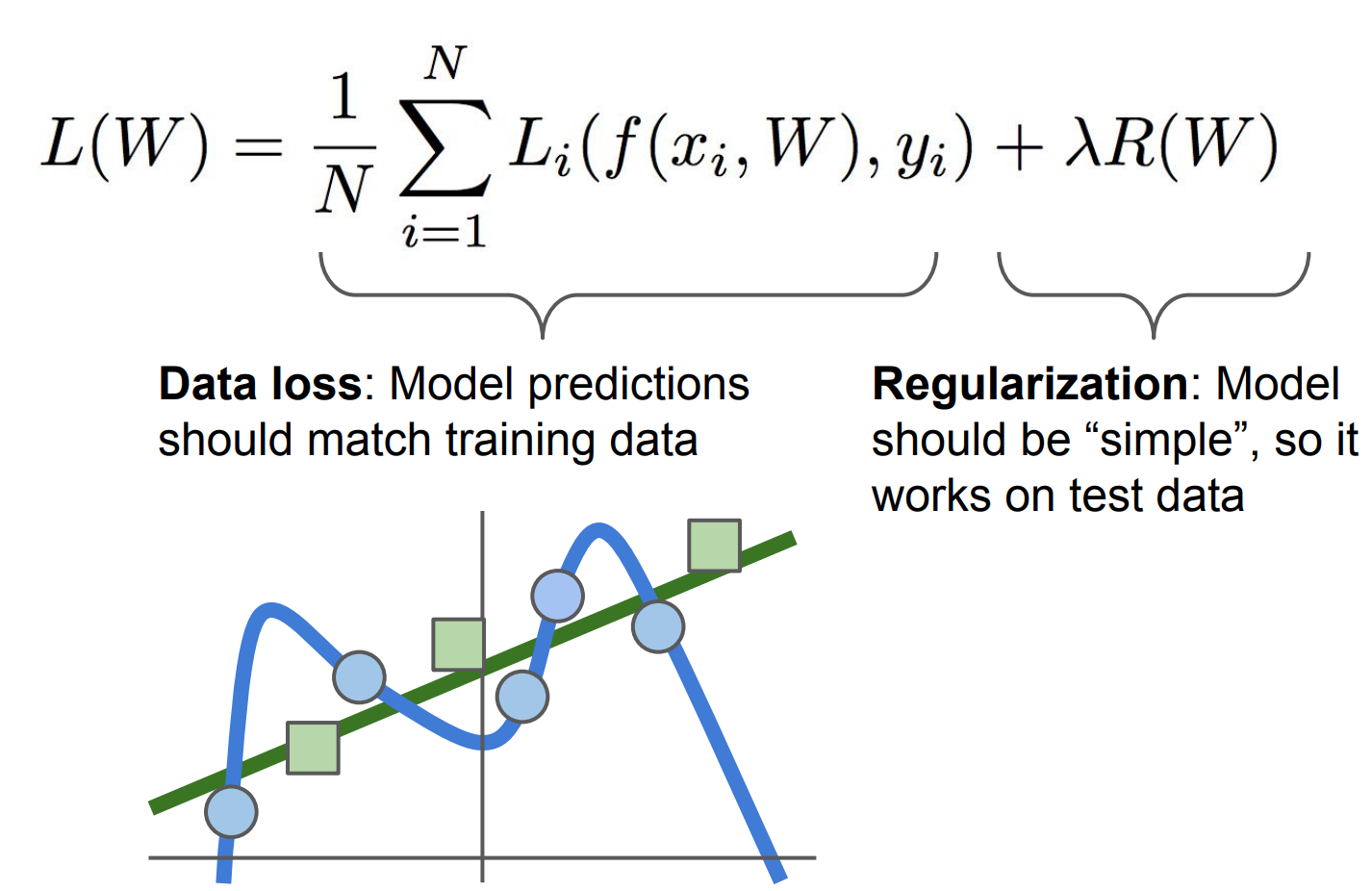
19. 위 식을 볼 수 있듯 더이상 data에 대한 function이 아니라 weight기반의 함수임을 알 수 있다. 이 Regularization에는 L1, L2 Regularization이 있다.

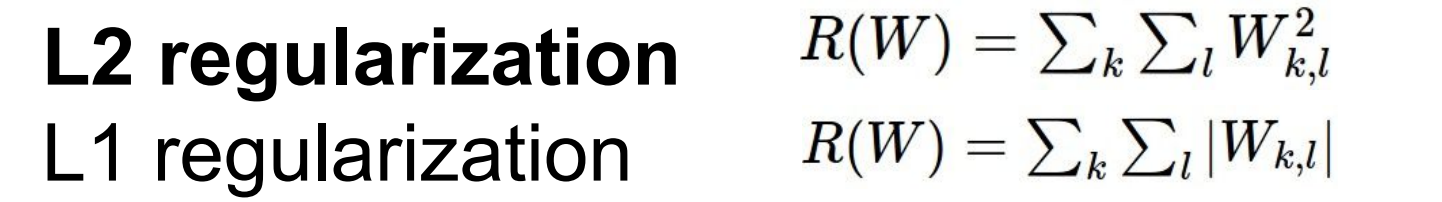
Weight Decay (L2 Regularization)

20. L2를 Weight Decay로도 부른다. L2는 W에 대한 Euclidean Norm이다. 해당 부분은 여기에 있다.

• L2 Norm을 사용하면 L2 Regularization, Ridge Regression 이다.
• L1 Norm을 사용하면 L1 Regularization, Lasso Regression 이다.

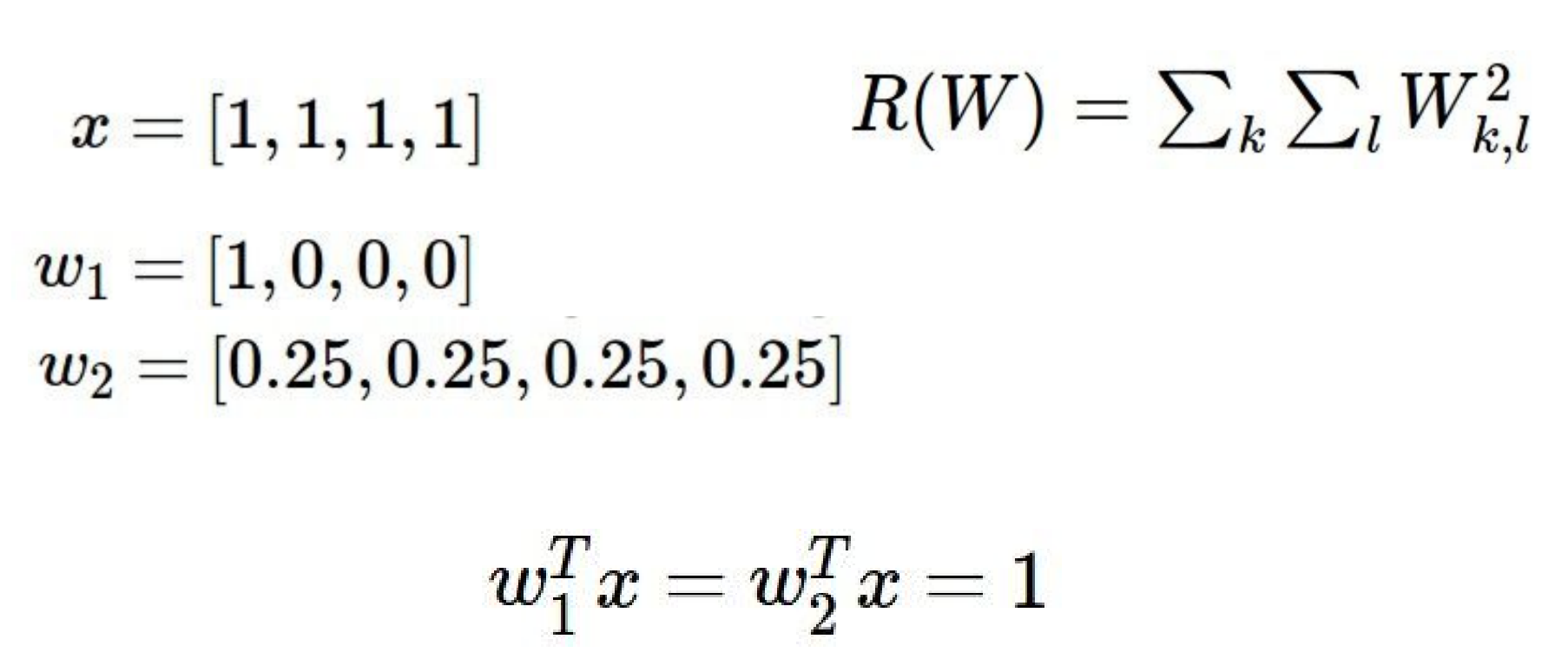
21. 위 같이 결과가 같을 때 L2 Regularization은 어떤 W를 선호 할까? 바로 W2를 선호한다.

22. 이유는 L2는 x의 모든 다른 값에 W의 영향들을 분산시키는 것을 선호한다. 따라서 값이 분산되어있는 W2를 더 선호하게 된다.
    • 따라서 최종 분류기는 모든 입력 차원을 소수의 입력 차원보다 작은 양으로 매우 robust하게 고려하도록 권장된다.
    • 특정 x 벡터에 의존하는 것이 아닌, 전체 x 벡터에 따라 분산되어 의존하기 때문이다.

23. 반면 L1은 0의 개수 즉, 행렬의 Spase한 특징을 선호하여 0의 개수로 모델의 복잡성을 계산한다. 따라서 W1을 더 선호하게 된다.

24. 따라서 L1, L2 등등을 선택하는 것은 데이터의 특성에 따라 다르다.

SoftMax

25. 이전까지 실제 score에 대한 해석은 없었다. 그 점수가 무엇을 의미하는지는 말을 안했다. 이젠 이 score에 대한 해석을 품은 Loss Function에 대해 알아볼 것이다.

26. Softmax는 Multinomial logistic regression이다. 식은 아래 그림과 같다.

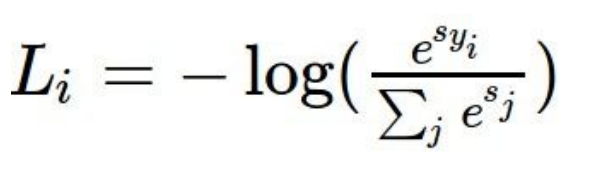
27. 위 식을 보면 score를 전부 이용하고 그것에 지수를 취하여 양수가 되게 만든다. 그리고 그런 지수들의 합으로 정규화를 시킨다. 그렇게 되면 전체 총합이 1인 확률 분포를 얻게 된다.

28. 위에서 얻은 확률이 해당 클래스일 확률을 나타내고 그것을 최대화 하기 위해 log를 씌운 후 Loss Function은 badness를 측정하므로 마이너스로 loss를 표현한다.

29. 다음으로 SoftMax의 2가지의 질문이 나온다.

• Q1: Softmax의 최대값과 최소값은 이론적으로 0, 무한대이다.
  • 정답 class일 때: log(1) = 0, 즉 손실이 0
  • 오답 class일 때: log(0) = 무한대, (자연 상수 e가 0일 때는 -무한대밖에 없으므로 이론적으로 나타낸다.)
• Q2: W가 임의의 초기화 된 작은 값일 때 s가 0이면, log(classes_num)으로 나온다.
  • 이는 debugging시 유용하다.
  • 훈련 시 초기의 loss값이 log(classes_num)이 아니라면 과정 중 어떤 것이 잘못되었는지 다시 볼 필요가 있다.

30. SVM Loss에서는 정답 class의 확률을 조정한다고 해서 loss는 변하지 않았지만 SoftMax는 그렇지 않다. 왜냐하면 SoftMax는 확률을 1로 만드는 것(정확하게 예측하는 것)이 목표이기 때문이다.

31. SoftMax는 정답 score가 충분히 높고, 다른 score가 충분히 낮은 상황에서도 정답 class의 확률을 높이는데 최선을 다할 것이다.

• 이는 성능 개선의 관점에서 차이가 발생한다.

Optimization

32. Optimization의 목적은 loss function을 최소화 시키는 W를 찾아내는 과정이다. 궁극적인 목적은 신경망(NN)을 최적화시키는 것이다.

33. 이런 Optimization의 방법 중 Random Search방법이 있다. 주어진 parameter를 무작위로 넣고 가장 좋은 W를 찾는 방법이다.

bestloss = float('inf')
for i in range(100):
    W = np.random.randn(10,3073) * 0.0001 # Get W randomly
    loss = L(X_train, Y_train, W) # 랜덤 W를 사용해 loss 구하기
    if loss < bestloss: # 최적의 loss 찾기
        bestloss = loss
        bestW = W

34. 대략 10% 정확도로 매우 안좋다고 나온다. 여기서 얻은 아이디어로는 Loop라는 것이다. 조금씩 개선 시키는 방법을 이용할 수 있겠다 라는 점이다.

따라서 무작위로 뽑은 파라미터로 시작해서 반복적으로 조금씩 개선하여 loss를 낮추는 것이다.

35. 이는 마치 산 꼭대기에서 눈을 가리고 산을 내려오는 방법과 같다고 표현을 한다.
    • 언덕의 각 지점에서의 고도가 loss function의 loss이다.

36. 다음 Optimization방법으론 Follow the slope가 있다.

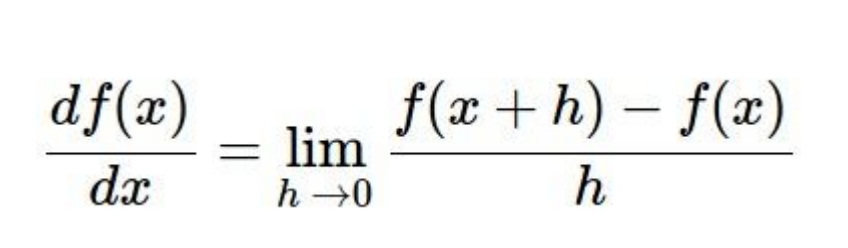
37. 위 식은 미분 식이다. 첫번째 방법처럼 무작위가 아닌 gradient(기울기)를 이용하여 기울기가 가장 가파른 곳을 찾아서 그 단서를 이용해 이동할 수 있다.

38. 1차 함수일 때 어떤 점에서 움직이는 경우의 기울기는 함수의 순간 증가율이다. gradient라는 것은 변수 하나가 아닌 여러개의 경우를 일반화 시킨 것이다.

• Gradient: the vector of (partial derivatives) along each dimension

39. gradient는 두 가지 방법이 있다.

• 수치 gradient
• 해석 gradient

40. 수치 gradient를 사용하면 아래 그림과 같이 모든 차원을 하나씩 돌아가는 오버헤드가 발생한다.

• gradient를 수치적으로 계산하는데 드는 비용은 parameter 수에 따라 선형적으로 증가한다.

41. 위 그림에서 보듯이 h의 값을 임의로 0.0001의 작은 값으로 두었다. 하지만 단순히 작은 h의 값을 사용하기 때문에 계산이 비효율 적이다.

• gradient의 진짜 정의는 h가 0으로 수렴할 때의 극한 값. (여기선 그냥 작은 h값)

42. 따라서 나온 것이 해석적 미분이다. 다음 강의에 나온다.

• 해석적으로 푸는 것이 수치적으로 푸는 것보다 더 효율적이다.

Gradient Descent

while True:
  weights_grad = evaluate_gradient(loss_fn, data, weights)
  weights += - step_size * weights_grad # parameter update
  # step_size == lr(learning rate)

43. 위 식 처럼 우선 W를 임의의 값으로 초기화를 한후, gradient를 계산하고 가중치를 gradient의 반대 방향으로 업데이트 한다.

• 함수가 가장 크게 증가하는 방향의 반대이므로

44. 위 식도 N개의 전체 training set을 한 번 더 돌면서 계산하는 것은 똑같다. 이 과정은 데이터의 크기가 클수록 비효율적이다.

Stochastic Gradient Descent (SGD)

while True:
  data_batch = sample_training_data(data,256) # minibatch 가져오기
  weights_grad = evaluate_gradient(loss_fn, data, weights)
  weights += - step_size * weights_grad # parameter update

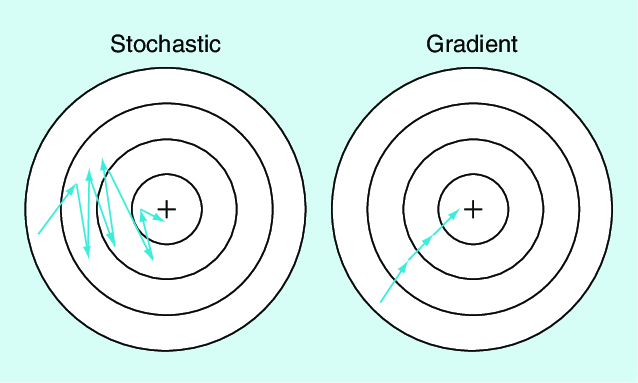
45. 따라서 나온 것이 SGD이다. 작은 training sample 집합으로 나눠서 학습하는 방법이다. **Mini-batch gradient descent(MGD)**이긴 한데 SGD라고 통용된다.

46. Batch만 이용하여 gradient를 구하는 것이다.

• ConvNet을 쓸 때 한 번에 120만개 중 256개 짜리 배치만 이용해서 parameter 업데이트를 한다.

Reference

• https://chasuyeon.tistory.com/entry/CS231n-3강-정리-Loss-Functions-and-Optimization