[CS231n] 02.Image Classification
Contents
개요
CS231n을 공부하면서 정리를 위해 글을 작성해보려고 한다.
- 1강의 내용은 컴퓨터 비전에 대해 전반적인 역사, 이 course를 통해 얻게 될 내용들에 대해서 소개를 해주었다. 따라서 따로 정리할 것은 없어서 정리하지는 않았다.
The Problem
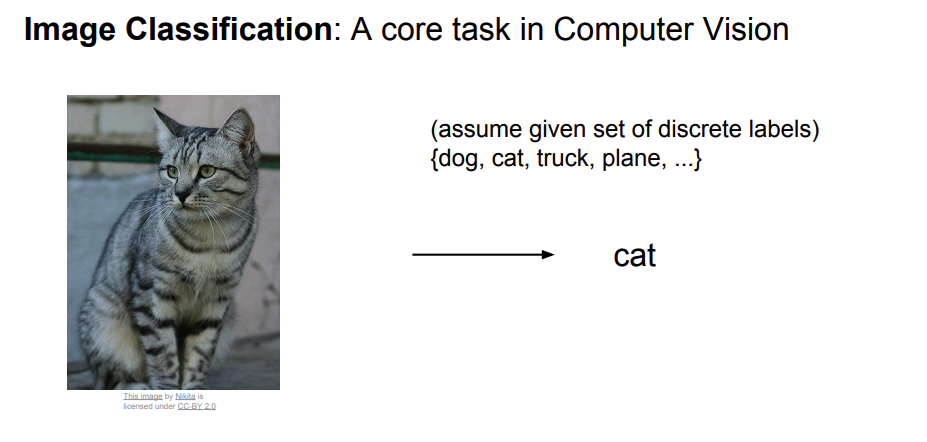
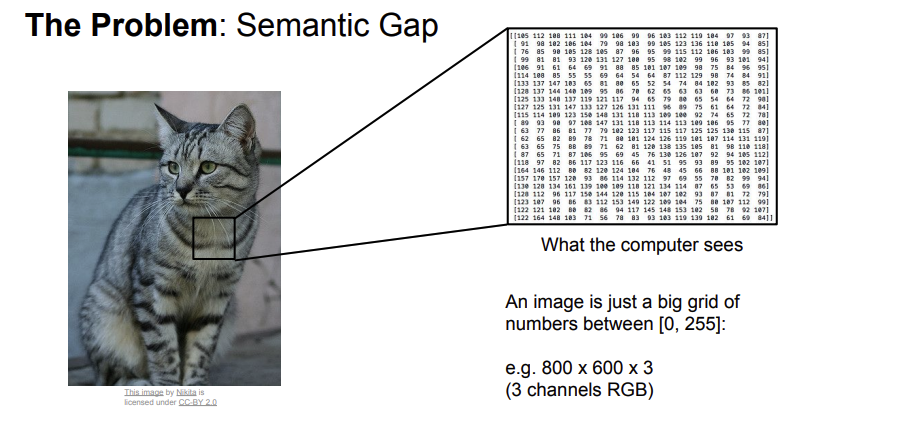
- 컴퓨터는 사람과 달리 이미지를 숫자로 인식을 한다. 따라서 사람이 의미하는 것과 컴퓨터가 이해하는 것에는 차이(Semantic Gap)가 있기 마련이다.
- 또한 컴퓨터가 image를 인식할 때 여러 문제(problem)들이 발생하게 된다.
- Viewpoint variation (카메라의 움직임)
- Illumination (색상 차이)
- Deformation (다양한 모습)
- Occlusion (부분적으로 물체 보이는 현상)
- Background Clutter (배경 혼란 현상)
- Intraclass variation (다양한 종류)
- 따라서 우리는 이런 problem들을 극복할 수 있는
robust하고확장성이 뛰어난 모델을 만들어야 한다.
- 이런 모델들을 만들기 위해서
Data-Driven Approach(하나의 접근 방식)를 제안한다.
-
Data-Driven Approach에 대해서 아래에 설명을 작성했다.
- image와 label들의 dataset을 모은다.
- 간단한 분류기를 machine learning에 의해 훈련킨다. (함수에서 train)
- 새로운 이미지를 가지고 분류기를 평가한다. (함수에서 predict)
Nearest Neighbor
- 이 방법은 학습 데이터와 새로운 이미지들을 비교해서 학습 데이터 중에서 가장 유사한 이미지로 레이블을 예측하는 방법이다.
Nearest Neighbor에서 이때 유사한 이미지로 판단하기 위해서L1(manhattan) distance가 있다.
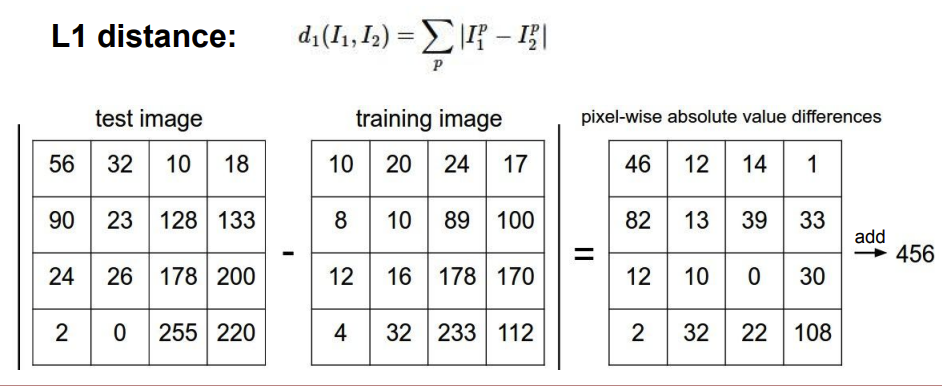
L1 distance는 새로운 이미지의 pixel에 학습 데이터를 뺀 절대값들의 합을 구하여 그 합들이 가장 최소로 나온 이미지를 유사하다고 판단하는 방법이다.
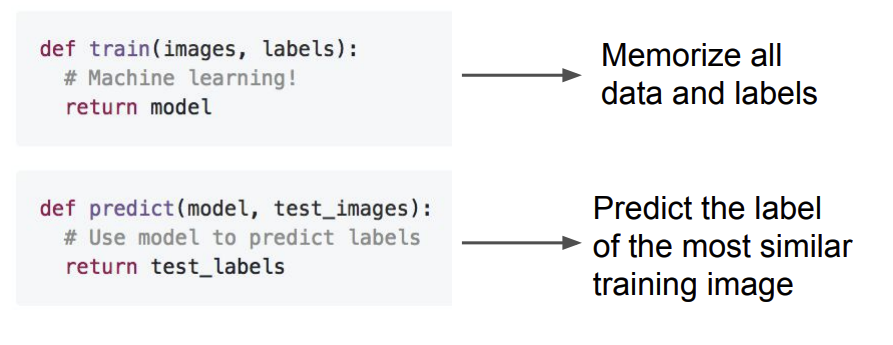
- 위 그림과 함께
Nearest Neighbor의 과정을 보자면 train 과정에서 모든 훈련 데이터를 저장한다. 그리고 predict 과정에서 모든 훈련 데이터를 비교하여 가장 유사한 훈련 데이터 image를 찾게 된다.
- 이 과정에서
train: O(1),predict: O(N)(# of iunput)의 시간 복잡도를 가지게 되는데 이것은 잘못되었다고 표현을 한다.
- 왜냐하면 우리는 보통 분류기가 빠르게 예측하기(predict)를 원하지만 Nearest Neighbor에서는 그것이 반대가 되어있는 것을 알 수 있게 된다.
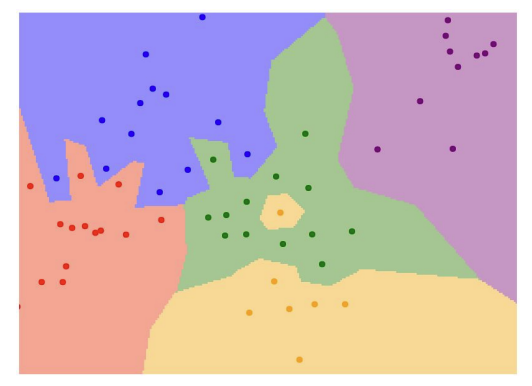
- 또한
Nearest Neighbor알고리즘은 가장 가까운 이웃만을 보기 때문에 위와 같은 초록색이 대부분인 영역에서 노란색을 예측하는 문제가 발생 할 수 있다. 따라서K-Nearest Neighbor알고리즘이 나오게 된다.
K-Nearest Neighbor
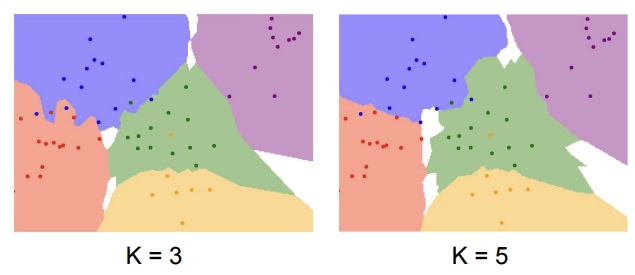
- 그 다음으로 가까운 Neighbor을 K개의 만큼 찾고, 그것끼리 다수결의 결정으로 예측을 하는
K-Nearest Neighbor방법이 있다.
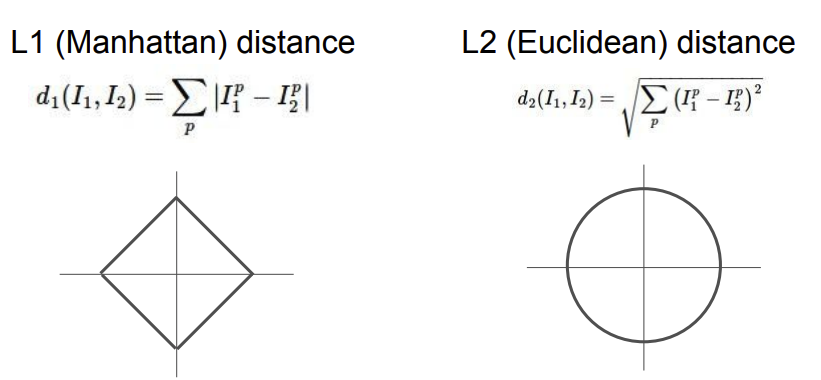
- 또 이때 유사도를 결정할 때
L1 distance가 아닌L2(Euclidean) distance의 계산식이 있다.
- 이것은 L1과 달리 좌표계가 무엇이든 상관이 없지만 L1의 경우에는 좌표계에 따라 계산값이 변할 수 있다.
- 각각 어떤것이 좋은지는 데이터의 성격에 따라 다르다
- input 데이터가 각각의 항목이 중요한 성격(salary, 성별, 연봉 등)을 가진다면
L1이 적당할 수 있지만 - 어떤 역할인지 상관이 없으면
L2가 더 좋을 수 있다.
- 위
그림 2를 보게 되면 K가 커질 수록 좀 더 경계들이 부드러워지는 모습을 볼 수 있게 된다. 그렇다면 K가 무조건 커지면 좋은 것이냐? 그건 또 아니다. 이때 중요한 것이 적절한 K를 결정하는 것이 중요하다.
- 이런 K같은 요소들을
Hyperparameter이라고 부르고 다음으로 이런 적절한Hyperparameter을 선택하는 방법에 대해서 설명하겠다.
Hyperparameter
- 이런
Hyperparameter는 직접 시도해보고 가장 좋은 값을 찾는 것이 정답이다.
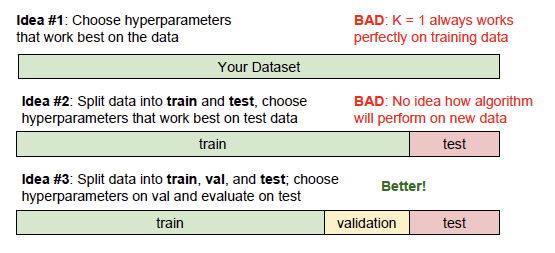
-
idea #1:학습데이터만을 학습하여 하이퍼 파라미터를 선택 -
idea #2:train한 모델을 바탕으로 Test set에서만 잘 동작하는 하이퍼 파라미터를 선택 -
idea #3:train set으로 모델을 학습, validation set으로 가장 좋았던 하이퍼 파라미터 선택, validation set에서 고른 하이퍼 파라미터를 바탕으로 test set을 test시작
- 따라서 이런 적절한
Hyperparameter가 무엇인지 결정할 때 위 3개의 방법 중idea #3방법이 제일 좋다. 왜냐하면idea1,2는 unseen data에 대한 정확도가 떨어진다. 결국idea #2도 새로운 data에 약한 특성을 보인다.
- 예를 들어,
idea #2일 때 K값을 바꿔가면서 이 중 가장 높은 성능을 지닌 K를 정한다고 했을 때 이는 test데이터에 좋은 성능을 보이는 K값인 것이다. 다른unseen data에 좋은 결과값을 보여줄 지는 모르는 것이다.
- 따라서 모델 훈련 중 아예 안보이는 unseen data를 설정하는
idea #3가 제일 좋은 방법이다.
- 이때 Validation에서 이 알고리즘이 잘 작동하고 적절한 K를 사용하는지 판단하고 그 값들을
unseen data로 활용하는 방법이다.
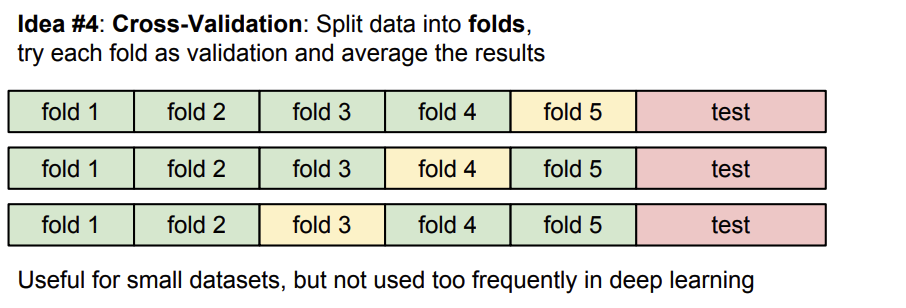
- 세가지 방법과는 다르게 네번째 방법으로
Cross-Validation방법이 있다.
- 전체 dataset을 여러 개의 fold로 나눈 후 그 중 하나를
validation set으로 두고 나머지를 훈련 데이터로 사용하여 폴드를 나눌 때마다retrain과정을 거쳐 최적의 파라미터를 찾는 방법이다.
- 지금까지의 idea중 가장 일반화를 잘 한다.
- 하지만, 작은 dataset에서는 자주 사용하지만 dataset 크기가 큰 deep-learning에서는 사용하지 않는 방법이다.
- 큰 dataset을 fold 수 만큼 다시 학습을 돌려야 하는 문제가 발생하기 때문이다.
NN nerver used on image
- 결론적으로
NN알고리즘은 image에서는절대 사용하지 않는다.위에 언급한predict과정이 시간이 오래 걸린다는 것과L1, L2등으로 구한 pixel간의 유사도 (distance 유사도)가 의미있는 값이 아니기 때문이다.

- 위 그림을 보면 3개의 image는 원본 image와 분명히 육안으로 다르지만 L2 distance가 같게 나온다. 이를 통해 의미있는 값이 아님을 알 수 있게 된다.
-
또한 차원의 저주(curse of dimentionality)문제가 있다.
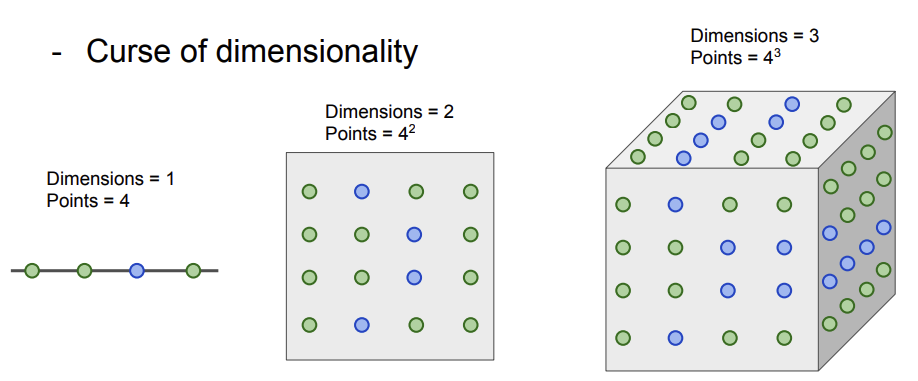
-
K-NN이 잘 동작하기 위해서는 전체 공간을 조밀하게 커버 할 만큼 충분한 훈련 샘플들이 필요하게 된다. 하지만 이런 데이터 충분하지 않으면 이웃들 간의 거리가 멀 것이라고 예측하고 제대로 된 분류를 하지 못한다.
- 차원이 증가함에 따라 기하급수적으로 데이터가 필요하게 될 것이고 그만큼 데이터를 모으는 일은 어려울 것으로 예상이 되기 때문에 NN은 image에서 사용되지 않는다.
Linear Classification
Linear Classification이란 기본 블럭들을 빌딩의 층처럼, 레고를 쌓는 것들의 과정이라고 생각하면 된다.
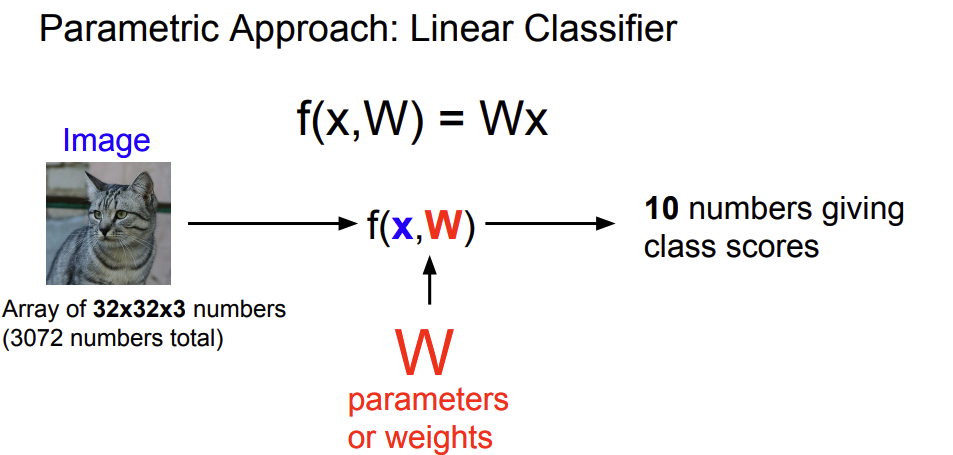
Linear Classification에서는Parametric Approach를 사용하게 된다. 이것은 앞선KNN에는 parameter가 없지만Linear Classification에서는W,b라는 parameters들이 존재하게 된다.
- 따라서 우리는 이
W,b를 훈련 과정 동안 업데이트를 할 것이고 훈련 시간에 training data가 필요가 없게 된다.
KNN보다 효율적인 것을 확인이 가능하다.
- b는 편향(Bias)값이다. 이때 이 편향은 데이터와 무관하게 특정 클래스에 어떠한
우선권을 부여하게 된다.
- dataset이 imbalace인 상황에서 특정 class에 우선권을 더 부여하기 위함
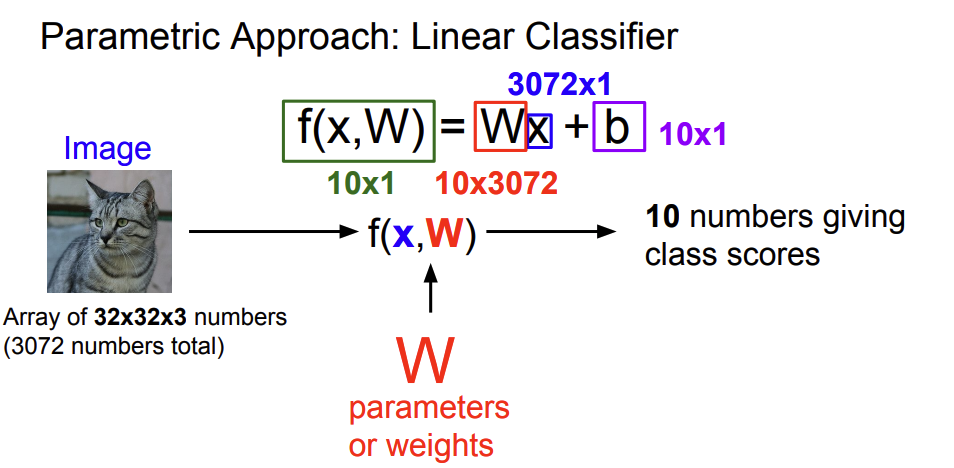
그림7을 보면 input image size가 2*2일 때 각 성분(x,b,…)의 크기를 나타난다.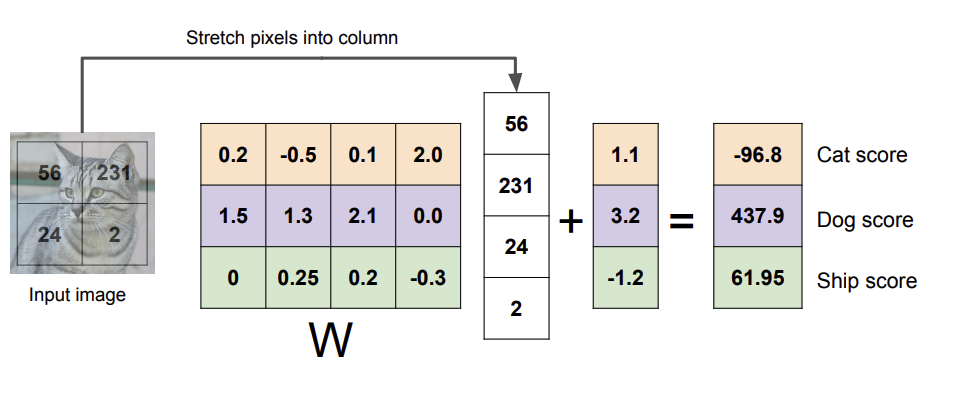
- 연산은 단순한 행렬과 벡터의 곱(mat mul)임을 알 수 있다.
- 이때 W에서 각 row는 하나의 클래스를 담당하므로 이를 템플릿으로 볼 수 있게 된다.
- W의 행 벡터와 input data의 열 벡터 간의 내적을 계산하게 되는데 이는
각 클래스 간 템플릿의 유사도를 의미하는 것으로도 볼 수 있게 된다.

- 따라서 위 그림이 각각의 Weight의 템플릿 값들을 시각화 한 것이고 이를 통해 모델이 데이터를 이해하기 위해 어떤 학습을 하는지 확인이 가능하다.
- 이 weight값은 각 class에 있는 모든 이미지를 평균화 시키므로 각 class에 있는 모든 훈련 데이터의 모습을 포함하게 된다.
- 따라서 말(horse)를 보면 데이터 상에 말의 머리가 왼쪽, 오른쪽 모습이 모두 있을 수 있는 것이 확인 할 수 있게 된다.
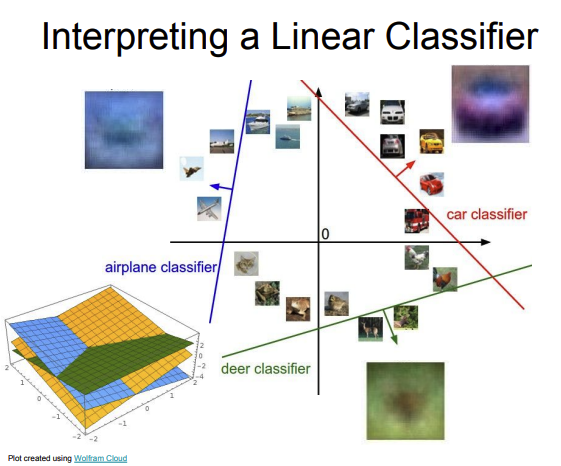
- 또한
Linear Classification에서 이미지를 고차원에서 data point상에서 하나의 점으로 생각하는 것이다.
- 각 class는
linear dicition boundary를 가지며 이러한 선을 기준으로 image를 분류하는 것이라고 생각하면 될 것 같다.
- 하지만 이렇게 선분으로 구분하는
Linear Classification는 풀 수 없는 어려운 경우가 존재할 수 있게 된다.
- Data들을 binary의 선분으로 구분할 수 없을 경우 바로 이러한 문제가 발생하게 된다.
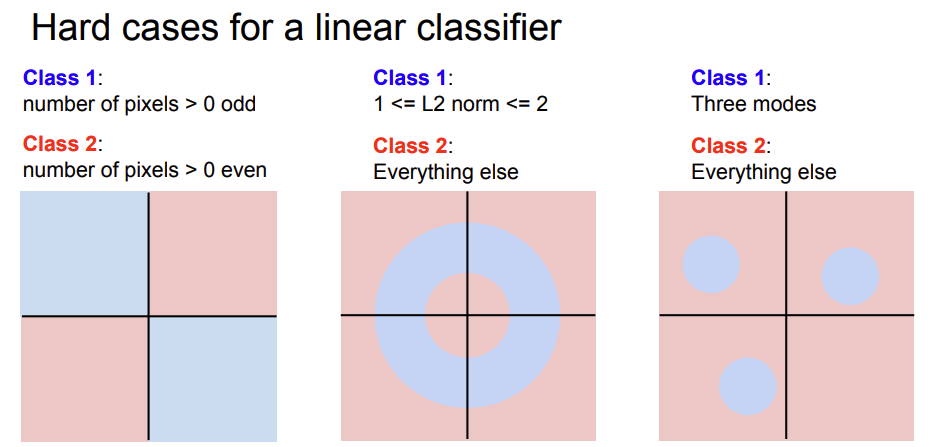
- 위 그림을 보면
Xor,Donut,Multimodal problem들은Linear Classification으로 분류 방법이 없다.
- 하나의 선분으로 data간의 class를 구분할 수 없다는 뜻이다.
- 이것의
Linear Classification의 한계이다.
- 마지막으로
Linear Classification을 사용하면NN알고리즘들과 달리 Train 시간은 O(N), Test 시간은 O(1) 이 걸려 우리가 원하는 시간을 나타낼 수 있다.